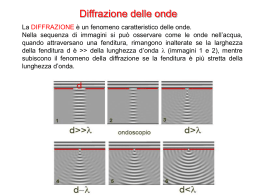
La diffrazione
Curvatura dei raggi luminosi quando oltrepassano un ostacolo di dimensioni a   (Grimaldi, 
1650). La figura di diffrazione è formata da figure di interferenza.
Fresnel nel 1819 dimostrò sperimentalmente che le figure di diffrazione possono essere spiegabili
nell’ambito della teoria ondulatoria della luce (la macchia di Fresnel).
Normalmente si seguono due approcci:
Diffrazione di
Fraunhofer
Sorgente e schermo
sono posti a GRANDE
DISTANZA
dall’apertura
diffrangente

Si ottiene con l’utilizzo
di LENTI

Fronti d’onda piani,
raggi paralleli

Semplicità di calcolo
Lezione n. 16
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
Diffrazione di
Fresnel
Sorgente e schermo
sono posti a
DISTANZA FINITA
dall’apertura
diffrangente

Fronti d’onda NON
piani, raggi NON
paralleli

Difficoltà di calcolo
1
Diffrazione da una singola fenditura
Si consideri un’onda piana () diffratta da una fenditura di ampiezza a. Si vuole trovare la posizione
del primo minimo (frangia scura). Per questo motivo, consideriamo la fenditura come suddivisa in
due metà ideali (a/2). Il raggio luminoso proveniente da uno dei due bordi della fenditura
interferisce con il raggio proveniente dal centro. Se P1 è la posizione della prima frangia scura, si ha
interferenza distruttiva se la differenza di cammino ottico tra i due raggi (a/2 sin q) è pari a /2. Tale
soluzione è tanto più accettabile quanto più lo schermo C è distante dalla fenditura.
Pertanto, la posizione del primo minimo si trova a a sin q = 
Lezione n. 16
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
2
La posizione dei minimi
Per trovare la posizione del secondo minimo (frangia scura), consideriamo ora la stessa fenditura
come divisa in 4 quarti (a/4). In questo caso, la differenza di cammino ottico tra due coppie di raggi
adiacenti (r2-r1, r3-r2, r4-r3) cioè a/4 sin q, deve sempre essere pari a /2. Di nuovo, tale soluzione è
tanto più accettabile quanto più lo schermo C è distante dalla fenditura.
Pertanto, la posizione del secondo minimo si trova a
a sin q = 2 
Per analogia, la posizione del minimo m-esimo si troverà a
a sin q = m 
Lezione n. 16
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
3
Differenze di fase
Suddividendo la fenditura in tantissimi sottointervallini, è possibile analizzare il contributo di ogni
intervallino supponendo che esso si comporti come sorgente elementare puntiforme di un fronte
d’onda (principio di Huygens). Analizziamone il comportamento su uno schermo posto a grande
distanza partendo dalla posizione centrale e muovendoci verso angoli q crescenti..
Nella posizione centrale (q=0) tutti i fasori (vettori di fase) sono paralleli perché hanno la stessa fase
(il cammino ottico è per tutti lo stesso). Pertanto (caso a) l’ampiezza dell’onda risultante Eq, data
dalla somma vettoriale di tutti i fasori, è massima (=Em).
In una posizione generica q (caso b) i fasori si sommano vettorialmente generando un fasore
risultante di ampiezza Eq < Em.
Quando i fasori formano una linea chiusa (caso c), il fasore risultante ha ampiezza nulla (Eq=0) e tale
angolo corrisponde al primo minimo.
Proseguendo nel muoversi sullo schermo, l’ampiezza del fasore risultante ricomincia a crescere (caso
d) fino ad arrivare al secondo massimo ecc.
Lezione n. 16
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
4
Intensità dell’onda diffratta
Nel caso di una posizione generica q, i fasori si sommano vettorialmente
generando un fasore risultante di ampiezza Eq < Em.

E
Essendo Eq  2 R sin ed anche   m
si arriva all’espressione:
R
2
Eq 
Em

2
dove
sin 
2 oppure, introducendo l’intensità:


2

a
sin q

 sin 

2
Iq  I m 
 
2



 sin  
  Im   




I minimi si hanno per =m
con m=1,2,3,…
La larghezza centrale del
massimo
di
diffrazione
diminuisce
al
crescere
dell’ampiezza della fenditura
rispetto a .
Lezione n. 16
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
5
Diffrazione attraverso un foro circolare
L’immagine prodotta da un foro circolare di diametro d produce figure di diffrazione. Il primo
minimo si trova alla distanza angolare data dalla formula seguente, dove 1.22 è il risultato
dell’integrazione delle sorgenti elementari in cui si può suddividere l’apertura circolare.




sin q  1.22
q R  arcsin 1.22   1.22
d
d
d

qR può anche essere visto come l’angolo minimo affinché 2 oggetti siano separabili (criterio di
Rayleigh).
Per q > qR i due oggetti sono SEPARATI
Per q > qR i due oggetti sono NON SEPARATI
Lezione n. 16
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
6
Diffrazione da doppia fenditura
Nel caso in cui luce di lunghezza d’onda  passi attraverso tante fenditure di larghezza a<<, le
frange di interferenza hanno tutte la stessa ampiezza (caso a). Se, invece, la fenditura ha ampiezza
a, le frange di interferenza sono modulate dalla figura di diffrazione (b) e l’ampiezza risultante
sullo schermo è composta da frange d’interferenza di ampiezza variabile modulata dalla figura di
diffrazione (c).
sin 2 
Intensità risultante
Intensità
Iq  I m, DIF 2
Intensità
I q  I m, INT cos 2 

sin 2 
diffrazione
Iq  I m,DIF 2 cos  
a
interferenza    d sin q
  sin q



Lezione n. 16
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
7
Reticoli di diffrazione
Un insieme di N fenditure uguali, parallele ed equidistanti è chiamato reticolo di diffrazione (es.: gli
atomi in un solido cristallino come NaCl).
Come visto prima, quando si aumenta il numero di fenditure, si ottiene una figura con un insieme di
frange di interferenza, le cui intensità sono modulate dall’inviluppo di diffrazione. Nel caso in cui
tale numero sia molto grande, il massimo centrale di diffrazione (per ogni fenditura) è molto stretto,
e si creano strette frange di interferenza.
La posizione dei massimi è data dall’equazione:
dove d è la distanza tra
due fenditure adiacenti.
Solitamente, si usa caratterizzare i reticoli di diffrazione con il passo, cioè il numero di fenditure per
unità di lunghezza (ad es.: 600
fenditure per mm).
d sinq  m
Lezione n. 16
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
8
Larghezza delle righe nei reticoli
I reticoli di diffrazione sono solitamente usati per misurare lunghezze d’onda. La loro principale
caratteristica è la larghezza delle righe (spettrali).
Si definisce larghezza di riga la distanza angolare tra la posizione centrale ed il punto in cui
l’intensità va a zero.
Il primo minimo (di diffrazione) per una fenditura singola cade nel punto in cui la differenza di
cammino ottico (a sinq) vale . Per un reticolo con N fenditure e passo d, la differenza di cammino
ottico è N d sin Dq  N d Dq . Tale valore deve essere pari a . da cui Dq   / N d

Se la fenditura si trova, invece, ad un angolo rispetto all’asse centrale, tale valore è: Dq 
Nd cos q
Pertanto la larghezza di riga è migliore per reticoli più fitti.
Lezione n. 16
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
9
Lo spettroscopio
Come noto, ogni sostanza emette onde elettromagnetiche con uno spettro caratteristico. Per le
sostanze gassose, normalmente lo spettro di emissione è composto da righe spettrali.
Uno spettroscopio a reticolo permette di osservare l’intensità delle righe spettrali che escono dal
reticolo G colpito dalla luce della sorgente S focalizzata attraverso le lenti L1 e L2 e la fenditura S1
orientando semplicemente il telescopio T (cioè variando l’angolo q).
La riga spettrale osservata quando
l’angolo vale q=0 contiene tutte le
. Invece, a causa della
dispersione, i massimi di ordine m
successivo delle varie righe
spettrali si osservano a posizioni
angolari qm distinte.
Lezione n. 16
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
10
Dispersione e potere risolutore nei reticoli
In un reticolo la capacità di distinguere due lunghezze
d’onda molto vicine tra loro è una caratteristica
fondamentale. Tale proprietà è fisicamente esprimibile
attraverso la dispersione, data da:
Dq
m
D

D d cos q
Dq = distanza angolare tra le due righe
D = differenza di  tra le righe
Maggiore
d = passo del reticolo
m = ordine del massimo
potere risolutore
Una grandezza fisica alternativa è il potere risolutore di
un reticolo, definito dall’espressione:
R

 Nm
D
Lezione n. 16
N = numero di fenditure
Maggiore
dispersione
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
11
Diffrazione dei raggi X
I raggi X hanno   0.1 nm  10-10 m e pertanto un reticolo di diffrazione
che funzioni nel visibile (  550 nm  5.5 10-7 m ) non ha il potere
risolutore sufficiente per discriminare le  dei raggi X.
Ma quando un fascio di raggi X colpisce un solido cristallino, i raggi
vengono diffusi dal cristallo stesso in tutte le direzioni. In alcune direzioni
le onde diffuse interferiscono positivamente, in altre negativamente, per
cui si creano massimi in corrispondenza di piani di riflessione paralleli.
Le condizioni (legge di Bragg) per cui ciò avviene sono: 2d sinq = m
In questo caso la relazione tra distanza
interplanare d e dimensione della celle
elementare a0 vale 50.5 d = a0
Un metodo per generare raggi X è quello di riscaldare
un filamento incandescente F i cui elettroni, accelerati
dalla d.d.p. V, colpiscono un bersaglio metallico T posto
dentro un tubo a vuoto C.
Lezione n. 16
Corso di Fisica B, C.S.Chimica, A.A.
2001-02
12