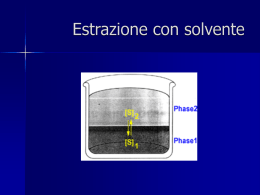
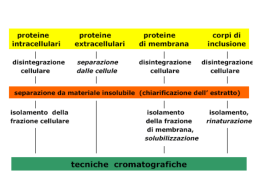
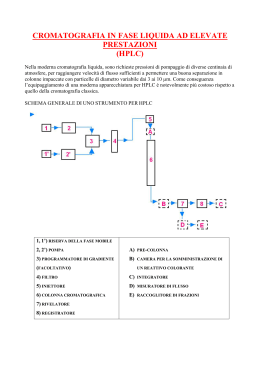
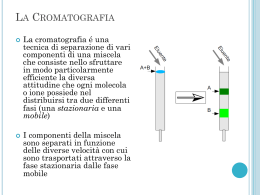
Cromatografia
Fabrizio Papa
Simulazione di
una
Cromatografia
Poniamoci alcune domande:
1) Perché da una sostanza verde abbiamo ottenuto due sostanze, una gialla ed una blu?
2) Perché le due sostanze sono scese verso il basso?
3) Perché le due sostanze si sono separate?
4) Perché il volume occupato dalle sostanze è aumentato?
5) Perché la sostanza blu più trattenuta occupa un volume maggiore della sostanza
gialla meno trattenuta?
Un esempio
Cerchiamo ora di individuare gli elementi della simulazione cromatografica
e dell’esempio dei tipi chiacchierone e riservato ed abbinarli tra loro.
Simulazione
Tubo di vetro
Sostanza blu
Sostanza gialla
Solido
Solvente
Esempio
Tipo Violetto riservato
Corso
Folla
Gambe
Tipo rosa chiacchierone
Cerchiamo ora di rispondere ad una domanda più difficile:
Perché le bande si allargano?
Per rispondere a ciò riprendiamo ancora l’esempio dei tipi chiaccherone e riservato.
Perché si allarga la banda? Un esempio.
1
1
2
2
3
Intensità
Cromatogramma
3
2
1
Tempo
Non resta che cercare dei termini più appropriati per identificare gli elementi e
gli eventi osservati e avremo definito tutto sulla cromatografia.
Tubo di vetro
Colonna cromatografica
Solido
Solvente
Trascinamento del solvente
Sostanze
Fase stazionaria
Eluente: fase mobile
Eluizione
Soluti
Intensità
Tempi di ritenzione
tR
= tempo di ritenzione
t’ R tempo di ritenzione corretto
K’ = (tR – t0)/t0
Fattore di capacità
Kd = Cs/Cm
Coefficiente di distribuzione
t0
K’ = Kd*Vs/Vm
Tempi
Analizziamo ora l’ampiezza della banda:
Intensità
tR
= tempo di ritenzione
W1/2
H
H1/2
W
Tempo
Analizziamo ora in maniera più scientifica perché la banda si allarga:
Percorsi multipli
Diffusione longitudinale
Fase mobile
Fase stazionaria
In fase stazionaria
Trasferimenti di massa
In fase mobile stagnante
Diamo dei valore ai tre contributi che influiscono
sull’allargamento della banda
Percorsi multipli =
Diffusione longitudinale =
A
B
Trasferimento di massa
=
O raggiungimento dell’equilibrio
C
HETP = A + B/v + C*v
v = flusso
Equazione di Van Deemter
HETP = altezza del piatto teorico
lunghezza della colonna = L
n = L / HETP
n = numero dei piatti teorici
Un po’ di statistica
Esempio:
Una fabbrica produce dei prodotti (compresse) con 5 mg di principio attivo (caffeina)
Vi chiedono di verificare se le compresse prodotte contengono effettivamente 5 mg di caffeina
ed in caso contrario di valutare la variabilità.
E voi cosa fate?
1) Le analizzate tutte?
2) Ne prelevate un po’ in modo casuale e le analizzate?
Ne preleviamo 5 che danno il peso di 3, 4, 5, 6, 7
Media =
3+4+5+6+7
=5
5
La media non ci dice nulla sulla variabilità
Proviamo con gli scarti dalla media
3 – 5 = -2
4 – 5 = -1
5–5= 0
3 – 5 = (-2)2
4 – 5 = (-1)2
Eleviamo al quadrato
5 – 5 = (0)2
6–5= 1
6 – 5 = (1)2
7–5= 2
7 – 5 = (2)2
somma 0
somma
Quello che abbiamo ottenuto si chiama Devianza
10
Dividendo per il numero dei campioni o osservazioni o meglio
per i gradi di libertà ci avviciniamo alla variabilità del singolo campione
10
5-1
= 2,5
Abbiamo appena ottenuto la Varianza
Avendo prima elevato al quadrato ora possiamo fare l’operazione
inversa con la radice quadrata
2,5
= 1,58
Abbiamo finalmente ottenuto la Deviazione Standard
Riprendiamo i numeri appena analizzati
3, 4, 5, 6, 7
Un campionamento di cinque non è molto serio
Facciamo un campionamento di 100 numeri approssimando i pesi a 0,5
Distribuzione dati
Grafichiamo i dati su un istogramma
25
20
Distribuzione di Gauss
15
Serie1
Poli. (Serie1)
La deviazione standard in una curva di
Gauss è cade nel punto di flesso
10
5
La somma delle osservazioni tra –s e +s
risulta essere il 68,2%
0
Serie1
3
3,5
4
4,5
5
5,5
6
6,5
7
1
4
12
21
24
21
12
4
1
Ancora un piccolo esempio:
Due ditte producono due diversi prodotti:
1) Ha una media di 10 e s 2
2) Ha una media di 100 e s 2
Ci chiediamo qual è la ditta che lavora meglio, ovvero è più precisa,
ovvero richiamando un termine cromatografico è più efficiente?
La deviazione standard è uguale
Proviamo a rapportare la deviazione standard alla media
2/10 = 0,2
Se moltiplichiamo per 100 otterremo 20 e 2 ovvero il
Coefficiente di Variazione Percentuale o CV%
2/100 = 0,02
Questo ci dice chiaramente che la ditta che lavora meglio è la seconda
s/ tR
I valori di questo rapporto sono molto piccoli, prendiamo il reciproco
tR/s
O ancora meglio il suo quadrato
(tR/s)2
N = (tR/s)2
1 deviazione standard equivale ad un’ampiezza di picco misurata a 0,882
di altezza, non facile da prendere e quindi si misura alla base che equivale a 4
deviazioni standard o a metà altezza che corrisponde a 2,354 s
N =(tR/Wb
/4)2
N =(tR/h1/2/2,354)2
N = 16(tR/Wb)2
N = 5,545(tR/h1/2)2
Equilibrio?
Kd = Cs/Cm
Kd = [fenolo]s/[fenolo]m
Solvente = etile acetato
Solido = silice
Soluto = fenolo
Estrazione con imbuto
separatore, un processo
all’equilibrio
Kd = Cm/Cs
Kd = [fenolo]H2O/[fenolo]CH2Cl2
La cromatografia non è un processo all’equilibrio
Proviamo a riportare su grafico i tre contributi che tendono ad allargare
una banda cromatografica
HPTE
C
B
A
v = flusso
La cromatografia ci permette di separare due o più sostanze
Abbondanza
Risoluzione
tR
Ancora sulla risoluzione
Cattiva risoluzione
Buona risoluzione dovuta
all’efficienza della colonna
Buona risoluzione dovuta
alla selettività della
colonna
Risoluzione
t r1
Dt
t r2
R = 2 Dt/(W2 + W1)
W1
W2
Efficienza
Particelle di silice
Bande lungo la
colonna
Cromatogrammi
Selettività
Cambiando la fase stazionaria
Cambiando la fase mobile
K’ = tR – t0 / t0
Kd = Cs / Cm
Soluto A
KdA
Soluto B
KdB
A
Fase mobile
Fase stazionaria
Cambiano i tempi di ritenzione
B
Parliamo di tipi diversi di cromatografia
Classificazione in base alla fase mobile
Liquida
Gassosa
Cromatografia su strato sottile
in colonna, HPLC
Gascromatografia in colonna
A fluido supercritico
Tra la cromatografia liquida e la
gascromatografia, in colonna
Cromatografia di assorbimento
Fase mobile
Siti attivi
Fase stazionaria (solido)
Un esempio di cromatografia di adsorbimento (fase inversa)
Silice (Solido)
Si
OH
HO
O
Si
OH
OH
O
Si
O
OH
Si
O
OH
O
Si
OH
HO
OH
O
Paradifenolo
Ortodifenolo
O
O
Cicloesano
Etileacetato
O
Si
OH
Cromatografia di ripartizione
Fase mobile
Supporto solido
Fase stazionaria (liquida)
Un esempio di cromatografia di ripartizione (fase inversa)
Silice (solido)
Si
O
Si
O
Si
O
Si
O
Si
O
Si
Fase stazionaria
Catene C18 (liquido)
Aldeide C7
N
O
H
40%
20%
H
H
O
80%
60%
Fase mobile
Altre fasi stazionarie
Si
NC
Si
Si
Si
NC
NC
NC
Si
Si
Si
Si
N
N
N
N
Cianoalchil
Amminoalchil
Si
Si
Si
Si
Si
Fenilalchil
O2N
Si
Si
Si
O2N
O2N
O2N
Nitroalchil
Cromatografia di esclusione
Cromatografia di scambio ionico
-
+
-
+
-
++
++ +
+ + +
+ +
+
Gruppi scambiatori di ioni
H3C
OH
-
SO3
-
H
+
CH 3
N
CH 3
R
Gruppo trimetilammonio
Scambiatore di anioni
R
Gruppo solfonato
Scambiatore di cationi
Cromatografia di affinità
Perché eseguire un’analisi cromatografica?
Analisi qualitativa
Analisi quantitativa
Indicazioni per identificare una sostanza
Quantificazione della sostanza
Analisi qualitativa
tR
tR
In generale sostanze diverse hanno tempi di ritenzione diversi
Analisi Quantitativa
h
h
Linea di base
Linee di base corrette (da valle a valle)
S = Base * Altezza/2
Totale = 1 + 2+ 3+ 2+ 1
Integrazione
=9
Normalizzazione interna
A
B
C
ST = SA+SB+SC
Il rivelatore risponde allo stesso modo con i vari componenti
%A = SA/ST*100
%B = SB/ST*100
%C = Sc/ST*100
Ancora normalizzazione interna
A
B
C
Il rivelatore non risponde allo stesso modo con i vari componenti
SA*fA/CA = SBfB/CB = SC*fC/CC
fA = 1
fB = SA/CA*CB/SB
S’A = SA * fA
fC = SA/CA*Cc/Sc
S’B = SB * fB
S’C = SC * fC
Stot = S’A + S’B + S’C
CA= SA/STot
CB= SB/STot
CC= Sc/STot
Taratura diretta
A
B
POSSIBILITÀ DI DETERMINARE LA CONCENTRAZIONE DEL SOLO
COMPONENTE CHE INTERESSA
SS/CS = SC/CC
CC=SC*CS/SS
S = standard
C = campione
Standardizzazione esterna
S
Risposta
Peso
PA = peso del componente ricavato dal grafico
%A=PA/PC*100
PC = peso del campione iniettato
Standardizzazione interna
SA/SI.S.
PA/PI.S.
QA = PA/PI.S.*QI.S.
I st.
II st. III st.
Campione
incognito
Standard interno
Sostanza da dosare
Campione incognito
2 ml
2.000.000
= 0,5
4.000.000
1ml
1.000.000
= 0,5
2.000.000
Metodo dell’aggiunte multiple
S
Px
Paggiunto
CX=PX/VX