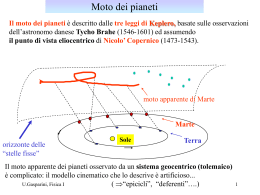
Equazioni differenziali omogenee e non omogenee :
Esempi di equazioni differenziali lineari “omogenee” (del secondo ordine):
d 2 x (t )
dt
2
d 2 x (t )
dt 2
2
 0
x (t )  0
 2
dx ( t )
2
 0
x (t )  0
dt
Equaz.differenziali lineari “non omogenee” ( “associate” alle precedenti):
d 2 x (t )
dt 2
d 2 x (t )
dt 2
2
 0
x (t )  f (t )
 2
dx ( t )
2
 0
x (t )  f (t )
dt
funzione incognita
U.Gasparini, Fisica I
“termine noto”
(funzione nota del tempo)
1
Soluzione generale delle equazioni differenziali non omogenee :
Importante proprietà:
nota una “soluzione particolare” xp (t) dell’eq. non omogenea,
la sua soluzione generale è data da:
y(t) = x(t) + xp
(t)
soluzione generale
dell’ eq.omogenea associata
Infatti:
d 2 x p (t )
{
dt 2
d 2 x (t )
dt 2
2
 0
x p (t )  f (t )
2
 0
x (t )  0
d 2 x (t )
dt
2

d 2 x (t )  x p (t )
dt
2
U.Gasparini, Fisica I
2
 0
x (t ) 
d 2 x p (t )
    x (t )  x
2
0
dt
p
2
(t )

2
 0
x p (t )  f (t )
d 2 y (t )
dt
2
2
 0
y (t )  f (t )
2
Oscillatore armonico “forzato” :
Su di esso agisce una forza (aggiuntiva) nota F(t);
particolare interesse ha il caso:
F (t )  F0 sin t




ma  Fel  v  F (t )



  kxu x  v  F0 sin tu x
d 2 x (t )
dt
2
 2
Soluzione generale:
F0
dx ( t )
2
  0 x (t ) 
sin t
dt
m
dove si è definito: 02 
k

, 
m
2m
x ( t )  Ae 1t  Be  2 t  x p ( t )
soluzione generale
dell’eq.omogenea associata: moto smorzato xom (t) 
t 
soluzione particolare dell’eq.non omogenea:
soluzione “di regime”: x (t) xp (t)
t 
U.Gasparini, Fisica I
3
Soluzione “di regime”
Soluzione particolare dell’eq. per un moto armonico forzato da una forza
F (t )  F0 sin t
:
x p (t )  A( ) sin(t   ( ))
“pulsazione forzante”
ampiezza e sfasamento dipendenti da 
Imponendo che xp(t) sia soluzione dell’ equazione completa (non omogenea) :
d
2
x p (t )
dt 2
 2
dx p ( t )
dt
2
 0
x p (t ) 
F0
sin t
m
  2 A sin(t   )  2A cos(t   )   02 A sin(t   )
cost cos  sin t sin 

F0
sin t
m
sin t cos  cost sin 
U.Gasparini, Fisica I
4
Fase ( ) :
( 02   2 ) A[sin t cos   cos t sin  ] 
F0
2A[cos t cos   sin t sin  ] 
sin t
m

[( 02   2 ) A cos   2A sin  ] sin t 

[( 02   2 ) A sin   2A cos ] cos t 

F0
sin t
m
F0
m
  2 ) A sin   2A cos  0
( 02   2 ) A cos  2A sin  
( 02
2
( 0
  2 ) tan   2  0
A[( 02   2 )  2 tan  ] 
U.Gasparini, Fisica I
tan  
F0
F0

m cos
m
2
 02   2
1  tan 2 
5
Ampiezza A() :

4 2 2
2
2
A ( 0   ) 
 02   2


A[( 02   2 ) 2  4
A( ) 
2
2] 

F0


m


F0
m
1
4
( 02
2
  2 )2
2
( 02   2 ) 2  4
2
2
F0 / m
( 02   2 ) 2  4
  2
 ( )  arctan  2
2




 0
2
2




A( ),  ( ) : ampiezza e fase del moto “a regime” xP (t)
non dipendono dalle condizioni iniziali,
che determinano le costanti A , B della
“parte transitoria “ del moto :
xom (t) = A0 et + B0 ebt
U.Gasparini, Fisica I
6
Moto di un oscillatore forzato
da una forza : F (t )  F0 sin t
x(t )  xom (t )  x p (t )
xom ( t )
x p (t )
x (t ) 
xom (t )  x p (t )
U.Gasparini, Fisica I
7
L’ampiezza dell’oscillazione forzata dipende dalla frequenza forzante :
A( ) 
 0  300rad / s
F0 / m
2
( 0
  2 ) 2  4
2
2
“curva di risonanza”

1
 0
T0
2
 100 Hz
0 
  30s 1
  0 / 10
  6s 1
  0 / 50
M 
 02 
100.
2
200.
300.
400.
 (rad/s)
dA( )
 0
d
  M
Massimo della ampiezza :
2
2( 0
2
M )( 2 M )  8
U.Gasparini, Fisica I
2
M  0
2
M 

2
0
 2
2
8
Sfasamento:
Lo sfasamento del moto rispetto alla forza  ( )
dipende dalla frequenza forzante:
  2
 arctan  2
2

0  




0.


2

Alla risonanza il moto è “in quadratura” (rispetto alla forza F(t)):
U.Gasparini, Fisica I
 ( 0 )
 / 2
9

Ampiezza massima:
La risonanza si ha solo per < :
AM
  0
  0
A M  A(

M
F0 / m
) 
2
2
( 0
2
)
 4
M
2
2
M
F0 / m
4
4
 4
2
2
( 0
 2
AM 
U.Gasparini, Fisica I
2
)
F0
2m
 02  
2
10
Potenza fornita all’oscillatore
Potenza istantanea fornita all’oscillatore dalla forza F (t )  F0 sin t :
P(t )  v (t ) F (t )  A( ) cos(t   ( )) F0 sin t
cost cos  sin t sin 
 A( )F0 [cost sin t cos  sin 2
t sin  ]
1
sin 2t
2
1
 A( )F0 [
sin 2t cos  sin 2 t sin  ]
2
valor medio nullo
su un periodo
Potenza media su un periodo:
1
< P 
T
T

< P  
0
1
P ( t ) dt   F0 A( ) sin( ( ))
T
T
 sin
2
tdt 
0
1
F0 A( ) sin( ( ))
2
tan 
1  tan 2 

2
2 / ( 2   0
)
1  4
2
 2 / ( 2   02 ) 2


1
2
2
2 2
( 2   0
) 4

11
2
2
Potenza trasferita all’oscillatore:

< P 
F0 A( ) 2
2 2
( 2   0
)  4
2
2
 mA 2 ( ) 2
A( ) 
< P  m 2 A2 ( )

F0 / m
2 2
( 2   0
)  4
2
2
La potenza media massima trasferita si ha per
   0 e vale:
< P  MAX  m
2
0
F02
A (0 ) 
4m
2
A( 0 ) 
F0 / m
4
2
 02

F0
2 0 m
( l’ampiezza massima si ha invece per
  M 
U.Gasparini, Fisica I
 02  2
2
)
12