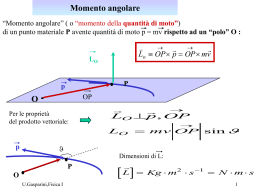
“Lavoro” compiuto da una forza :
v(t3)
v(t2 )
ds
v(t 1)
B

m
F


dW  F  ds  Fds cos
A
lavoro infinitesimo :
B
lavoro da A a B :
WAB 
 dW
A
B




F  ds
A
unità di misura del lavoro (S.I.): [W]= N m Joule
Esempio:
B
lavoro della forza d’attrito dinamico:
W
attr
AB


 attr

F
 ds 


  m D mgux  Ds AB   m D mgDs AB
A

ux
Fattr =-mDmgux
A
U.Gasparini, Fisica I
v
Ds
B
x
1
Lavoro della forza peso:
z
zA
A
( I)
zB
ds
mg
(III)
(II)
ds
dz
 ds cos
B

mg


mg  ds  mgds cos  mgdz
B
WAB 



mg  ds   mg
A
B
 dz  mg ( z
A
 zB )
A
lavoro indipendente dal cammino percorso:
W(I)AB = W(II)AB = W(III)AB

la forza peso é un esempio di “forza conservativa”
U.Gasparini, Fisica I
2
Potenza istantanea:
lavoro compiuto per unità di tempo ad un dato istante:
P( t ) 
Unità di misura (S.I.) :
dW ( t )
dt
[P] = [W] / [t] = J / s W (“Watt”)
Se F è una forza applicata ad un punto materiale in moto con velocità v,
la potenza sviluppata dalla forza F è:




F ( t )  ds
P(t ) 
 F (t )  v (t )
dt
 P 
Potenza media:
W
Dt
lavoro compiuto in un dato tempo diviso il tempo impiegato.
Altre unità di misura di uso pratico:
Lavoro:
KWh  1KW  3600s  3.6  106 J
Potenza:
U.Gasparini, Fisica I
h. p.  745.7W
“chilowattora”
“cavallo vapore”
3
Campo vettoriale
E’ definito quando in ogni punto di una data regione dello spazio è definito un vettore,
ossia siano date tre funzioni dei punti dello spazio, in generale indipendenti,
che rappresentino le componenti (ad es. cartesiane) di un vettore.
Esempio:
campo vettoriale delle velocità delle particelle di un fluido in moto.
“Campo di forza”:
campo vettoriale che rappresenta, in ogni punto dello spazio in cui è definito,
la forza cui un punto materiale è soggetto quando si trova in quel punto
 introduzione del concetto di “azione a distanza”
In situazioni “statiche” ( sorgenti della forza indipendenti dal tempo) è un utile
strumento matematico; in situazioni dinamiche (sorgenti della forza in moto), è
indispensabile per la decrizione descrive.
U.Gasparini, Fisica I
4
Campo di forza conservativo
Campo di forza per il quale il lavoro lungo qualsiasi percorso chiuso sia nullo :

 

F (r )  ds  0
per qualsiasi curva chiusa 
ds
r
F( r )

o, equivalentemente:
B

A


F  ds 
B

A
1
A
U.Gasparini, Fisica I


F  ds
per qualsiasi coppia di punti A,B
e per qualsiasi percorso
1 ,2 che li congiunge
2
1
B
2
5
Energia cinetica
“Energia cinetica” di un punto materiale di massa m e velocità v :
Ek 
 E k   kgm2 s 2
( dimensioni:
1 2
mv
2
 mkgms 2  mN  J
)
Per un punto materiale in moto da un punto A ad punto B sotto l’azione
di una forza risultante F vale il teorema dell’energia cinetica :
B
DE k 
E kB

E kA
 WA  B 

 
F  ds
A
vA
A
m
E kA
vB
B
1

mv A 2
2
U.Gasparini, Fisica I
F
E kB 
1
mv B 2
2
6
Teorema dell’ energia cinetica
aT
B
ds
a
s(t)
aN

A
B
WA B 



F  ds 
A



dv (t )
dv (t ) 
v2 


uT 
uN
dt
dt



m
dv (t )
ds 
dt



ma  ds 
A

dv ( s)
mv
ds 
ds
U.Gasparini, Fisica I
B
m
B

A
dv( s(t ))
ds 
dt
B
 ma
T ds
dv ( t )
dt

A

m
dv ( s) ds(t )
ds
ds
dt
1
1
2
mvdv  mv B  mv 2A  E kB  E kA
2
2
7
Esempio: moto lungo un piano inclinato privo d’attrito
la reazione vincolare non compie lavoro
F
a
0
a 
mg
d 2 x (t )
dt

l
condizioni iniziali:
dalla legge di Newton:
2
 g sin 
x
x0  0, v0  0
Integrando l’equazione
del moto:
v (t )  g sin t
x (t ) 
1
g sin t 2 , x (t f )    t f 
2
v f  v (t f )  g sin t f 
2
g sin 
2g sin 
Utilizzando il teorema dell’energia cinetica, si giunge allo stesso risultato:
=0
f
DE k  E k
U.Gasparini, Fisica I
 E ki 
1
mv 2
f  Wi  f
2
vf 
2g sin 
 mg sin 
lavoro della forza peso
8
Energia potenziale
Per un campo di forza conservativo, si definisce “energia potenziale” quella
funzione dei punti dello spazio tale che la sua differenza tra due qualsiasi punti
A, B sia uguale a meno il lavoro compiuto dalla forza del campo per andare da
A a B (lungo un qualsiasi percorso):
DE pAB



( r )  E p ( rB )  E p ( rA )  WA B  
B

 

F ( r )  ds
A



E p ( rB )  E p ( rA )  WA B  E p ( rA ) 
ossia:
B

 

F ( r )  ds
A
E pB  E p ( x B , y B , z B )  E p ( x A , y A , z A ) 
B
E pA  E p ( x A , y A , z A )

uz

ux
rA
o

x
A
A
rB

uy
 [F
B
( x , y , z ) dx  Fy ( x , y , z ) dy
 Fz ( x , y , z )dz]



F
(
x
,
y
,
z
)
u

F
(
x
,
y
,
z
)
u
x
x
y
y
F( r )

 Fz ( x , y , z ) u z
l’energia potenziale è definita a meno di una costante arbitraria
( al valore ad essa convenzionalmente assegnato in un punto arbitrario)
U.Gasparini, Fisica I
9
Energia meccanica
E’ la somma dell’ energia cinetica e dell’ energia potenziale :
EM


(r , v )  E k  E p (r )
Principio di conservazione dell’energia meccanica :
nel moto di un corpo in un campo di forze conservativo,
l’energia meccanica è costante :
 per due punti qualsiasi
A,B della traiettoria :
B
E kA  E pA  E kB  E p
Infatti:
B
E kB  E kA  WA B   DE p  E pA  E p
teorema
dell’ energia cinetica
U.Gasparini, Fisica I
definizione di
energia potenziale
10
Esempio: energia potenziale della forza peso:
B
z
DU  U B  U
A
 
A
zA



mg  ds 
A
zB
 mgdz  mg ( z
B
 zA)
A
U B  U A  mg ( z B  z A )
B
mg
B
O
Il punto A può essere scelto nell’origine: A  O
 zA  0
 U B  U O  mgz B
[ ovvero, considerando il percorso OA:
U A  U O  mg ( z A  zO )
 U B  U O  mg( z A  zO )  mg( z B  z A )  U O  mg( z B  zO )]
Posto :
U O  0.
 U B  U ( z B )  mgz B
ossia, per il generico punto P di coordinata z :
U ( z)  mgz
U.Gasparini, Fisica I
11
Esempio: conservazione dell’energia meccanica nel
moto di un corpo sotto l’azione della forza peso.
z
v0
h
mg
x
E iM 
1
1
f
2
mv0
 mgh  E M

mv 2
2
2
v
2
v 2  v0
 2 gh
[ dall’equazione del moto si giunge allo stesso risultato:
v x (t )  v0 x
v z ( t )  v 0 z  gt
z ( t )  h  v0 z t 
z (t
vz
f
 v0 z  gt
f
 v0 f 
)  0tf  

 v0 z 
 v0 z  

2
2
v2
 v xf
 v zf
f
U.Gasparini, Fisica I
f
1
gt 2
2
2
  
v0
z  2hg 

2
 / g
v0
f  2hg 

2
v0
z  2hg
2
2
2
 v0
x  v 0 z  2 gh  v 0  2 gh
12
]
Lavoro ed energia potenziale di una “forza elastica”


F ( x)   kxux
Forza elastica:
“costante elastica”: [k] = N / m
(il comportamento “elastico” dei materiali, cioè per deformazioni riproducibili
che non inducono modificazioni irreversibili della struttura, è descritto da una
legge di questo tipo, detta “legge di Hooke”)


F ( x)  kxux
0.
Lavoro:
2
W12 



F ( x )  ds  
1
2

1

ux
x
1
kxdx  
kx 2
2
x2
x1
1
2

k ( x12  x2
)
2
Energia potenziale:
DE p  E p ( x2 )  E p ( x1 )  W12 

E p ( x )  E p ( x1 ) 
Scelto x 10. e posto
U.Gasparini, Fisica I
1
k ( x22  x12 )
2
1
k ( x 2  x12 )
2
E p ( x  0.)  0.

E p ( x) 
1
kx 2
2 13
Bilancio energetico
In presenza di forze sia conservative che non conservative
( o “dissipative”) , vale l’equazione del “bilancio energetico”:


DE M (r , v)  D( E k  E p (r ))  WNC
energia potenziale
associata alle forze
conservative presenti
Infatti:
lavoro compiuto
dalle forze non conservative
E kf  E ki  W tot  WCons.  WNC   ( E pf  E ip )  WNC

E kf  E pf  ( E ki  E ip )  WNC
Esempio: moto lungo un piano scabro
z
E iM 
Fattr
zi
0
mg
l
U.Gasparini, Fisica I
1
mvi2  mgzi
2
1
f
EM

mv 2
f
2
1
1

mv 2f   mvi2  mgzi  
2

2
 WNC   Fatt  
  m D mg cos 
1
1
mv 2

mvi2  mgzi 
f
2
2
m D mg cos
Gradiente di una funzione scalare
La relazione che definisce l’energia potenziale di un campo di forza conservativo:

DE pAB ( r )  
B

 

F ( r )  ds
A
può essere invertita, introducendo il concetto di “gradiente” di una funzione scalare:
data una funzione scalare V ( r ) = V(x,y,z) , si definisce il “gradiente di V”
il vettore , indicato con V, tale che per qualsiasi spostamento
infinitesimo dr risulti:





V  dr  dV  V (r  dr )  V (r )

V cos dr  dV

V (r )
V
P
U.Gasparini, Fisica I
dr
P’
Il prodotto scalare del vettore
gradiente di V nel punto r con il vettore dr è
uguale alla variazione infinitesima della
funzione V( r ) tra il punto r e il punto r+dr


V (r  dr )

dV
V cos 
dr
15
Gradiente di una funzione scalare (II)
La “derivata direzionale”(limite della variazione per unità di spostamento
della funzione V( r ) lungo la direzione Dr ):





dV
V ( r  Dr )  V ( r )

 lim
 V cos   V

dr
Dr
Dr  0
é massima (cos = 1 ) quando dr é diretto lungo la direzione del gradiente di V
il gradiente di V é un vettore diretto lungo la direzione di massima
variazione (per unità di spostamento) della funzione V( r );
il suo modulo é uguale al valore della derivata
direzionale di V( r ) lungo tale direzione;
il verso è quello in direzione dei valori crescenti di V
Superfici
a egual valori di V
dV  V2  V1 
V
dr1
dr2
U.Gasparini, Fisica I
V( r ) = V2
dV
dV
dr1 
dr2
dr1
dr2
dV
dV

dr1
dr2
V( r ) = V1
16
Esempio: gradiente di una funzione scalare V(x,y)
In uno spazio bidimensionale (per es.: V(x,y)= h altezza del suolo s.l.m.)
V(x,y)
400
300
200
100
y
x
y
curve di egual livello
P1
V=100
V=200
V
V
V=300
V=400
P2
V
P3
x
Il gradiente di V in ogni punto P è diretto perpendicolarmente alle curve di egual livello
(ossia lungo la direione di massima pendenza del terreno)
U.Gasparini, Fisica I
17
Rappresentazione del gradiente in coordinate cartesiane
Per una funzione V( r ) = V(x,y,z) :



dV  V ( r  dr )  V ( r ) 
V ( x  dx , y  dy , z  dz )  V ( x , y , z ) 
V ( x , y , z )
V ( x , y , z )
V ( x , y , z )

dx 
dy 
dz
x
y
x
“derivate parziali”

V ( x  dx , y , z )  V ( x , y , z )
Dx 0
Dx
lim

Dalla definizione di gradiente: V  dr  dV  V (r  dr )  V (r)





V  dr  V
dx  V
dy  V dz  dV


 

V 

V 

V
U.Gasparini, Fisica I

x
x
y
z

y
V ( x , y , z )
x
V ( x , y , z )

y
V ( x , y , z )

z



z
rappresentazione del
vettore gradiente in coordinate
cartesiane ortogonali
18
Rappresentazione del gradiente in coordinate polari
Per una funzione V( r ) = V(r,,j) :
V ( r ,  , j )
V ( r ,  , j )
V ( r ,  , j )
dr 
d 
dj
r

j
dV 
lo spostamento dr ha componenti polari:




dr  drur  rdu  r sin djuj

ur
z
dr
P=( r,,j

j
x




V  dr  V


V

r
P’=( r+dr, +d, j+dj
d
dj
y
r sin

r
V

,
r
U.Gasparini, Fisica I

u
r

uj
dalla definzione di gradiente:


dr  V


V

1 V

,

r 



rd  V


V
j r sin dj  dV
j

1
V
r sin  j
19
Forza : gradiente dell’energia potenziale
 


dE p ( r )   F ( r )  ds
Dalla definizione di
energia potenziale:
E p
E p
E p
dx 
dy 
dz   ( Fx dx  Fy dy  Fz dz )
x
y
z
E p ( x , y , z )
x
E p ( x , y , z )
Fy ( x , y , z )  
y
Fx ( x , y , z )  
Fz ( x , y , z )  
E p ( x , y , z )
z
Esempio:
dall’energia potenziale della forza peso :
Fx ( x , y , z )  
Fy ( x , y , z )  

 

F (r )  E p (r )
E p
 0
x
E p
 0
y
E p ( x, y, z)  mgz  c
E p
Fz ( x , y , z )  
  mg

z
U.Gasparini, Fisica I

F  (0,0,mg )
20
Superficie equipotenziale
E p ( x , y , z) 


E p   F
luogo dei punti dello spazio aventi lo stesso
valore dell’ energia potenziale
costante
z
per uno spostamento ds lungo la superficie,
per definizione:
ds
y
dE p  0
x


dE p  E p  ds  0


Il vettore: E p   F


E p ds
è in ogni punto dello spazio perpendicolare alla superficie equipotenziale
passante per quel punto.
Esempio: superfici equipotenziali della forza peso
E p ( z)  mgz = costante
EP = - mg
z
y
x
U.Gasparini, Fisica I
mg
21