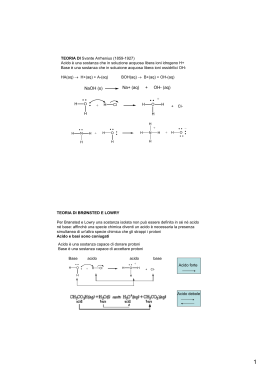
Definizione di acidi e basi secondo la teoria di BrönstedLowry
Un acido è una sostanza che cede ioni idrogeno (protoni) trasformandosi
nella sua base coniugata
AH ⇔ H+ + A −
acido
base coniugata
mentre una base è una sostanza che acquista protoni trasformandosi nel
suo acido coniugato
+
+
B + H ⇔ BH
base
acido coniugato
una base è una sostanza con almeno una coppia solitaria che cede un
elettrone al protone idrogeno per formare un legame covalente
Esempi
CH3COOH + H2O
NH3 + H2O (g)
CH3COO– + H3O+
NH4+ + OH–
Esercizio: Quali delle seguenti molecole possono essere basi di Bronsted?
a) H2O
b) CH4
c) PH3
d) BH4-
Metodo di risoluzione: disegnare le strutture di Lewis ed individuare
quale tra le strutture ha una coppia solitaria.
Soluzione: a) c)
L'autoionizzazione dell'acqua: se considero 2 molecole di acqua una si
comporta da acido e una da base
H2O + H2O =
acido 1
base 2
H3O+ + OH–
acido 2 base 1
Anche se in misura molto piccola, questa reazione tra molecole d’acqua,
detta di autoionizzazione, decorre veramente
[H3O+][OH–]
K = ————————
[H2O]2
K·[H2O]2 = Kw = [H3O+][OH–]
Kw : costante del prodotto ionico dell'acqua o prodotto ionico dell'acqua
a 25 °C:
Kw = [H3O+][OH–] = [OH–]2 = [H3O+]2 = 10–14
[OH–] = [H3O+] =
Soluzione neutra
Soluzione acida
Soluzione basica
10–14 = 10–7 M
[H3O+] = [OH–]
[H3O+] > [OH–]
[H3O+] < [OH–]
ACIDI E BASI FORTI E DEBOLI IN SOLUZIONE ACQUOSA
Se introduco un acido in acqua aumenta la concentrazone di H+ e
diminuisce quella di OH- ( Kw è una costante a temperatura
costante).
AH ⇔ H+ + A −
acido
base coniugata
[
H ]⋅ [A ]
=
+
Ka
−
[HA]
Costante di dissociazione
dell’acido
Indica quanto l’acido è dissociato all’equilibrio
Ka<<1
Ka>1
Ka>55
[H ]⋅ [A ] << [HA]
[H ]⋅ [A ] > [HA]
[H ]⋅ [A ] >> [HA]
+
−
+
+
−
Acido debole poco dissociato
Equilibrio spostato a sinistra
Acido forte dissociato
Equilibrio spostato a destra
−
Acido forte completamente dissociato
ACIDI E BASI FORTI E DEBOLI IN SOLUZIONE ACQUOSA
Se introduco una base in acqua diminuisce la concentrazone di H+
e aumenta quella di OH- ( Kw è una costante a temperatura
costante).
+
B + H 2O ⇔ BH + OH
base
acido coniugato
[
BH ]⋅ [OH ]
=
+
Kb
−
−
[B]
Costante di dissociazione della
base
Indica quanto la base è dissociata all’equilibrio
Kb<<1
Kb>1
[BH ]⋅ [OH ] << [B]
[BH ]⋅ [OH ] << [B]
[BH ]⋅ [OH ] << [B]
+
+
−
+
Kb>55
−
−
Base debole poco dissociata
Equilibrio spostato a sinistra
Base debole dissociato
Equilibrio spostato a destra
Base forte completamente dissociato
pH, pOH, pK
p(….) = –log(…)
pH = –log [H3O+]
il logaritmo della concentrazione molare degli ioni idrogeno presenti
in tale soluzione cambiato di segno
pOH = –log [OH–]
pK = –log K
Per soluzioni acquose a 25°C
Kw = [H3O+][OH–] = 10–14
pKw=14
pH+pOH= 14
pH<7 soluzione acida ;
pH > 7 soluzione basica
pH =7 soluzione neutra
pH=14-pOH
Il pH di soluzioni di acidi forti, o di basi forti diluiti
HA + H2O
H3O+ + A–
[H3O+] = [HA] perché è completamente dissociato
pH = –log [H3O+]= –log [HA]= –log cA
per soluzioni di acidi forti monoprotici la concentrazione degli ioni
idrogeno è pari alla concentrazione molare dell’acido stesso
pOH, di una soluzione di BOH con concentrazione Cb
BOH
OH- + B+
[OH-] = [BOH]
pOH = –log [OH-]= –log [BOH]= –log cB
per soluzioni di basi forti monoidrossiliche la concentrazione degli ioni
idrossile è pari alla concentrazione molare della base stessa
B(OH)n
nOH- + B+
pOH = –log n[OH-]= –log ncB
Il pH di soluzioni di acidi forti, o di basi forti diluiti
Sono forti tutte le basi dei metalli del primo e del secondo gruppo
Esercizi sul calcolo del pH per acidi e basi forti
Calcolare il pH di una soluzione 1,71x10-4 M di HCl.
pH = − log10 ca
pH = − log10 (1,71 ⋅10 −4 ) = − log10 1.71 − log10 10 −4 = − log10 1,71 + 4 = 3.77
Esercizi sul calcolo del pH per acidi e basi forti
Calcolare il pH di una soluzione 2x10-3 M di HCl
Controllare sempre se l’acido è forte
Controllare sempre la concentrazione dell’acido
pH = − log10 ca
pH = − log10 (2 ⋅10 −3 ) = − log10 2 − log10 10 −3 = − log10 2 + 3 = 2.7
−3
log10 10 = −3 log10 10 = −3 ⋅1
Esercizi sul calcolo del pH per acidi e basi forti
Qual è la concentrazione di OH- in una soluzione con pH=5,14?
I metodo
pH+pOH=14
pOH=14-5.14=8,86
[
pOH = − log10 OH −
[OH ] = 10
−
II metodo
]
−8.86
pH = 5,14
[H ] = 10 = 10
[OH ]⋅ [H ] = 10
10
10
[OH ] = [H ] = [10 ] = 10
+
− pH
−
−
+
−5,14
−14
−14
−14
+
−5.14
−8,86
Esercizi sul calcolo del pH per acidi e basi forti
Se una soluzione ha pH 2,57, la concentrazione di OH- sarà ?
[OH ]
−
10 −14
= − 2,57 = 10 −11, 43 = 3,7 ⋅10 −12
10
Esercizi sul calcolo del pH per acidi e basi forti
Calcolare pH e pOH per 14 mg di NaOH disciolti in 250ml di soluzione.
Controllare sempre se la base è forte
Controllare sempre se la base è monoprotica
NaOH è una base forte completamente dissociata
Per poter porre
nNaOH
c NaOH
[OH ] = c
−
B
controllo che CB>10-6 mol/l
14 ⋅10 −3 ( g )
=
= 3,5 ⋅10 − 4 mol
39,98( g / mol )
nNaOH
3,5 ⋅10 −4 (mol )
−3
=
=
=
1
,
4
⋅
10
(mol / l )
−3
Vsoluzione
250 ⋅10 (l )
CB>10-6 mol/l
p (OH ) = − log10 cB
Esercizi sul calcolo del pH per acidi e basi forti
pOH = − log(1,4 ⋅10 −3 ) = − log 1,4 + 3 = 2,85
pH=14-pOH= 15-2,85=11,146
Esercizi sul calcolo del pH per acidi e basi forti
Calcolare il pH per una soluzione di Ba(OH)2 1x10-3 M
ATTENZIONE! LA BASE SI DISSOCIA DANDO 2 MOLI DI OH- PER
OGNI MOLE DI IDROSSIDO
[OH ] = 2 ⋅ c
−
B
= 2 ⋅ (1⋅10−3 M ) = 2 ⋅10−3 (mol / l )
pOH = − log10 2cB = − log10 (2 ⋅10 −3 ) = 2,7
pH=14-pOH=14-2,7=11,3
Esercizi sul calcolo del pH per acidi e basi forti
Calcolare il pH di una soluzione di HCl 1x10-8 M.
HCl si dissocia completamente:
[ ]
c A = H + = 1 ⋅10 −8 M
ma è molto diluito
Non posso trascurare il contributo
della dissociazione dell’acqua.
cA<10-6 (mol/l)
[H ] = [H ]
+
+
tot
[ ]
+
+
H
acido
H 2O
= 1 ⋅10 −8 + 1 ⋅10 −7 = 1,1⋅10 −7 M
pH = − log10 1,1⋅10 −7 = 6,96
Se non avessi considerato l’acqua:
pH = − log10 1 ⋅10 −8 = +8!!!!
Assurdo!!!
Il pH di soluzioni di acidi deboli o di basi deboli
pH di una soluzione di HA
HA + H2O
cA = concentrazione molare iniziale dellacido
[A–][H3O+]
Ka = ———————
[HA]
H3O+ + A–
AH
H2O
A-
H3O+
Inizio
cA
-
0
0
Variazione
-x
-
+x
+x
Fine
c A- x
-
x
x
[A–][H3O+]
[x][x]
[H+][H+]
Ka = ——————— = ——————— = ——————
[HA]
[cA-x]
cA
[H ] =
+
K a ⋅ ca
Per le basi deboli
pH= - log
p0H= - log kBcB
pH=14-pOH
kAcA
ESERCIZIO
L’ammoniaca è una base debole avente Kb = 1.79.10-5; calcolare quale
concentrazione deve avere una soluzione di NH3 perché si abbia un pH di
10.824.
+
NH 3 + H 2O ⇔ NH 4 + OH −
[NH ][OH ] = 1.79 ⋅10
=
+
Kb
−
4
[NH 3 ]
−5
Ricordare sempre lo schema per l’equilibrio che permette di
ricavare la Ka o la Kb.
+
NH 3 + H 2O ⇔ NH 4 + OH −
inizio
Cb
0
0
∆
-x
+x
+x
Equilibrio
Cb-x
x
x
In questo caso dal pH possiamo ricavare [H+] e [OH-] quindi “x”.
H + = 10 − pH = 10 −10.824
−14
Kw
10
OH − = + = −10.824 = 6.67 ⋅10 − 4 M
10
H
[
NH ][OH ]
=
=
+
Kb
4
[NH 3 ]
Cb = 2.55 ⋅10 2
−
(
)
−4 2
x⋅x
6.67 ⋅10
−5
=
=
1
.
79
⋅
10
(Cb − x ) Cb − 6.67 ⋅10 −4
(
)
ESERCIZIO
Una soluzione acquosa di acido lattico 5.5.10-2 M ha un pH di 2.195.
Calcolare Ka.
Acido lattico: HA
H + = 10 − pH = 10 −2.195
pH = 2.195
Ricordo sempre lo schema di dissociazione per un acido
debole:
HA ⇔ A− + H +
inizio
Ca
0
0
D
-x
+x
+x
Equilibrio
Ca-x
x
x
[
H ][A ]
=
=
+
Ka
[HA]
−
(
H + = 10 −2.195
)
− 2.195 2
x⋅x
10
−4
=
=
8
.
38
⋅
10
(Ca − x ) 5.5 ⋅10−2 − 10−2.195
(
)
Se aggiungiamo 20 g di acido cloridrico e 20 g di idrossido di sodio e
aggiungiamo acqua fino a che il volume totale della soluzione risulta
essere 1 litro, la soluzione risultante sarà:
a) acida
b) basica
c) neutra
d) dipende dalla temperatura
Soluzione neutra
Soluzione acida
Soluzione basica
Ca=0,55M
[H3O+] = [OH–]
[H3O+] > [OH–]
[H3O+] < [OH–]
Cb=0,5M