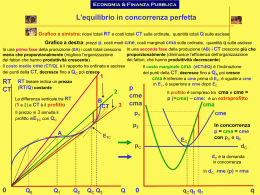
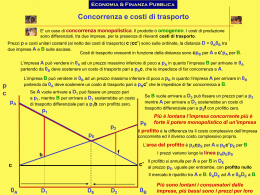
Massimizzazione del profitto
P = RT - CT
Massimizzazione del profitto
(a) impresa senza
potere di mercato
(price-taking: P è dato)
fig
CT = Costo totale di Breve periodo
CT
CT
600
500
400
300
200
100
0
0
10
20
30
40
50
60
quantità
RT ricavo totale con P dato
CT
RT
CT
600
RT
500
400
300
200
100
0
0
10
20
30
40
50
60
quantità
a,b punti di pareggio
CT
RT
CT
600
b
RT
500
400
300
a
200
100
0
0
10
20
30
40
50
60
quantità
Massimizzazione del profitto


Poiché il profitto è definito come
differenza tra ricavi totali e costi totali,
rendere massima questa differenza
consiste nel cercare il punto di massima
distanza tra le due funzioni RT e CT
Il punto così trovato ci indica la quantità
ottimale per l’impresa (P è dato).
CT
RT
600
500
Il punto di max distanza si
trova tracciando la tangente a
CT parallela a RT, ovvero:
angoli  uguali
CT
b
RT
400
300

a
200
100
0
0

10
20
30
40
50
60
quantità
CT
RT
600
La massima distanza corrisponde al
segmento a-b e la quantità ottima
è Q = 46
CT
RT
500
a
400
385
90
295
b
200
100
0
0
10
20
30
40
46 50
60
quantità
Massimizzazione del profitto
(b) impresa con curva di
domanda inclinata
negativamente
fig
Tabella dati
quantità
RT
CT
Profitto
0
0
6
-6
1
8
10
-2
2
14
12
2
3
18
14
4
4
20
18
2
5
20
25
-5
6
18
36
-18
7
14
56
-42
CT
24
RT, CT, T (€)
20
16
RT
12
Anche in questo caso dobbiamo
trovare il punto di massima
distanza che corrisponde
al punto in cui le due tang.
sono parallele
8
4
0
1
-4
-8
2
3
4
5
6
7
quantità
CT
24
RT, CT, T (€)
20
16
RT
12
8
4
0
1
2
3
4
5
6
-4
-8
T
7
quantità
CT
24
b
RT, CT, T (€)
20
16
RT
a
12
Punti di
pareggio
8
4
c
0
1
d
2
3
4
5
6
-4
-8
T
7
quantità
CT
24
22
20
d
RT, CT, T (€)
18
16
14
RT
e
12
Punto di max
profitto
10
8
6
f
4
2
0
-2
1
2
3
4
5
6
-4
-6
-8
T
7
quantità
Max profitto

La quantità che massimizza il profitto
dell’impresa è quella in corrispondenza di
RMg = CMG (ricavo marginale = costo
marginale)
24
DQ
RT, CT, T (€)
20
CT
a
DRT
16
b
12
DCT
RT
DQ
8
4
0
1
-4
-8
2
3
4
5
6
7
quantità
RMg = CMG
DRT
DCT
a=b
=
DQ
DQ
 RMg = CMG
Prof. Max. con le funzioni “medie”
RT  P  Q
CT  CMe  Q
  RT  CT
 P  Q  CMe  Q
 Q  ( P  CMe)
Massimizzazione del profitto
(a) Impresa Price-taking
Anziché tracciare le tangenti per trovare il punto
di massima distanza tra RT e CT illustriamo il
problema della massimizzazione del profitto
utilizzando le funzioni RMg e CMG
fig
Max profitto con P dato



Se l’impresa non ha potere di mercato:
RMe = P = RMg = costante
La funzione di domanda dell’impresa è
infinitamente elastica
Funzioni di costo dell’impresa
CMG
CME
CMG
50
CME
40
30
20
10
0
0
10
20
30
40
50
60
quantità
Costi e
Ricavi (€)
CMG
50
RMe = RMg
CME
40
38
30
20
10
0
0
10
20
30
40
50
60
quantità
Costi e
Ricavi (€)
CMG
50
RMe = RMg
40
38
CME
a
30
b
22
20
10
0
0
10
20
30
40
50
60
quantità
Max profitto



Punto a: incontro tra ricavo marginale e
costo marginale
Trovo sull’asse delle ascisse la quantità
che massimizza il profitto in
corrispondenza del punto a
Il segmento a-b misura il profitto
unitario
Costi e
Ricavi (€)
CMG
50
CME
40
38
30
a
Profitto tot. = €16 x 40 = €640
b
22
20
10
0
0
10
20
30
40
50
60
quantità
Massimizzazione del profitto
(b) curva di domanda
decrescente
fig
CMG
20
16
costi e ricavi (€)
12
8
4
0
1
-4
2
3
4
5
6
7
quantità
RMg
CMG
20
costi e ricavi (€)
16
12
8
Output che massimizza il profitto
e
4
0
1
-4
2
3
4
5
6
7
quantità
RMg
16
CMG
costi e ricavi (€)
12
CME
8
4
RMe
0
1
2
3
4
5
6
7
quantità
-4
RMg
16
CMG
costi e ricavi (€)
12
CME
8
a
6.00
4.50
b
4
RMe
0
1
2
3
4
5
6
7
quantità
-4
RMg
16
CMG
costi e ricavi (€)
12
CME
8
6.00
4.50
Profitto totale
4
RMe
0
1
2
3
4
5
6
7
quantità
-4
RMg
Massimizzazione del profitto
Minimizzazione delle
perdite
fig
CMG
costi e ricavi (€)
CME
RMe
O
RMg
quantità
CMG
costi e ricavi (€)
CME
RMe
O
Q
RMg
quantità
costi e ricavi (€)
CMG
CME
CME
RMe
RMe
O
Q
RMg
quantità
costi e ricavi (€)
CMG
CME
CME
Perdita
RMe
RMe
O
Q
RMg
quantità
Massimizzazione del profitto
Punto di fuga
nel breve periodo
fig
Punto di chiusura



I costi fissi sono già stati sostenuti
dall’impresa
L’impresa continua a produrre nel breve
periodo se riesce almeno a coprire i suoi
costi variabili
Se i ricavi non sono sufficienti allora
l’impresa chiude
costi e ricavi (€)
CME
CVME
RMe
O
quantità
costi e ricavi (€)
P=
CVME
CME
CVME
RMe
O
Q
quantità