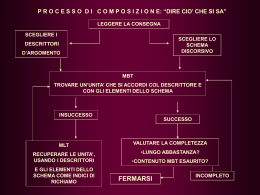
Analisi QSAR
di
Chiara Cappelletti, Davide Cittaro, Morena Spreafico, Marco Stefani
INTRODUZIONE
Dato un insieme di molecole congeneri vogliamo quantificare le differenze dell’attività biologica in
termini di differenze strutturali. A tale scopo abbiamo utilizzato il metodo di regressione lineare dei
Minimi Quadrati Ordinari formulando dei modelli QSAR.
Le differenze strutturali vengono rappresentate da un insieme di descrittori molecolari
appositamente scelti in modo da rendere il più completa possibile la rappresentazione delle
molecole. Con un numero di descrittori grande, probabilmente riusciremo ad ottenere una buona
descrizione della realtà in esame, ma il modello quasi sicuramente incorrerà nel fenomeno
dell’over-fitting, riducendo anche drasticamente la capacità predittiva per le nuove molecole. Un
buon modello mantiene generalmente il rapporto variabili-oggetti inferiore a 5, perciò diventa
indispensabile selezionare adeguatamente i descrittori in modo da ottenere un modello con una
buona capacità sia descrittiva che predittiva. Un ulteriore vincolo è dato dall’uso del metodo dei
minimi quadrati, che impone l’eliminazione delle variabili troppo correlate.
L’esplorazione esaustiva di tutte le possibili combinazioni di un insieme realistico (varie decine o
centinaia) di descrittori richiederebbe un tempo di calcolo troppo elevato; di fatto, ciò impedisce di
utilizzare degli algoritmi deterministici in grado di garantire la soluzione ottimale, e quindi
s’impone l’utilizzo di metodi approssimati. La nostra scelta ricade sugli algoritmi genetici che
permettono di esplorare in tempi ragionevoli lo spazio delle soluzioni.
Ottenuto il modello, un passo molto importante consiste nella validazione del modello stesso, cioè
la verifica della sua capacità predittiva nei confronti di molecole che non sono state utilizzate per la
costruzione del modello. Se il modello è robusto, il passo successivo consiste nell’interpretazione
del ruolo dei descrittori scelti.
ALGORITMI GENETICI PER LA SELEZIONE DELLE VARIABILI
Gli algoritmi genetici, proposti da Holland nel 1975, sono una strategia di ottimizzazione che si
ispira alla genetica delle popolazioni. Il processo di ricerca di una soluzione avviene tramite un
particolare bilanciamento tra l’esigenza di esplorare nuove regioni nello spazio delle soluzioni, e
quella di sfruttare con una ricerca locale le informazioni a disposizione.
La descrizione dei valori che ogni variabile può assumere avviene mediante un codice binario, ove
ciascun termine binario costituisce un bit, cioè un numero uguale a 0 o 1. Il linguaggio degli
algoritmi genetici ha un lessico appropriato in analogia con la genetica delle popolazioni:
o Gene: ciascuna codifica binaria di un numero (una variabile, un parametro numerico)
o Individuo o Cromosoma: l’insieme di più geni, cioè la concatenazione di più bits, ed è
associato ad una particolare soluzione
o Popolazione: l’insieme di individui o cromosomi
o Riproduzione, Cross-over, Mutazione: rappresentano gli operatori genetici che regolano
il processo di ricerca della soluzione ottima
Gli algoritmi genetici sono organizzati in tre fasi:
1. Fase iniziale: viene effettuata una codifica delle variabili mediante il codice
binario. Ciascuna condizione viene rappresentata da una stringa di 0 o di 1. Nella
selezione delle variabili che ottimizzano un modello di regressione, lo 0 indica
l’assenza della variabile nel modello mentre l’1 indica la presenza. Viene estratto
un certo numero di cromosomi a caso e per ciascuno di essi viene calcolata la
risposta corrispondente; i migliori entrano a far parte della popolazione iniziale.
2. Fase evolutiva: è costituita da una fase di generazione di cromosomi che
derivano dall’accoppiamento dei cromosomi presenti nella popolazione e calcolo
delle risposte corrispondenti, e da una fase di mutazione dove ciascun
cromosoma può casualmente subire delle mutazioni. In questo caso, viene
calcolata la corrispondente risposta. Se le risposte calcolate sono migliori della
risposta corrispondente all’ultimo cromosoma della popolazione (il peggiore
della popolazione esistente), i cromosomi corrispondenti entrano a far parte della
popolazione, nella posizione che loro compete in base alla qualità della risposta.
In caso contrario, i cromosomi vengono scartati. Esaminando più nel dettaglio,
durante la riproduzione sono estratti dei cromosomi destinati
all’accoppiamento, con probabilità proporzionale alla qualità del cromosoma.
Durante il cross-over vengono generati i cromosomi derivanti
dall’accoppiamento, scambiando i geni dei cromosomi genitori con una
probabilità prefissata (cross-over probability). Durante la mutazione alcuni geni
cambiano il loro valore da 0 a 1 e viceversa, secondo una determinata probabilità
(mutation probability). La fase evolutiva procede fino a che non si raggiunge
una condizione che pone termine alla procedura.
3. Fase finale: la procedura viene fermata in base a criteri prestabiliti, quali, ad
esempio, il raggiungimento di un numero massimo di iterazioni o quando la
popolazione non si rinnova per un certo numero di iterazioni.
Al termine della procedura si ottiene la selezione delle variabili migliori tra quelle che l’algoritmo
ha considerato; se tutto lo spazio delle soluzioni possibili è stato indagato, quella proposta è la
soluzione ottima.
DESCRIZIONE DEL PROBLEMA
Le molecole utilizzate per lo studio sono 14 isomeri delle PCDD (Poli-Cloro-dibenzo-diossina); è
importante sottolineare che le molecole analizzate sono strettamente congeneri e differiscono
solamente nel numero e nella posizione degli atomi di Cloro, pertanto rappresentano un set molto
omogeneo di composti per il quale ci si può aspettare una buona correlazione tra le strutture e la
attività biologica.
La risposta biologica per la quale viene costruito un modello di regressione è l’affinità di binding.
Al fine di calcolare i descrittori molecolari le 14 diossine sono state disegnate con il programma
MOE (Molecular Operating Environment) e successivamente sono state minimizzate attraverso i
metodi della meccanica molecolare. In particolare è stato utilizzato il campo di forza MMFF94
adatto a descrivere le proprietà di piccole molecole organiche.
I DESCRITTORI MOLECOLARI
La conformazione spaziale delle 14 molecole minimizzate è il punto di partenza per il calcolo
dell’insieme dei descrittori molecolari, effettuato con DRAGON.
Il linguaggio con cui descriviamo la realtà non coincide con la realtà stessa: per questo motivo le
parole che utilizziamo per esprimerci svolgono un ruolo importantissimo nella rappresentazione
della realtà. Nella costruzione di modelli QSAR i descrittori molecolari svolgono lo stesso compito
delle parole in un discorso: la qualità del modello finale, che ha lo scopo di rappresentare una parte
di realtà, nella fattispecie l’attività biologica dei composti analizzati, dipende strettamente dai
descrittori utilizzati. Essi sono il modo attraverso il quale l’informazione chimica è trasformata e
codificata. Ognuno di essi è un numero che descrive un aspetto strutturale della molecola: più un
descrittore sarà in grado di spiegare bene quell’aspetto, ovvero più il linguaggio è accurato e chiaro,
più il modello sarà buono.Per questo motivo la scelta dei descrittori riveste un ruolo fondamentale
nella formulazione di un modello.
Le classi di descrittori utilizzate in questo lavoro sono:
COSTITUZIONALI
Sono descrittori molto semplici, indipendenti dalla connettività e dalla conformazione. Indicano
il numero di alcuni atomi, o di legami, o la somma di alcune proprietà (volumi, elettronegatività,
polarizzabilità, etc.). Sono facili da ricavare ma la descrizione che danno della molecola è
piuttosto generica. Tuttavia, ciò non vuol dire che apportino un’informazione poco importante,
sono infatti descrittori molto semplici che si ritrovano spesso nei modelli calcolati.
TOPOLOGICI
Largamente utilizzati negli studi QSAR, sono descrittori 2D che derivano dal grafo molecolare
(solitamente tolti gli atomi di idrogeno) e dalle matrici di connettività. Sono prevalentemente
fondati sui concetti di entropia e di contenuto di informazione ed hanno la proprietà di essere
invarianti al grafo molecolare, cioè il loro valore è indipendente da come vengono numerati i
vertici del grafo. Sono semplici da calcolare ma i loro limiti più evidenti sono legati alla totale
mancanza di informazione riguardo alla geometria 3D e agli aspetti conformazionali, e alla non
sempre chiara interpretabilità chimica. A dispetto di ciò, si dimostrano spesso estremamente
efficaci per il loro alto potere modellante.
WHIM
Il calcolo di questi descrittori prevede la centratura della molecola nel centro delle coordinate e,
mediante l’analisi delle componenti principali, la determinazione degli assi principali. La
rappresentazione della molecola avviene mediante una proiezione degli atomi sui tre assi
principali e sul calcolo di alcuni parametri statistici (gli indici WHIM) per ciascuno di questi
assi, senza applicare schemi di pesatura oppure pesando attraverso le masse atomiche, i volumi
di Van der Waals, l’elettronegatività atomica di Mulliken, la polarizzabilità atomica o gli indici
elettrotopologici di Kier. Si ottengono così dei descrittori WHIM direzionali, che, per ogni
schema di pesatura, possono poi dar luogo anche ad indici globali, cioè non direzionali.
GETAWAY
Sono dei descrittori basati su una matrice d’influenza, chiamata Molecular Influence Matrix,
simile alla matrice dei Leverages solitamente usata nella regressione. Un primo set di
descrittori, chiamato H-GETAWAY, viene ottenuto utilizzando solo le informazioni provenienti
dalla Molecular Influence Matrix, mentre un secondo set, chiamato R-GETAWAY, combina
questa informazione con le distanze interatomiche nella molecola.
Le tre tipologie di descrittori sono state trattate separatamente considerando per ciascun insieme i
descrittori con una correlazione pairwise inferiore al 95%. Sono state ottenute rispettivamente 39,
11 e 22 variabili.
I PARAMETRI DI PERFORMANCE
Per ciascuno dei tre insiemi di descrittori abbiamo utilizzato gli algoritmi genetici per selezionare la
migliore combinazione di descrittori. Ogni modello è identificato da un cromosoma di lunghezza
pari al numero di descrittori per ogni insieme; il numero di descrittori selezionati in ciascun
cromosoma può variare tra 3 e 5. La popolazione è costituita da 100 individui e sono state effettuate
10000 iterazioni per ogni insieme di descrittori. La bontà dei modelli è valutata mediante un
parametro di fitting, il coefficiente di determinazione R2, e due parametri di validazione, R2cv e
R2LOO.
Il coefficiente di determinazione R² viene definito come:
( yi − yˆ i ) 2
RSS
∑
R = 1−
= 1−
TSS
∑ ( yi − y i ) 2
2
Questo valore, moltiplicato per 100, rappresenta la varianza percentuale spiegata dal modello in
fitting. La radice quadrata del parametro precedente è una quantità nota come coefficiente di
correlazione multipla, R, e rappresenta la correlazione tra la risposta sperimentale e i predittori.
Oltre a questi parametri, che misurano il fitting, ve ne sono altri che misurano la capacità predittiva
del modello.
Il parametro definito PRESS (Predictive Error Sum of Squares) è formalmente analogo a RSS, con
la differenza che al posto delle risposte calcolate vengono utilizzate le risposte predette.
PRESS =
∑ (y
i
i
− yˆ i / i ) 2
Analogamente al parametro R², sostituendo RSS con PRESS, viene definita la varianza spiegata dal
modello in predizione, ovvero:
Q2 = R2cv = 1-
PRESS
TSS
Diversamente da R2, questo parametro presenta un massimo per la complessità ottimale del modello
e ridiscende ogni volta che aggiungiamo al modello variabili non predittive. Inoltre Q2 viene
esplicitamente valutato rispetto al potere predittivo e non al livello di fitting del modello. E’ perciò
un parametro molto importante, soprattutto nel caso in cui il modello presuppone un suo utilizzo per
applicazioni successive su dati la cui risposta non è ancora nota.
La validazione è stata fatta secondo due diverse tecniche: attraverso il metodo Leave One Out,
sintetizzata dal parametro R2LOO, e attraverso il metodo Leave Many Out, descritta da R2cv.
Entrambe sono tecniche di cross validation; con questo termine si indica una validazione incrociata,
in cui un oggetto o un gruppo di oggetti viene utilizzato per la predizione una sola volta.
METODO LEAVE ONE OUT
Secondo questo metodo, dati n oggetti, si calcolano n modelli in ciascuno dei quali viene escluso un
oggetto alla volta: ciascun modello viene calcolato con gli n-1 oggetti restanti e viene utilizzato per
predire la risposta, che può essere di tipo qualitativo in un modello di classificazione o quantitativo
in un modello di regressione. Lo scarto tra la risposta predetta e quella sperimentale viene
accumulato per tutti gli oggetti che a turno vengono esclusi dal modello. Solitamente il modello
finale viene costruito considerando comunque tutti gli oggetti, in modo da sfruttare tutta
l’informazione disponibile. Questo metodo è l’unico che consente un confronto univoco tra modelli
ottenuti con metodi diversi, ed è quello che comporta la minima perturbazione in quanto viene
escluso un solo oggetto per volta, e per questo motivo talvolta fornisce risultati troppo ottimistici.
METODO LEAVE MANY OUT
E’ una generalizzazione del metodo precedente. Infatti i dati vengono suddivisi in G gruppi di
cancellazione in modo tale che k oggetti pari a n/G vengono assegnati all’insieme di valutazione e
quindi sono esclusi dal training set: il modello, stimato da un training set costituito da n-k oggetti,
viene utilizzato per predire la risposta dei k esclusi. I k oggetti vengono esclusi una volta soltanto;
una volta esclusi, vengono successivamente reinseriti nel modello e ne vengono esclusi altri k.
Rispetto al metodo precedente, questo è più perturbativo, e valuta in modo più severo la predittività,
ma i risultati ottenuti dipendono dalla ripartizione degli oggetti all’interno dei gruppi di
cancellazione.
La funzione obiettivo che guida la selezione delle variabili negli Algoritmi Genetici è il parametro
R2LOO e utilizza il metodo di regressione lineare dei Minimi Quadrati Ordinari.
RISULTATI
Riportiamo il miglior modello a 3, 4 e 5 variabili per ciascun insieme di descrittori. I modelli scelti
sono quelli che si comportano meglio per i tre parametri.
Costituzionali e Topologici
Getaway
WHIM
R2
0.994
0.943
0.978
0.921
0.952
0.924
0.638
0.635
R2LOO
0.938
0.894
0.93
0.858
0.912
0.125
0.173
0.335
R2cv
0.984
0.88
0.891
0.845
0.372
-0.921
0.122
0.288
N
5
4
5
4
3
5
4
3
Tabella 1 – Performance dei migliori modelli calcolati
Il fatto che nel gruppo Costituzionali e Topologici non vengano selezionati modelli a tre variabili ci
fa supporre che tre sole variabili non siano sufficienti a raggiungere la qualità dei modelli a 4 e 5
variabili.
I descrittori WHIM hanno una performance decisamente peggiore rispetto agli altri due insiemi. Il
valore negativo di R2cv per il modello a 5 variabili significa che i residui del modello sono tanto
superiori ai residui calcolati sul valor medio da far preferire il modello Zero, che seglie sempre il
valore medio. Il suo alto valore di fitting non è sufficiente a renderlo un buon modello per la
pessima capacità predittiva.
I modelli con basso numero di variabili sono preferibili perchè più semplici e più facilmente
interpretabili, e per la consuetudine di mantenere il rapporto oggetti/variabili superiore a 5, i modelli
a 3 variabili sarebbero stati preferibili. Nel nostro caso però il modello a 3 variabili ha un R2cv così
basso da escluderne la scelta. I descrittori Costituzionali e Topologici si comportano
complessivamente meglio e quindi saranno analizzati più nel dettaglio.
ID
1
2
3
4
5
6
7
8
R2
0.994
0.983
0.986
0.943
0.943
0.952
0.928
0.92
R2LOO
0.938
0.844
0.905
0.893
0.894
0.823
0.861
0.812
R2cv N
0.984 5
0.95 5
0.933 5
0.888 5
0.88 4
0.821 4
0.794 4
0.089 4
1
1
1
3
3
4
3
1
3
3
3
11
11
17
11
20
Variabili
20
20
15
20
25
25
20
25
23
21
20
25
36
29
25
29
37
37
37
36
Tabella 2 – Modelli per i descrittori Costituzionali e Topologici
Osserviamo che negli otto modelli selezionati solo 1/3 dei descrittori totali è rappresentato. Il fatto
che pochi descrittori ricorrano frequentemente è indice di robustezza dei modelli. Secondo noi il
miglior modello è il numero 5, perché ha 4 variabili e perché tra i modelli a 4 variabili ha la
migliore performance, sia in fitting che in predizione.
L’equazione del modello è la seguente:
y = 36.324 - 0.009 * MSD -328.954 * TIE -10.725 * Xindex + 2.351 * PCR
Riportiamo anche l’equazione in forma standardizzata:
y =
-2.692 * MSD -1.053 * TIE -1.377 * Xindex + 0.422 * PCR
Risposta predetta - sperimentale
9
Valore predetto
8
7
6
5
4
3
3
4
5
6
7
8
9
Valore sperimentale
Figura 1 – Risposta predetta – sperimentale per il modello scelto
Nel grafico si osserva il confronto tra risposta sperimentale e risposta predetta dal modello. I punti
più vicini alla bisettrice sono quelli meglio predetti. Si osserva un buon accordo del modello con i
dati sperimentali per tutte le molecole:
Molecola
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Valore sperimentale Valore predetto
8.00
7.73
7.15
7.39
7.10
7.05
6.79
6.96
6.92
6.79
6.55
5.94
6.10
6.03
5.96
6.13
5.88
5.91
5.49
5.27
5.19
5.69
5.00
5.10
4.89
4.86
4.00
3.83
Tabella 3 – Valori predetti dal modello
I descrittori coinvolti sono:
•
•
•
•
MSD: mean square distance index (Balaban)
TIE: E-state topological parameter
Xindex: Balaban X index
PCR: ratio of multiple path counts to path counts
I descrittori selezionati appartengono tutti alla categoria dei Topologici e con le nostre conoscenze
non è possibile interpretare il loro significato riguardo all’attività biologica.
L’omogeneità dei descrittori all’interno di ciascuno dei tre gruppi studiati ci offre una visione
parziale della realtà analizzata, limitando la comprensione del fenomeno biologico. Un approccio
differente potrebbe essere quello di creare dei gruppi “misti”, che tengano conto di informazioni di
diverso tipo, per avere una migliore visione d’insieme e un modello predittivo più completo.
Nonostante l’utilizzo di descrittori relativamente omogenei, i risultati ottenuti sono decisamente
buoni. Questo comportamento potrebbe essere spiegato da un lato con la congenericità dei composti
analizzati, dall’altro con l’efficacia degli Algoritmi Genetici nella selezione delle variabili.