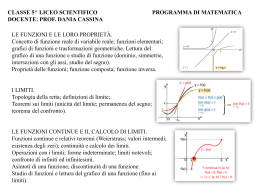
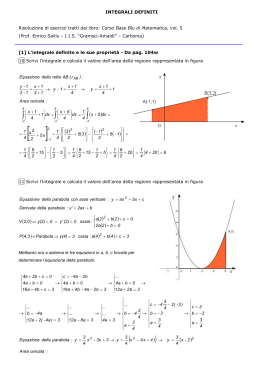
FORMULARIO: tavola degli integrali indefiniti
Definizione
Proprietà dell’integrale indefinito
Integrali indefiniti fondamentali
Integrali notevoli
Integrali indefiniti riconducibili a quelli immediati:
Tecniche di integrazione:
Integrazione per sostituzione
Integrazione per parti
Per il calcolo di integrali del tipo
, talvolta può essere
vantaggioso sostituire alla variabile
d’integrazione x una funzione di
un’altra variabile t, purchè tale
funzione sia derivabile e invertibile.
Ponendo
, da cui deriva
, si ha che:
Si integrano per parti funzioni del tipo P(x)·ex,
P(x)·sin x, P(x)·cos x, eαx·sin βx, eαx·cos βx, dove
P(x) è un polinomio.
Integrali generalizzati più comuni
(integrale di Gauss) o
(Integrale di
Eulero)
(Γ denota la funzione Gamma)
(integrale ellittico),
denota la funzione Beta