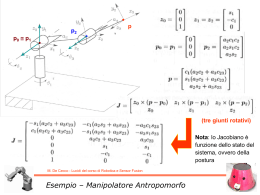
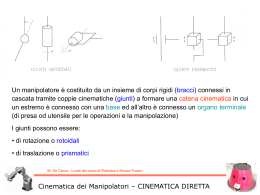
La cinematica differenziale caratterizza i legami tra le velocità dei giunti e la
corrispondente velocità lineare ed angolare dell’organo terminale
Tali legami sono descritti tramite una matrice denominata Jacobiano Geometrico
Se la postura dell’organo terminale è espressa facendo riferimento ad una
rappresentazione in forma minima (angoli di Eulero, Cardano, asse-angolo,
quaternioni, …), è possibile calcolare lo Jacobiano direttamente mediante
differenziazione rispetto alle variabili di giunto. Quello che si ottiene è lo Jacobiano
Analitico (può essere diverso dall’altro)
Lo Jacobiano è utile per:
• l’analisi delle singolarità
• analisi di ridondanza
 p n   J P1 ... J Pj
    J
 n   O1 ... J Oj
• inversione cinematica
 q1 
 ... 
... J Pn   
 q j 

... J On   
 ... 
qn 
• determinazione legame tra forze applicate all’organo terminale e le coppie/forze ai
giunti
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Cinematica differenziale
Manipolatore ad n gradi di mobilità, l’equazione cinematica diretta:
In cui q = [q1 … qn]T è il vettore delle
variabili di giunto
Legami tra le velocità dei giunti e la corrispondente velocità lineare ed
angolare dell’organo terminale:
In forma compatta:
Jacobiano Geometrico funzione delle variabili di giunto q:
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Cinematica differenziale – Jacobiano Geometrico
Si tratterà di derivare la matrice di trasformazione per cui è ora necessario ricavare
come si deriva una componente fondamentale: la matrice di rotazione
La matrice di rotazione in una traiettoria generica sarà funzione del tempo, per cui:


R t   RT t    R t   RT t 



R t   RT t   R t    R t   RT t   R t 

R t    R t   RT t   R t 
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Derivata di una matrice di Rotazione
Se definiamo la SKEW MATRIX:
Ovvero la matrice S(t) è anti-simmetrica (ha gli
elementi sulla diagonale nulli e la parte
triangolare superiore di segno opposto
rispetto alla parte inferiore)
S t   S T t   0
Riprendendo il risultato di prima:


R t    R t   R t   R t 
T

Rt    S T t   Rt 

Rt   S t   Rt 
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Derivata di una matrice di Rotazione
S t    S T t 
Consideriamo un punto p’ solidale ad un corpo sottoposto ad un moto rigido di sola
rotazione
La sua posizione nello spazio è pari a p(t) = R(t) p’
Dunque la derivata:
Che può scriversi:
Del resto sappiamo che la rotazione nel tempo di un vettore
può essere espressa tramite il vettore velocità angolare (t):
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Proprietà della Skew Matrix
Dunque la Skew Matrix descrive il prodotto vettoriale tra il vettore velocità angolare
e la matrice di rotazione:
R t    t   Rt   S t   Rt 
Tale risultato è di importanza fondamentale in quanto trasforma equazioni in cui è
presente la derivata od il prodotto vettoriale in equazioni in cui compare
semplicemente il prodotto tra matrici
Tale artificio è in qualche modo analogo all’uso della trasformata di Fourier nel
campo dell’analisi segnali in quanto si trasformano relazioni poco trattabili (in quel
caso equazioni differenziali nel dominio del tempo) in equazioni algebriche
Poiché la Skew Matrix descrive il prodotto vettoriale tra il vettore velocità angolare e
la matrice di rotazione essa sarà pari a:
 0

S t   S  t    z
  y
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Proprietà della Skew Matrix
 z
0
x
y 

 x 
0 
Si consideri la rotazione elementare attorno all’asse z:
Supponendo  funzione del tempo e che:
 0

S t   S  t    z
  y
 z
0
x
y 

 x 
0 
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Esempio - Skew Matrix
0
 t    0 
 
 
Cerchiamo adesso una proprietà notevole:
Consideriamo di nuovo un punto p’ solidale ad un corpo sottoposto ad un moto
rigido di sola rotazione
pt   Rt   p'
p t   t   Rt   p'
Il risultato del prodotto vettoriale tra due vettori p1 e p2 ruotato di R è pari al prodotto
vettoriale dei due vettori ruotati di R: (scaturisce da semplici considerazioni
geometriche di tipo vettoriale)
Si noti come tale proprietà
pV  p1  p2
R  pV   R  p1    R  p2 
denoti che il prodotto
vettoriale non segue affatto
le regole di composizione
algebrica
Rt   p t   Rt   t   Rt   Rt   p'  S Rt   t   Rt   Rt   p'
p  t   R T  t   S  R  t     t    R  t   R  t   p '  R  t   p '  S    R  t   p '
S t   RT t   S Rt   t   Rt 
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Proprietà della Skew Matrix
In cui, eliminando l’esplicita dipendenza dal tempo:
S    RT  S R     R
S R     R  S    RT
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Proprietà della Skew Matrix
(quando in apice non appare simbolo vuol dire che il vettore è
espresso rispetto alla terna di base)
derivando
p i  p i 1  Ri 1  rii11,i  i 1  Ri 1  rii11,i
i-1
p i  p i 1  vi 1,i  i 1  ri 1,i
i
= 0 giunto rotativo
 0 giunto prismatico
0 terna di base
Espressione della velocità lineare del braccio i in funzione della velocità lineare ed
angolare del braccio i-1
Nota: si omette l’indicazione esplicita dell’apice “0” delle grandezze riferite alla terna di base
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Velocità di un braccio - Lineare
Partendo dalla composizione delle rotazioni e derivando:
Ri  Ri 1  Rii 1
d/dt
Ri  S i   Ri  Ri 1  Rii 1  Ri 1  Rii 1
Ri  S i 1   Ri 1  Rii 1  Ri 1  S ii1,1 i   Rii 1
Dove
ii1,1 i
indica la velocità angolare della terna i rispetto alla i-1 espressa nella terna i-1
Ri 1  S ii11,i  Rii 1  Ri 1  S ii11,i  RiT1  Ri 1  Rii 1  S Ri 1  ii11,i  Ri
Ri  S i   Ri  S i 1   Ri  S Ri 1  ii11,i  Ri
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Velocità di un braccio - Angolare
Ri  S i   Ri  S i 1   Ri  S Ri 1  ii11,i  Ri
i  Ri  i 1  Ri  Ri 1  ii11,i  Ri
  
i
i 1

R


i 1
i 1
i 1,i   Ri  0
i  i 1  i 1,i
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Velocità di un braccio - Angolare
Espressione della velocità
angolare del braccio i in
funzione della velocità
angolare del braccio i-1 ed
angolare relativa tra braccio i
ed i-1
In definitiva:
p i  p i 1  vi 1,i  i 1  ri 1,i
i  i 1  i 1,i
Da cui si nota come l’effetto di un
giunto j si ripercuota solamente sui
giunti successivi (come del resto
doveva essere trattandosi di catene
cinematiche aperte)
Vogliamo adesso calcolare lo Jacobiano definito come:
(generalizzando al caso rotativo e prismatico)
 p n   J P1 ... J Pj
    J
 n   O1 ... J Oj
 q1 
 ... 
... J Pn   
 q j 

... J On   
 ... 
qn 
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Calcolo dello Jacobiano
Mediante moltiplicazione matriciale:
 p n   J P1  q1  ...  J Pj  q j  ...  J Pn  qn 
    J  q  ...  J  q  ...  J  q 
Oj
j
On
n
 n   O1 1
Nota:
dqj/dt è uno scalare
JPj e JOj sono vettori 3x1
In cui, evidentemente:
J Pj
J Oj
rappresenta il contributo della derivata della variabile di giunto j alla
velocità lineare dell’end-effector (con tutti gli altri giunti fermi)
rappresenta il contributo della derivata della variabile di giunto j alla
velocità angolare dell’end-effector (con tutti gli altri giunti fermi)
Il ché vuol dire che per determinare gli elementi dello Jacobiano si può
applicare il principio di sovrapposizione degli effetti (del resto l’operazione
di derivazione porta ad una approssimazione lineare)
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Calcolo dello Jacobiano
Calcolo di
J Pj
:
p i  p i 1  vi 1,i  i 1  ri 1,i
Poiché l’effetto di un giunto j si
ripercuote solamente sui giunti
successivi:
pn  p j 1  v j 1, j  ...  vn 1,n   j 1  rj 1, j  ...  n 1  rn 1,n
pn  v j 1, j  ...  vn 1,n   j 1  rj 1, j  n 1  rn 1,n
Nel giunto prismatico :
v j 1, j  d j  z j 1
q  d
j
j
Nel giunto rotoidale :
 j 1, j   j  z j 1
q j   j
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Calcolo dello Jacobiano – Contributo Lineare
Solo il braccio j si
muove, quindi alcuni
termini si annullano
Calcolo di
J Pj
:
= 0 poiché gli altri giunti
prismatici sono fermi
= 0 poiché non ci sono
giunti rotoidali in azione
pn  v j 1, j  ...  vn 1,n   j 1  rj 1, j  ...  n 1  rn 1,n
p n  d j  z j 1
Nel giunto prismatico :
v j 1, j  d j  z j 1
q  d
j
j
J Pj  z j 1
Prismatico
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Giunto Prismatico – Contributo Lineare
Calcolo di
J Pj
i  i 1  i 1,i
:
= 0 poiché non ci sono
giunti prismatici in azione
Tutte le velocità angolari sono uguali
in quanto si ha l’effetto del giunto
rotoidale anche sugli altri giunti
p n  v j 1, j  ...vn1,n   j 1  rj 1, j  ...  n1  rn1,n
p n   j 1  rj 1, j  ...   j 1  rn1,n   j 1  rj 1, j  ...  rn1,n    j 1  rj 1,n

p n   j 1   pn  p j 1    j  z j 1  p n  p j 1
Nel giunto rotoidale :
 j 1, j   j  z j 1
q j   j

J Pj  z j 1   pn  p j 1 
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Giunto Rotoidale – Contributo Lineare
Rotoidale
Calcolo di
J Oj
i  i 1  i 1,i
:
= 0 poiché solo il giunto
i_esimo è in azione
Nel giunto prismatico :
 j 1, j  0
q j  d j
J Oj  0
Prismatico
Nel giunto rotoidale :
n   j 1, j
 j 1, j   j  z j 1
q j   j
J Oj  z j 1
Rotoidale
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Calcolo dello Jacobiano – Contributo Rotazionale
In definitiva:
 z j 1   pn  p j 1 
Jj 

z j 1


Rotoidale
 z j 1 
Jj  
 0 
Che dipendono da:
 z j 1
pn
p j 1 
Prismatico
… e quindi dalla postura del robot
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Calcolo dello Jacobiano
Tali relazioni consentono il calcolo dello Jacobiano in maniera semplice e
sistematica sulla base delle relazioni cinematiche dirette, in particolare:
0
0
z j 1  R 0j 1  0  R10 q1   ...  R jj23 q j 2  R jj12 q j 1  0
 
 
1
1
0
0
0
0
pn  An0   1...3  A10 q1   ...  Ann12 qn 1   Ann 1 qn    1...3
0
0
 
 
1
 
1
0
0
0
0
p j 1  A0j 1   1...3  A10 q1   ...  Ajj23 q j 2   Ajj12 q j 1    1...3
0
0
 
 
1
 
1
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Calcolo dello Jacobiano
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion