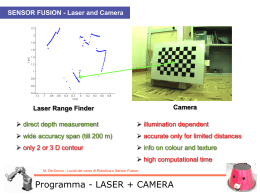
… se si impiega anche la conoscenza del modello del sistema, si
perviene al
Filtro di Kalman
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman
È possibile costruire un filtro ricorsivo che prenda in ingresso tutte le
misure disponibili e combini tra loro le informazioni contenute in ciascun
dato, compresa la conoscenza del modello dello strumento che lo ha
fornito
Il temine ricorsivo è fondamentale per un’implementazione al calcolatore
del filtro di Kalman, esso indica infatti che l’algoritmo non richiede la
memorizzazione e la rielaborazione di tutta la storia dei dati ogni volta che
è disponibile una nuova misura
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman
Modello di stato del sistema
Modello di osservazione
Fonti di incertezza
sul sistema
Fonti di incertezza
sulle misure
Stato del sistema
(desiderato, ma
non noto)
Controlli
Sistema
Strumenti
di misura
Misure (Osservazioni)
Stima dello stato basata
su modello del sistema
La conoscenza degli ingressi (controlli) e uscite
(misure) può essere utilizzata per effettuare una
stima dello stato del sistema
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman
Filtro di Kalman
Stima Ottima dello
Stato del Sistema
Le fonti di incertezza sul modello del sistema o incertezza di modello
derivano dalla non completa conoscenza di tutte le variabili che influiscono
sulla sua dinamica e da scostamenti dal modello matematico spesso
semplificato.
Le fonti di incertezza sulle misure comprendono:
- la non perfetta conoscenza di quali sono le relazioni tra le variabili di stato
e le uscite misurate (incertezza di modello degli strumenti) – effetti
principalmente modificanti
- l’incertezza dovuta agli errori casuali e sistematici – effetti principalmente
interferenti
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman – fonti incertezza
Sotto le seguenti ipotesi il filtro di Kalman fornisce una stima ottima
dello stato:
- il sistema sia descritto da un modello lineare
- il rumore associato al sistema e alle misure sia bianco e Gaussiano
(ovvero a media nulla, con densità di potenza
spettrale distribuita uniformemente su tutta la banda
di frequenze e con distribuzione di probabilità
Normale, e non correlato nelle sua realizzazione
ovvero non c’è correlazione tra un suo campione ed il
successivo!)
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman - ipotesi
Il modello di sistema lineare è giustificabile per varie ragioni.
- spesso un modello lineare si adatta bene allo scopo
- in presenza di non linearità, l’approccio ingegneristico più utilizzato è
quello della linearizzazione del modello attorno a una qualche
configurazione del sistema, ad esempio un punto o una traiettoria
- la teoria dei sistemi lineari è molto più completa e pratica di quelli non
lineari
Esistono dei metodi per estendere l’applicazione del filtro di Kalman ai
sistemi non lineari qualora essi dovessero rivelarsi inadeguati: Filtro di
Kalman esteso
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman – ipotesi di linearità
L’ipotesi di rumore bianco implica che i valori di rumore non sono correlati
tra di loro nel tempo.
In pratica, se si conosce quanto vale il rumore all’istante attuale, ciò non
aggiunge nessuna informazione ai fini di una previsione su quale sarà il
suo valore in un altro istante.
Inoltre un rumore bianco ha uno spettro con uguale densità di potenza per
tutte le frequenze, ciò implica che un tale segnale ha potenza infinita!,
pertanto un rumore bianco non può esistere in natura
Poiché però ogni sistema fisico ha una banda passante limitata nello
spazio delle frequenze ed è tipicamente affetto da un rumore a larga
banda, dal punto di vista del sistema è equivalente ad assumere che vi sia
rumore bianco
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman – ipotesi di rumore bianco
Se invece all’interno della banda passante del sistema il rumore non ha
densità spettrale uniforme, oppure è correlato nel tempo, attraverso un
filtro aggiuntivo è possibile riprodurre, partendo da un rumore bianco,
qualsiasi forma di rumore correlato (il filtro consiste in un sistema lineare
chiamato “shaping filter”).
Tale filtro viene poi aggiunto alla dinamica del sistema.
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman – ipotesi di rumore bianco
Mentre l’attributo “bianco” per un rumore è riferito alle sue caratteristiche
temporali (o di frequenza), l’attributo “Gaussiano” è riferito alla sua
ampiezza. Cioè, per ogni singolo istante temporale, la densità di probabilità
dell’ampiezza di un rumore Gaussiano ha la nota forma di una campana.
Questa assunzione è giustificata in senso fisico dal fatto che, tipicamente,
vi è un gran numero di piccole sorgenti che contribuiscono a creare il
rumore di misura.
Questo fenomeno è descritto dal teorema del limite centrale:
all’aumentare del numero di variabili casuali indipendenti che si sommano
tra loro, qualora non ve ne sia nessuna preponderante, qualunque sia la
distribuzione di probabilità di ciascuna, la distribuzione di probabilità della
somma tende ad essere quella Gaussiana
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman – ipotesi di rumore gaussiano
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman – modello sistema lineare
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman – modello sistema discreto
L’ipotesi di base per il filtro di Kalman in cui si assume che il rumore del processo di
evoluzione dello stato e il rumore di misura siano a media nulla e temporalmente
scorrelati si traduce rispettivamente con le equazioni
E vk   E wk   0, k
E v (i )v ( j )T    ij  Q (i ),
xˆ ( k | k  1)
E w(i ) w( j )T    ij  R(i )
è la stima dello stato all’istante k condizionata alle sole
informazioni ottenute fino all’istante k-1 è detta previsione di un passo in avanti.
Tale simbologia viene impiegata da ora in avanti
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Si assume che al passo k-esimo siano noti i seguenti parametri:
la stima
xˆ ( k  1 | k  1)
la covarianza condizionata
P(k  1 | k  1)
Si calcola la previsione:
xˆ (k | k  1)  F (k ) xˆ (k  1 | k  1)  B(k )u(k )
P(k | k  1)  F (k ) P(k  1| k  1) F T (k )  G(k )Q(k )G T (k )
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Si calcola l’aggiornamento:
Scarto tra misura e previsione
della misura
xˆ (k | k )  xˆ (k | k  1)  W (k )[ z (k )  H (k ) xˆ (k | k  1)]
P(k | k )  [1  W (k ) H (k )]P(k | k  1)[1  W (k ) H (k )]T  W (k ) R(k )W T (k )
Dove, la matrice di Kalman:
W (k )  P(k | k  1) H (k )[ H (k ) P(k | k  1) H T (k )  R(k )]1
NOTA:
• la previsione è generata dal filtro utilizzando il modello di evoluzione del misurando
• l’aggiornamento fa uso del modello di misura
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Stima iniziale
Modello del sistema
Previsione
xˆ k | k 1 Pk | k 1
xˆ k | k Pk | k

Aggiornamento
Misura
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman – schema ricorsivo
Si calcoli l’aggiornamento per un semplice caso scalare:
ipotesi :
P ( k | k  1)   x2
R ( k )   z2
xˆ F  xˆ  W [ z  xˆ ]
H 1
Dove, la matrice di Kalman:
 x2
W 2
 x   z2
 x2
 x2
 x2
xˆ F  xˆ  2
[ z  xˆ ]  xˆ  2
z  2
 xˆ 
2
2
2
x z
x z
x z

 x2
 x2 
 z  1  2
 xˆ 
2
2
2 
x z
 x z 
 x2
 z2
z  2
 xˆ
2
2
2
x z
x z
(combinazione Bayesiana della misura z e della previsione x)
Si noti anche che se misura e previsione sono uguali non c’è aggiornamento
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Filtro di Kalman – filtraggio Bayesiano!
Abbiamo visto i fondamenti dell’applicazione del teorema di
Bayes e del filtro di Kalman, per la combinazione delle
informazioni, ora vediamo un esempio concreto di SENSOR
FUSION!
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Teorema di Bayes
1° STEP (a & b)
1° STEP (c)
• Odometers
• Laser Triangulating Scanner
2° STEP
• Gyro
- Limited repeatability (motion,
poor environment, …)
- Smooth updates
- Drift
1 & 2° STEP:
- No drift
Smooth updates &
no drift
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Esempio di applicazione (veicoli mobili)
X
X
E
n
L
n
C
C
X  C C  C
E
n
E
n
C  C C  C
F
n
E
n
E
n
X
F
n
C
Sensor
Fusion
E
n
X
F
n
L
n
E
k
C
 X
C
L 1
n
L 1
n
L
n
F
n
Delay
Comp.
E
k
X
C
n k
 C C  C
L
n
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Esempio di applicazione
L
n
E
n
C

L 1
n
C
n k
X nE
Si fondono i dati all’istante Ts e poi si somma la variazione di posa e
l’accumulo di covarianza
C
Xnk
 XnF  X kE
Laser Scan data
CnCk  CnF  CkE
Tl

LS_NAV computation time
Ts2 = (n+m)Tl
Data Fusion
To
Odometric estimation
Ts1 = nTl
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Esempio di applicazione

time
X kE
Tcomp = nTl+ kTo
L’incertezza del LS_NAV è funzione della velocità angolare che provoca un
degrado della mappa dovuto al moto del veicolo sovrapposto al moto di
scansione del raggio laser

C  C0  1    v
L
n
2



 1    


2





v 
: velocità lineare ed angolare
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Esempio di applicazione – stima incertezza laser
LS NAV,Odometric,Fused Trajectory
searching range input
LS NAV estimated pose
LS NAV first guess pose
odometric traj.
fused traj.
0.6
0.4
0.2
A
]
m
[
Y
0
-0.2
-0.4
B
C
-0.6
-0.8
-1
1.4
1.6
1.8
2
2.2
2.4
2.6
2.8
3
3.2
3.4
X [m]
In evidence initial guess of pose and searching fields of possible solutions
derived from computed covariance given as an input to the LS_NAV algorithm
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Esempio di applicazione
LS NAV and Fused Attitude. Zoom
fused attitude
LS NAV attitude
fused attitude uncertainty (95%)
2
1
0
-1
LS NAV and Fused Attitude
]
g
e
d
[
fused attitude
LS NAV attitude
fused attitude uncertainty (95%)
10
-2
-3
-4
5
-5
0
-6
-5
-7
]
g
e
d
[
-10
-8
-15
76
78
80
Odom. cycle time
82
-20
-25
-30
-35
50
60
70
80
90
100
110
Odom. cycle time
Assetto fuso e relativo intervallo di confidenza
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Esempio di applicazione – assetto fuso
84
86
Trajectories comparison
0.5
Encoder
Sensor Fusion
0
-0.5
]
m
[
-1
Y
-1.5
-2
-2.5
-0.5
0
0.5
1
1.5
2
X[m]
2.5
3
3.5
4
4.5
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Esempio di applicazione – compensazione deriva
SLAM
Simultanea localizzazione e
mappatura di veicoli autonomi in
ambiente non strutturato
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Strutturato:
-
Ingegnerizzazione dell’ambiente
Bassa flessibilità
Conoscenza a priori della mappa
Non strutturato:
-
Non necessita di infrastrutture
Alta flessibilità
Costruzione mappa in tempo reale
Passi fondamentali per interagire con
ambiente non-strutturato:
- navigazione e propagazione incertezza mediante
sistemi di misura autocontenuti
- autolocalizzazione mediante landmark naturali
- fusione tra navigazione incrementale e quella riferita
all’ambiente
- mappatura dell’ambiente stesso
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Ambiente in cui il robot opera
- Veicolo a guida differenziale
- Sistema di acquisizione PXI LabView RTOS
- 2 Encoder incrementali :
no:4000
- Laser a scansione IR
[SICK PLS-101]
:
Tempo di volo
Risoluzione angolare max: 0.5°
Campo di scansione: (0°,180°)
1
Distanza massima:
D 50cTm
2
Accuratezza = f(orientazione,materiali)
Parametro
Incertezza
Range
distanze
5 cm
7-50 m
angoli
0.1 °
0-180 °
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Veicolo e strumentazione
Equazione cinematica di ricorrenza:
xk 1  xk  
nRk  RR  nLk  RL
 cos  k 
n0 rid
yk 1  yk  
nRk  RR  nLk  RL
 sin  k 
n0 rid
 k 1   k  2
Parametri incerti:
C k =
Parametro
nRk  RR  nLk  RL
b  n0 rid
Valore
Nominale µ
Deviazione
standard σ
RR
89.50 mm
0.14 mm
RL
89.50 mm
0.14 mm
L
89.50 mm
0.5 mm
b
89.50 mm
0.5 mm
Equazione cinematica di ricorrenza(PLS):
xls ,k 1  xr ,k 1   ls  cos  k 
yls ,k 1  yr ,k 1   ls  sin  k 
POSA con INCERTEZZA
8
 ls ,k 1   k  ls
7
Covarianza della posa:


=  y
 x

2
xk
C Xk
 xy
 yy2
 y
θLS
 x 

 y 
  
[x,y,δ]
δ
b
αi,j
6
5
)
m
(
4
Y
3
2
1
Propagazione incertezza:
CXk+1 = CXk + J φk  Cωk  J φk
0
-1
-1
0
1
T
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Propagazione incertezza odometrica
2
3
X (m)
4
5
6
7
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Mappatura
scala
scala
p
A
ringhiera
A
W
Sono stati fatti compiere al
veicolo 2 giri del laboratorio
per verificare i metodi
sviluppati
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
S
AGV
S
S
S
A
Sono stati fatti compiere al veicolo 2 giri del laboratorio per verificare i
metodi sviluppati: filmato che mostra l’ambiente, il veicolo ed una
tecnica di determinazione del percorso mediante scansioni e gestione del
grafo delle profondità
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion