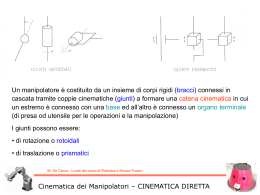
Si era visto a proposito dell’inversione della cinematica tramite cinematica diretta,
che il problema ammette soluzioni in forma chiusa solo per strutture di
manipolazione semplici
Sorgono immediatamente problemi quando:
• il manipolatore ha una struttura complessa (non facilmente risolvibile o soluzioni
non in forma esplicita)
• è ridondante (infinite soluzioni)
• in corrispondenza di posture singolari
v  J  q
… ma adesso abbiamo un nuovo strumento: la Cinematica Differenziale che ci
fornisce la relazione tra la velocità ai giunti e le velocità nello spazio operativo (in
funzione della postura)
Dunque perché non invertire la relazione cinematica differenziale ed integrare?
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
Basterà assegnare la traiettoria specificando v(t) e le sue condizioni iniziali di
posizione ed assetto nello spazio operativo e di postura nello spazio dei giunti e
determinare q(t) tramite:
q  J 1  v
t
q(t )   q    d  q(0)
0
L’integrazione potrà essere fatta nel tempo discreto (tramite ad esempio la formula
di Eulero) in forma ricorsiva ed implementata quindi in tempo reale:
q(tk )  q(tk 1 )  q (tk 1 )  TC
q(tk )  q(tk 1 )  J 1 q(tk 1 )   v(tk 1 )  TC
qk  qk 1  J k11  vk 1  TC
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
… ma lo Jacobiano deve essere quadrato e di rango pieno
Se il manipolatore è ridondante (r < n) tale condizione non è verificata (J è
rettangolare bassa) ed in generale esistono più soluzioni
Per risolvere il problema della determinazione della soluzione tra tante, occorre
specificare criteri di scelta
E quindi trasformare il problema in un problema di ottimizzazione vincolata (in
cui ci sarà un funzionale da minimizzare che determinerà la scelta):
ad esempio si cerca quella soluzione che minimizza il funzionale:
(ovvero le velocità ai giunti)
Con il vincolo:
v  J  q
il funzionale è quadratico con matrice W simmetrica e definita positiva (ovvero il
funzionale è sempre > 0 per ogni valore di dq/dt ≠ 0)
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
Il problema di minimo vincolato può essere risolto con i moltiplicatori di Lagrange
mediante il funzionale modificato
T è il vettore 1 x r dei moltiplicatori che permette di incorporare il vincolo nel
funzionale (non modificandolo in quanto il vincolo è una equazione pari a zero)
il funzionale (funzione di dq/dt e ) viene derivato per determinarne il minimo (il
funzionale è una forma quadratica associata ad una matrice definita positiva, nel
caso scalare è come se fosse a·x2 il cui minimo si determina mediante semplice
derivazione)
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
(con il suggerimento di Bertolazzi)

1  T
1 T 

T
g  q,   
q

Wq

q
W
q


J


q 


q
2 q
2
q
q
1  T
1 T 
q

Wm

mW
q  T J  I  m  q 


2 q
2
q
T
W

W
1  T
1 T
q  Wm   m W  I   T J 

Matrice simmetrica
2 q
2
È uno scalare quindi uguale al suo trasposto
1 
1 T
T
m
Wq

m W  T J 


2 q
2
1 T
1
ÝT W  T J  0
Ý J T   0
m W  mT W   T J  mT W   T J
m
Wm
2
2
WqÝ J T   0

T
q  W 1 J 

M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion

Inversione differenziale della Cinematica
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
Nel caso in cui W = I la soluzione impiega la pseudo-inversa J†, e la soluzione
trovata è quindi quella che minimizza la norma di tutte le velocità ai giunti senza
distinzione
1
g q 
Se invece:
2
qT  q
 9 0
W 

0
1


In questo caso la prima componente delle velocità dei giunti viene minimizzata in
maniera più marcata rispetto alla seconda (1/3)
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
Come visto in precedenza, evitare le configurazioni di singolarità è un requisito
fondamentale nella pianificazione della traiettoria
Dunque perché non specificare un funzionale in cui la soluzione si avvicini il più
possibile ad una soluzione in grado di evitare le singolarità?
Trovata q0 la traiettoria delle variabili di giunto in grado di evitare le singolarità
Si stabilisce il seguente funzionale da minimizzare:
Con il vincolo:
(in maniera analoga a quanto visto prima)
… che risulta essere proprio della forma:
q  q *  P  q0
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
Se infatti:
P  I  J  J
Si ha che:
q0 : J  P  q0  J  I  J   J  q0 

J  I  J  J  J
T

T 1
 
 J  q0  J  J  J  J  J
T

T 1

 J  q0 
J  J  q0  0
Ovvero P è proprio il proiettore sul nullo di J
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
Rimane solo da determinare q0 in modo tale che le singolarità vengano evitate.
Definita la funzione:
Basta scegliere:
Con k0 > 0
Spiegazione: la funzione w(q) è pari a zero in corrispondenza delle singolarità,
cresce man mano che ci si allontana dalle configurazioni singolari
Dunque scegliere q0 lungo il gradiente vuol dire allontanarsi dalle
configurazioni non desiderate!
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Come evitare le SINGOLARITA’
… se si vuole evitare le situazioni di fine-corsa (anche esse generalmente singolari)
che creano situazioni di limitazione alla destrezza del manipolatore
La w(q) la si definisce come segue:
wq
qi
qi
qim
qiM
dove:
 qiM e qim rappresentano la massima e minima escursione alla rispettiva variabile
di giunto qi

qi
il valore medio della corsa
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Come evitare situazioni di FINE CORSA
… se si vuole evitare ostacoli
La w(q) la si definisce come segue:
dove:
 o è il vettore posizione di un opportuno punto dell’ostacolo (ad esempio il centro)
 p è un opportuno punto (od una collezione di punti, oppure …) della struttura
come ad esempio l’organo finale in operazioni di inserimento
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Come evitare OSTACOLI
… siamo sicuri che determinare lo stato delle variabili di giunto mediante una
operazione di integrazione non crei dei problemi?
q(tk )  q(tk 1 )  J
1
 q(tk 1 )   v(tk 1)  TC   (tk 1)
NO, LA DERIVA !!!
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
Per ovviare all’inconveniente della deriva che porta a seguire traiettorie che si
discostano in modo pressoché proporzionale con il tempo dalla traiettoria
desiderata, occorre considerare l’errore nello spazio operativo:
e  t   xd  t   x  t 
Dove xd(t) è la traiettoria desiderata ed x(t) è la traiettoria calcolata mediante
inversione differenziale della cinematica
Derivando rispetto al tempo:
e  xd  x
Che, mediante la scelta
e  xd  J  q   q
q  J 1  q   xd    t 
, conduce a problemi di deriva
in quanto il termine di incertezza  è sempre presente (ad esempio errori numerici
o di modellazione)
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
Dunque bisogna scegliere l’andamento di dq/dt che tenga conto dell’errore nello
spazio operativo e possibilmente che presenti una dinamica stabile dell’errore in
modo che converga a zero:
e  K  e
Con K definita positiva ed autovalori tutti > 0
Ricordando:
e  xd  J  q   q
 K  e  xd  J  q   q
q  J 1  q   xd
≠
q  J 1  q    xd  K  e 
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
Quale è lo schema a blocchi dinamico che implementa tale metodo di integrazione
basato sulla retroazione dall’errore nello spazio operativo?
Impiegare i blocchi sottostanti:
Costante di retroazione
Iacobiano inverso
Integratore
Cinematica diretta
(Ingressi)
(uscita)
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
Serve un richiamo di Simulink?
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Quale è lo schema a blocchi dinamico che implementa il metodo di integrazione
basato sulla retroazione dall’errore nello spazio operativo, di seguito riportato?
q  J 1  q    xd  K  e 
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
Se il manipolatore è ridondante la J non è quadrata e non è possibile invertirla,
per cui si ha la generalizzazione:
P: proiettore nel nullo
Stessa formula con il solo
impiego della pseudo-inversa
Parte dedicata al controllo dei
moti interni indirizzati ad evitare
le singolarità, gli ostacoli, i
finecorsa, a minimizzare
l’energia, etc
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
A volte invertire lo Jacobiano può risultare non ottimale dal punto di vista
computazionale (nel caso di microprocessori a scarsa velocità/memoria/potenza di
calcolo, caso sempre meno frequente ma ancora possibile in talune applicazioni
industriali)
Dunque si vuole evitare l’inversione
… e quindi perché non retroazionare semplicemente (con una semplice operazione
di trasposizione) rispetto all’errore?
J q  q  J q  J T q  K  e
x  J  q   J T  q   K   xd  x 
In questo caso si ha una variazione dello stato nello spazio operativo solo se
l’errore è diverso da zero. Equivale ad una azione proporzionale.
Si dimostra che il metodo è asintoticamente stabile (mediante il criterio di Liapunov)
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
Quale è lo schema a blocchi dinamico che implementa tale metodo di integrazione
basato sulla retroazione dall’errore nello spazio operativo?
q  J T  q   K   xd  x 
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica
M. De Cecco - Lucidi del corso di Robotica e Sensor Fusion
Inversione differenziale della Cinematica