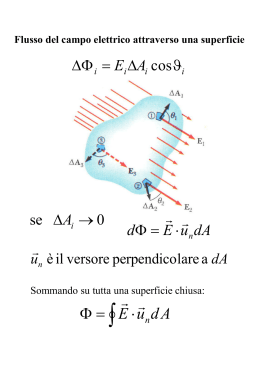
Campo elettrico e potenziale di un disco uniformemente carico
σ=
q
S
densità superficiale di carica
Considero l’anello di raggio r e spessore dr
•calcolo l’anello
•sommo sugli anelli
⇒ ho due integrazioni
dq = σdA = σ2πrdr
σ 2πrdr
z
dEanello =
4πε 0 r 2 + z 2
σz
E ∫ dEanello =
4ε 0
Σ
(
∫ (r
R
0
2
σz
2rdr
=
4ε 0 r 2 + z 2
)
(
+ z ) (2 r )dr
3
2
3
2 − 2
)
3
2
Ricordiamo che
x m +1
∫ x dx = m +1
x = z 2 + r 2 dx = 2rdr m = -
m
3
2
Allora troviamo
σz (z + r )
=
−1
4ε 0
2
2
Edisco
Edisco
2
−1
R
σz
=
2ε 0
2
0

σ 
z

=
1−
2ε 0  (z 2 + R 2 )1 2 


Per R ⇒ ∞
Edisco


1
1
−
+ 
1
 (z 2 + R 2 ) 2 z 


z ≥0
σ
⇒ E piano infinito =
2ε 0
Per z ⇒ 0
E disco
σ
⇒ E piano infinito =
⇒ vicino al disco il campo è quello di un piano ∞
2ε 0
Passiamo ora al calcolo del potenziale
1 dq
1 σ 2πrdr
dV =
=
4πε 0 r
4πε 0 z 2 + r 2 1 2
(
)
σ
r
V = ∫ dV = ∫
2ε 0 z 2 + r 2
V (0)
0
V ( R)
R
(
Per R ⇒ ∞
Per z ⇒ 0
σ
dr =
1
2
2ε 0
)
V ⇒∞
σR
V⇒
2ε 0
(z
2
+ R2 − z
)
z≥0
Campo elettrico creato da una carica uniformemente distribuita su di un
piano conduttore infinito (σ
σ > 0)
Le linee di forza del campo elettrico sono ⊥ al
piano carico
Prendiamo come superficie gaussiana un cilindro
che attraversa la superficie carica ed è ⊥ ad essa e
calcoliamo il flusso totale
Φ Er = Φ Er (S1 ) + Φ Er (sup. lat.) = ES + 0
Φ Er = ES =
σS
ε0
q = σS
Infine troviamo
σ
E=
ε0
Il campo elettrico sulla superficie di un conduttore non dipende dalla
distanza dal piano: campo uniforme
Consideriamo ora una lamina infinita isolante uniformemente carica con
densità σ > 0
Il campo elettrico è ⊥ alla lamina ed è uscente
La superficie gaussiana che consideriamo è
sempre un cilindro ⊥ alla superficie stessa
Le linee di forza intersecano la superficie
gaussiana da una parte all’altra
Φ Er = Φ Er (S1 ) + Φ Er (S 2 ) + Φ Er (sup.lat.) = ES + ES + 0
Φ Er = 2 ES =
e quindi
σS
ε0
q = σS
σ
E=
2ε 0
Il risultato vale per punti a distanza finita
dalla lamina
Consideriamo ora due piastre conduttrici uniformemente cariche e con
carica opposta con densità σ = 2σ
σ1 , il campo elettrico è nullo all’interno
delle due piastre e appena al di fuori di esse vale
E+ =
σ
per la piastracon carica positiva
2ε 0
E− = −
σ
per la piastracon carica negativa
2ε 0
Notiamo che il campo elettrico è uscente dalla piastra con carica positiva
ed entrante nella piastra con carica negativa
Se ora avviciniamo le due piastre dobbiamo combinare i due campi
elettrici
Nella zona 1 abbiamo
σ
σ
E1 = − E+ + E− = −
+
=0
2ε 0 2ε 0
Nella zona 2 troviamo
1
2
3
E2 = E+ + E− =
σ
σ
σ
+
=
2ε 0 2ε 0 ε 0
Nella zona 3 infine è
E2 = E+ − E− =
σ
σ
−
=0
2ε 0 2ε 0
In conclusione abbiamo creato un campo elettrico uniforme confinato
nello spazio compreso tra le due lamine conduttrici. Notiamo che
passando attraverso ad una superficie carica il campo subisce una
discontinuità pari a σ/εε0, proprietà sempre valida
Esaminiamo il potenziale associato ad un dipolo elettrico
Determiniamo il potenziale del dipolo nel punto P,
esso sarà la somma del potenziale V+ dovuto alla
carica positiva e V- dovuto alla carica negativa
VTOT ( P) = V+ ( P) + V− ( P) =
1 q q
q r− − r+
 −  =
4πε 0  r+ r−  4πε 0 r− r+
Nella realtà i dipoli sono molto piccoli e quindi
possiamo assumere che r >> d, allora
r− − r+ ≈ d cos ϑ
V=
r+ r− ≈ r 2
q d cos ϑ
4πε0 r 2
1 p cos ϑ
V=
4πε0 r 2
Ora che abbiamo determinato il potenziale del dipolo elettrico, possiamo
calcolare il campo elettrico del dipolo in ogni punto dello spazio usando
le coordinate polari r e θ
Eθ E
uθ
ur
θ
P
Er
p
∂V
2 p cos ϑ
Er = −
=
∂r 4πε 0 r 3
ds = rdϑ
1 ∂V p sin ϑ 1
Eϑ = −
=
r ∂ϑ
4πε 0 r 3
Note sull’energia potenziale
Analizziamo ora l’energia potenziale associata ad un sistema di più
cariche. Fino a qui abbiamo parlato di U solo per una carica q che si
trova in un campo elettrico E generato da altre cariche, ora ci chiediamo
invece qual è l’energia potenziale del sistema di cariche che genera il
campo.
Costruiamo il nostro sistema di cariche, prendendo ciascuna carica e
portandola dall’infinito alla sua posizione finale, (le cariche sono in
quiete sia all’infinito che nella posizione finale f)
− ∆U = −(U f − U ∞ ) = L∞ → f
Il sistema più semplice è quello costituito da due cariche q1 e q2.
Prendiamo la carica q1 e la portiamo dall’infinito alla sua posizione finale
f1, per fare questo non variamo alcuna energia potenziale in quanto non
abbiamo ancora un campo elettrico e quindi non facciamo lavoro
Prendiamo ora la carica q2 che si trova in quiete all’infinito e la portiamo
alla posizione finale f2 situata ad una distanza r da q1. Abbiamo bisogno
di applicare una forza F = -q2E che compia il lavoro L necessario a
costruire il sistema, al termine del processo il sistema ha ricevuto energia
(il lavoro fatto) e l’ha immagazzinata sotto forma di energia potenziale
U=
1 q1q2
= q2V
4πε 0 r
Esempio
Vogliamo determinare l’energia potenziale
elettrostatica del sistema di cariche rappresentato
in figura
d = 12 cm, q1 = +q, q2 = -4q, q3 = +2q, q = 150 nC
Sappiamo già che per posizionare la carica q1 non dobbiamo compiere
alcun lavoro, quindi portiamo la carica q2 a distanza d da q1
1 q1q2
L12 = U12 =
4πε 0 d
Prendiamo ora q3 e la portiamo a distanza d sia da q1 che da q2, per fare
ciò dobbiamo compiere due lavori in quanto abbiamo due campi, quello
generato da q1 e quello generato da q2, pertanto
1 q1q3
1 q2 q3
L = L13 + L23 = U13 + U 23 =
+
4πε0 d
4πε0 d
L’energia potenziale elettrostatica del sistema così costruito sarà la
somma delle energie elettrostatiche accumulate nel sistema durante la
sua costruzione
U = U12 + U13 + U 23
1 q1q2
1 q1q3
1 q2 q3
=
+
+
4πε 0 d
4πε 0 d
4πε 0 d
10 q 2
U=
= −17 mJ
4πε0 d
L’energia potenziale elettrostatica negativa indica che il sistema si rompe
solo se dall’esterno gli si fornisce un’energia pari a 17 mJ, si dice anche
che il sistema è legato
L’energia potenziale elettrostatica così calcolata non dipende dall’ordine
con cui vengono considerate le cariche, ma solo dalle interazioni fra le
coppie di cariche, interazioni che vanno considerate una volta sola per
coppia.
L’energia potenziale elettrostatica appartiene al sistema di cariche
1
U=
4πε 0
∑
i< j
qi q j
rij