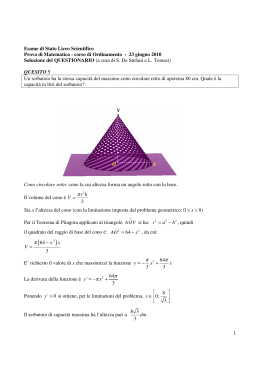
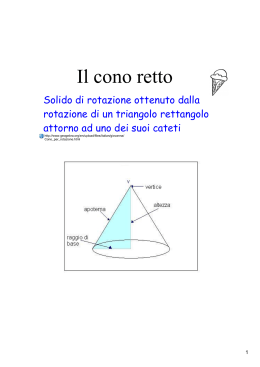
Consideriamo il triangolo
rettangolo ABC e facciamolo
ruotare di 360° attorno a un
suo cateto. La parte di spazio
che esso occupa nelle varie
posizioni costituisce un solido
di rotazione chiamato cono
circolare
retto
e
semplicemente cono.
C
A
B
C
A
B
Diciamo che:
altezza
Il cono è un solido ottenuto dalla rotazione completa di
un triangolo rettangolo attorno a un suo cateto.
Il cateto attorno a cui gira è l’asse di rotazione e
rappresenta l’altezza del cono, l’ipotenusa è la generatrice
e si chiama apotema del cono, l’altro cateto è il raggio del
cerchio che forma la base del cono.
apotema
raggio
La superficie laterale del
cono corrisponde alla
superficie di un settore
circolare il cui arco è
congruente alla
circonferenza di base
del cono e il cui raggio è
congruente all’apotema.
Poiché l’area di un settore circolare si può
calcolare moltiplicando la lunghezza dell’arco
per la misura della lunghezza del raggio e
dividendo tale prodotto per due, potremo dire
che:
Circonferenza di base
L’area della superficie laterale di un cono si ottiene moltiplicando la misura della
lunghezza della circonferenza di base per la misura della lunghezza dell’apotema
e dividendo tale prodotto per 2.
In formule possiamo
scrivere:
Ca
 Sl  ra
2
( formula diretta )
Sl 
Circonferenza di base
Sl
Sl
a
a
r
( formule inverse)
r
St  Sl  Ab ovvero St  ra  r 2
Per quanto riguarda il calcolo del volume di un cono,
confrontiamolo con quello di un cilindro, avente la stessa
base e la stessa altezza del cono, usando due solidi cavi. Ci
accorgeremo che per riempire il cilindro di sabbia usando il
cono occorrerà ripetere tre volte l’operazione.
Possiamo quindi dire che:
Il cono è equivalente a un
terzo di un cilindro avente
base e altezza congruente
rispettivamente alla base e
all’altezza del cono.
In formule:
Ab  h
r 2 h
V 
V 
3
3
( formula diretta )
r
3V
h
h
3V
( formule inverse)
2
r
Il volume di un cono si ottiene moltiplicando l’area della
base per la misura dell’altezza e dividendo tale prodotto
per 3.
Se l’apotema del cono è congruente al diametro di base, il cono si dice
equilatero e in esso quindi: a  2r e h  r 3
Quali saranno quindi le formule per il calcolo della superficie laterale, totale e
del volume? Completa tu e ricava quelle inverse.
Sl  r  a  r  2r  .....................
St  .......................  ......................
V  ........................  ......................