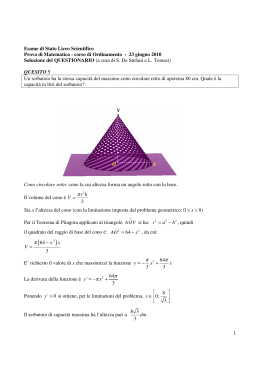
UNIVERSITÀ DEGLI STUDI DI MILANO
DIPARTIMENTO DI MATEMATICA ʺF. ENRIQUESʺ
15
LA SEZIONE DI UN CONO È UNA CONICA ?
COSTRUZIONE
1.
Progetto Lauree Scientifiche
Laboratorio Coniche con Cabri
DEL MODELLO
Sul rettangolo colorato taglia lungo metà curva, seguendo accuratamente l’arco
BCD (per facilitare il lavoro, infila la lama delle forbici nell’incisione).
2.
Taglia lo sviluppo laterale del cono (cui è stata tolta la parte più vicina al
vertice per rendere più facile il montaggio). Taglia accuratamente dal punto A
al punto B e dal punto nero sul bordo destro (dove finisce la tacca sulla linguetta) al
punto D lungo la curva che si trova tra i due archi di circonferenza.
3.
Chiudi il cono, prima sopra e poi sotto il taglio. In ogni caso, sovrapponi il lato
senza linguetta sopra la linguetta corrispondente, in modo che il bordo dove c’è
il punto A sia esattamente sopra la linea che delimita la linguetta e gli estremi delle
linee “orizzontali” combacino; fissa con lo scotch, arrivando con quest’ultimo a un
paio di millimetri dal taglio.
4.
Prova a incastrare tra loro rettangolo e cono: tieni il primo con la parte ruvida
verso l’alto, abbassa leggermente la parte del rettangolo con il punto F2, infila la
punta del cono nel buco e fa’ scivolare la parte tagliata del rettangolo dentro il cono,
in modo che punti segnati con lettere uguali coincidano. Quando hai capito come si
fa, rimuovi con delicatezza l’inserto, metti nel cono la sfera piccola e riposiziona
l’inserto (forse ti sarà più facile se capovolgi il cono...).
5.
Posa la sfera più grande sul tavolo e appoggiaci sopra il cono con l’inserto
colorato. Ora sei pronto per ragionare: infatti, il modello che hai costruito
rappresenta un cono circolare retto tagliato da un piano α avente inclinazione, rispetto
all’asse del cono, maggiore della semiapertura del cono.
QUALCHE
OSSERVAZIONE PRELIMINARE
• Se da un punto P dello spazio tracci due tangenti a una sfera, i segmenti da P ai
punti di tangenza sono tra loro ..............................
• Se da un punto V dello spazio tracci tutte le semirette tangenti a una sfera,
ottieni la superficie di un ......................................................................................
Ogni semiretta si chiama ..................................... del ............... .
I punti di tangenza formano una ....................................... , che appartiene a un
piano ......................................... all’asse del ............... .
• Che cosa cambia se consideri le rette tangenti anziché le semirette?
...............................................................................................................................
UNIVERSITÀ DEGLI STUDI DI MILANO
Progetto Lauree Scientifiche
Laboratorio Coniche con Cabri
DIPARTIMENTO DI MATEMATICA ʺF. ENRIQUESʺ
LA
DIMOSTRAZIONE
• Quante sono le sfere tangenti internamente al cono e tangenti al piano? .......... .
• A quale retta appartengono i centri delle sfere tangenti? .....................................
• Immagina di tagliare cono, piano e sfere tangenti con il piano β passante per
l’asse del cono e per il punto A (e dunque anche per C).
Completa la figura seguente, che rappresenta quello che vedresti sul piano β
(ovvero la sezione con β di cono, piano α e sfere).
G1
G1'
A
F1
C
• Considera i punti G1, G1’ nella figura precedente; a quale linea appartengono i
corrispondenti punti del modello tri-dimensionale? ..........................................
...............................................................................................................................
• Considera il punto F1 nella figura precedente: esso corrisponde al punto di
tangenza ................................................................................................................
• Considera sul modello tri-dimensionale un punto qualsiasi della curva
intersezione della superficie del cono con il piano α, ad esempio quello
indicato con P.
I segmenti PF1 e PP1 sono ................... perché ...................................................
Analogamente, ...... ≅ PP2 , quindi PF1 + ...... ≅ PP1 + PP2 = P1P2.
• Che cosa succede se scegli un altro punto della curva intersezione? Come puoi
concludere che questa curva è un’ellisse? ............................................................
...............................................................................................................................
...............................................................................................................................
...............................................................................................................................
In maniera analoga, si prova che la curva sezione del cono con un piano α è
un’iperbole se α ha inclinazione minore della semiapertura del cono stesso; è una
parabola se l’inclinazione e semiapertura sono uguali (cioè α è parallelo a una
generatrice del cono).