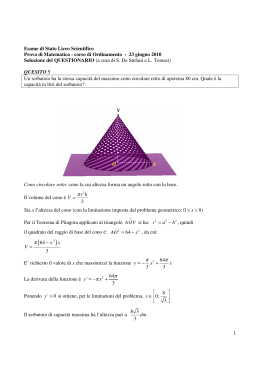
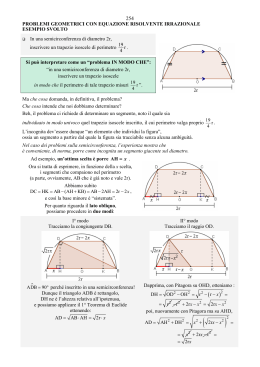
Carlo Sintini, Problemi di maturità, 1972 Luglio, matematicamente.it
Luglio 1972 – Quarto problema
Si determinino l’altezza e il raggio di base del cono di
volume minimo circoscritto ad una sfera di raggio r.
Si dimostri poi che il suddetto cono è anche quello di
minima superficie totale.
OB = OD = r
Risulta
Poniamo AO = x (con x > 0)
AB  r  x
AD  AO2  OD2  x 2  r 2
I due triangoli ADO e ABC sono simili e quindi vale la
proporzione
AD : OD = AB : BC
Da cui si ricava
Carlo Sintini, Problemi di maturità, 1972 Luglio, matematicamente.it
OD  AB r  r  x 

AD
x2  r2
Indicando con y il volume (variabile) del cono, si ottiene
BC 
2
 BC2  AB r  r  x   r  x 
y

3
3  x  r  r  x 
2
(1)
r 2  r  x 
y
3 x  r 
2
Deriviamo per cercare il minimo di questa funzione
2
6r 2  r  x  x  r   3r 2  r  x 
y' 
2
9x  r
y' 
r 2  x 2  2rx  3r 2 
3 x  r 
2
x 2  2rx  3r 2  0
x  r  r 2  3r 2  r  2r 
3r
r
da scartare
Studiando il segno di y’ si ha
Quindi la funzione ha un minimo per x = 3r. Per tale valore
dell’incognita risulta
r  4r
AB  r  3r  4r
BC 
r 2
9r 2  r 2
Il grafico della funzione non è richiesto.
Passiamo ora a calcolare la superficie del cono
St   BC  AC  BC 
Carlo Sintini, Problemi di maturità, 1972 Luglio, matematicamente.it

AC  AB2  BC2 


r r  x

BC 
x2  r2

Sostituendo ed indicando
ottiene
r r  x
y
x2  r2
E, semplificando,
r  x
r2  r  x 
x r  x
 2 2 
x r
x2  r2
2
2
con y la superficie (variabile), si
 x r  x  r r  x  
 2 2 

x2  r2 
 x r
r  r  x 
(2) y 
xr
Questa funzione è uguale alla (1) a meno di una costante e
dunque ammetterà un minimo per lo stesso valore precedente
x = 3r.
2