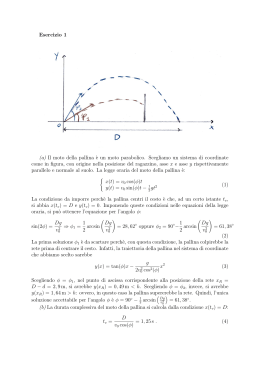
Una pallina di massa m e dimensioni trascurabili può scorrere senza
attrito sulla parete interna di una semisfera di raggio r = 15 cm.
Nell’istante iniziale, la pallina ha una velocità orizzontale e tangente
alla parete e la sua posizione è definita da un angolo θ = 0.60 rad con
l’asse verticale, come indicato in figura. Si determini:
0
O
1. il valore v0 della velocità iniziale per il quale la pallina non varia la
θ
sua quota durante il moto;
2. il momento risultante M, rispetto al centro O della semisfera, delle
forze che agiscono sulla pallina nel corso del moto in funzione
dell’angolo θ;
3. il valore minimo della velocità iniziale vmin necessario perché la pallina arrivi sul bordo
superiore della semisfera.
Soluzione
1) Per rimanere ad una quota costante la componente verticale della risultante delle forze che agiscono sulla pallina
deve essere nulla, per cui, detta R la reazione vincolare, ortogonale alla superficie e quindi diretta verso O, deve
essere
mg = R cosθ
0
La traiettoria sarà un moto circolare uniforme su una circonferenza di raggio rsinθ , e la corrispondente accelerazione
centripeta deve essere fornita dalla reazione vincolare:
0
mv02/(r sinθ ) = R sinθ
0
0
per cui, sostituendo R dalla prima equazione, si ottiene:
v0 = √(rg sin2θ /cosθ ) = 0.75 m/s
0
0
2) La reazione vincolare è sempre diretta verso il polo O ed ha quindi momento nullo. Il momento della forza peso
ha invece modulo
M = rmgsinθ
ed è sempre orizzontale (ed ortogonale al piano individuato dall’asse e dalla posizione della pallina). Nel moto si
conserva quindi la componente verticale del momento angolare della pallina.
3) Si conserva anche l’energia meccanica, per cui, assumendo nulla l’energia potenziale nel punto più basso della
semisfera, possiamo scrivere:
E = ½ m v2 + mgr(1-cosθ) = costante
Nell’istante iniziale, E = ½ m vmin2 + mgr(1-cos θ )
0
2
sul bordo, E = ½ m vb + mgr, da cui
vmin2 = vb2+2grcosθ
0
Il valore minimo richiesto è quello per cui la pallina arriva sul bordo con velocità orizzontale, per cui dalla
conservazione della componente verticale del momento angolare otteniamo:
mvbr = mvminrsinθ
0
e sostituendo vb nella relazione precedente, si ha
v2min (1- sin2θ ) = 2grcosθ
0
0
vmin = √(2rg/cosθ ) = 1.9 m/s
0