Seminario didattico
Ingegneria Elettronica
Lezione 4:
Cinematica e dinamica del punto materiale
1
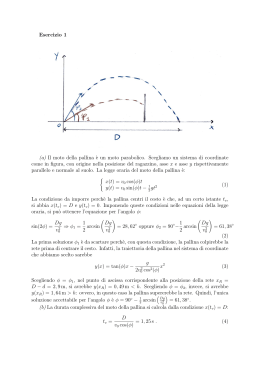
Esercizio 1
Un caccia che vola orizzontalmente alla quota H = 500m con velocità di modulo
v1 = 120 m/s si dirige verso una postazione di difesa contraerea. Quando l'aereo
si trova alla distanza orizzontale D = 4 Km dalla postazione di difesa, viene
sparato un proiettile con velocità iniziale di modulo v0 e con un angolo di tiro α
rispetto all'orizzontale, secondo lo schema mostrato nella figura. Sapendo che
l'aereo viene abbattuto dal proiettile 20 secondi dopo che questo è partito,
calcolare:
1) i valori di v0 e α;
2) in quale posizione l'aereo viene colpito;
3) a quale distanza dalla postazione di difesa precipitano i rottami dell'aereo.
v1
H
v0
α
DATI:
H = 500 m
v1 = 120 m/s
D= 4 km = 4000 m
t1 = 20 s
?v0 e α;
2
D
Esercizio 1
{
Le equazioni del moto dell'aereo del
proiettile sono rispettivamente:
{
1)Nell'istante t1 in cui avviene
l'impatto le coordinate sono
uguali, ovvero xa=xp e ya=yp :
v 20 =
{
1 2
y p t =v 0 sin t g t
2
x p t 1 =x a t 1 v 0 t 1 cos =Dv 1 t 1
1 2
y p t 1 = y a t 1 v 0 t 1 sin g t 1 =H
2
1 2
H g t1
2
tg =
=1,5375 =56,96 °
Dv 1 t 1
Risolvendo il sistema si
ottengono il valore di α e di v0:
2
x a t =Dv 1 t
y a t =H
x p t =v 0 t cos 2
D
H 1
v 1 g t 1 v 0 =
t1
t1 2
2
2
D
H 1
v 1 g t 1 =146,7 m/ s
t1
t1 2
3
Esercizio 1
2)Calcoliamo il punto d'impatto valutando la
posizione dell'aereo a t1:
{
x 1=x a t 1 =Dv 1 t 1 =1600 m
y 1= y a t 1 =H =500 m
3) Dopo l'impatto i rottami dell'aereo cadono dal punto (x1,y1) con velocità v1. Le
equazioni del moto dei rottami, nel sistema di riferimento adottato ,con istante
iniziale quello in cui l'aereo viene colpito, sono le seguenti:
{
x r t =x 1v 1 t=Dv 1 t 1 v 1 t
1 2
1 2
y r t = y 1 g t =H g t
2
2
1 2
2H
Il punto di caduta si trova
y t c =0 H g t c =0 t c =±
imponendo la condizione y = 0:
2
g
Scartando la condizione non
fisica con un tempo negativo,
si ha:
x t c = Dv 1 t 1 v 1 t c =Dv 1 t 1v 1
2H
=387,8 m
g
4
Esercizio 2
Il dispositivo schematizzato in figura è costituito da
un sistema di due dischi D1 e D2, posti ad una
distanza d = 50 cm, che ruotano con velocità
angolare costante ω, intorno allo stesso asse
verticale. Il dispositivo è poggiato su un piano
orizzontale in modo che il disco D1 si trovi ad
un'altezza 2d rispetto al piano. Entrambi i dischi
recano un foro in corrispondenza del bordo,e la
retta che congiunge i due fori A1 e A2 è parallela
all'asse di rotazione. Una pallina viene sparata
verso l'alto da una molla posizionata sul piano
orizzontale in corrispondenza del bordo dei due
dischi, che le imprime una velocità iniziale di
modulo v0. La pallina viene sparata nell'istante in
cui i fori A1 e A2 sono allineati con la molla,
attraversa il foro A1 dopo che i due dischi hanno
compiuto un giro completo, e attraversa il foro A2
dopo che i due dischi hanno compiuto un secondo
giro. Calcolare:
1) la velocità angolare ω dei due dischi;
2) il valore di v0;
3) l'altezza massima raggiunta dalla pallina rispetto
al piano orizzontale.
D2
A2
d
D1
A1
ω
2d
v0
DATI:
d=50 cm
?ω
? v0
? xmax
5
Esercizio 2
L'equazione del moto della pallina:
1 2
x t =v 0 t g t
2
L'equazione del moto dei dischi:
t =t
Sia t1 l'istante in cui la pallina attraversa A1 e t2 quello in cui attraversa A2.
{
1
x t 1 =2d v 0 t 1 g t 21 =2d
2
t 1 =2 t 1=2
{
1 2
x t 2 =2d v 0 t 2 g t 2=3d
2
t 2 =4 t 2=4 Dalle equazioni dei dischi si ricavano i valori di t1 e t2:
2
t 1=
t 2=
4
6
Esercizio 2
Sostituendo i valori dei
tempi nelle equazioni del
moto della pallina si
ottiene:
{
2
2 1 2
=2d v 0 2 g 2 2 =2d 2
g
v0
2 v0
2
4
1 4
=3d v 0 4 g 8 2=3d 2
g
2 Moltiplicando la prima equazione per 2 e combinandole:
{
2
v 0 4 g 4 2 =4d 2 g 4 2=d 2 =± 4 g =±27.82rad / s
d
v 0 4 g 8 2=3d 2
I valori di ω positivi e negativi corrispondono a rotazioni del disco in senso antiorario
o orario, rispettivamente.
Va accettato solo il valore positivo, poiché imponendo θ(t1) =+2π e θ(t2) =+4π si è
implicitamente scelta una rotazione in senso antiorario.
Sostituendo il valore di ω in una delle due equazioni precedenti si ha:
2
2
4
g
g
4
g
5
2
v0 4 g 4 =4d
v0 2
g=4g v 0 = gd=5,534 m/7s
d
d
d
2
Esercizio 2
L'altezza massima raggiunta dalla pallina si trova nel punto in cui si annulla la sua velocità:
{
Equazione del moto e velocità della pallina :
1 2
x t =v 0 t g t
2
v t =v 0g t
v0
v t 3 =v 0 g t 3 =0 t 3 =
g
2
0
2
2
0
1 2 v 1 v0
1 v 25
= d=1,56 m
x max =x t 3 =v 0 t 3 g t 3= =
2
g 2 g
2 g 8
8
Esercizio 3
Un punto materiale si muove lungo una circonferenza di raggio R = 40
cm posta in un piano orizzontale. All'istante t=0 il punto possiede la
velocità v0=2m/s; si osserva che dopo aver compiuto un giro la velocità
vale v1=0.3m/s. La diminuzione di velocità è dovuta ad una forza di
attrito costante. Calcolare il tempo che impiega a fare il giro completo e
l'accelerazione centripeta del punto dopo mezzo giro .
R
v0
DATI:
R=40 cm = 0.4m
v0=2m/s
v1=0.3m/s
at=const
? ac
?t
9
Esercizio 3
Applicando l'equazione per il moto uniformemente decelerato
alla componente tangenziale del moto:
R
v0
2
2
v
v
v 21 v 20=2 s at =4 R at at = 1 0 =0.78m / s2
4
R
Conoscendo l'accelerazione si può calcolare il
tempo impiegato dal punto materiale per
percorrere un giro completo:
v 1v 0
v 1=v 0 at t 1 t 1 =
=2.18 s
at
10
Esercizio 3
Dopo mezzo giro
Applichiamo nuovamente la relazione tra la
velocità l'accelerazione e lo spazio percorso:
O
R
v0
v2
v 22 v 20=2 s at =2
R at v 2 = v 20 2
R at =1.43 m/ s
Poiché l'accelerazione centripeta è legata alla velocità, nel
punto 2 si ha:
v 22
2
an = =5.11 m/ s
R
11
Esercizio 4
Due punti materiali, di masse m1 =8.4 kg e m2 = 10 kg, sono collegati come
in figura, con d1 =0.21 m e d2=0.16 m. Il sistema, che sta in un piano
orizzontale, ruota con velocità angolare costante ω=3 rad/s attorno al
punto 0. Calcolare le tensioni dei fili.
m1
O
d1
m2
d2
ω
DATI:
m1 =8.4 kg
m2 = 10 kg
d1=0.21 m
d2=0.16 m
ω=3 rad/s
? tensioni
12
Esercizio 4
-T1
T1
m1
-T2
T2
m2
ω
O
d1
blocco 1 : T1T2 =m1 a1
blocco 2: T2 =m2 a2
d2
Considerando la
componente radiale:
m1 v 21
blocco 1 :T 1T 2 =
d 1 T 1=m1 2 d 1m2 2 d 1d 2 =49.2 N
2
2
T 2=m2 d 1d 2 =33.3 N
m2 v 2
blocco 2:T 2=
d 1d 2
{
13
Esercizio 5
Tre blocchetti di masse m1= 2 kg, m2 = 3.5 kg, m3 =4.1 kg scendono lungo un
piano inclinato liscio, con angolo θ = 40°, sotto l'azione della forza peso e della
forza F costante. Si sa che la forza tangente al piano a cui è sottoposto il
blocchetto m2 è F2 =8.4 N.
1) Calcolare il valore di F.
2)Si supponga che F non ci sia, ma che il piano presenti attrito, con coefficienti µ1,
µ2=0.84, µ3=0.80 rispettivamente e che il moto sia uniforme.
Calcolare il valore di µ1.
x
m3
m2
F
m1
θ
DATI:
m1= 2 kg
m2 = 3.5 kg
m3 =4.1 kg
θ = 40°
F2=8.4 N.
?F
µ2=0.84
µ3=0.80
a= 0
? µ1
14
Esercizio 5
F2
2
F 2 =m2 a2 a2 = =2.4m / s
m2
Poiché i 3 blocchetti scendono lungo
il piano come se fossero un oggetto
unico, si ha:
a1=a2 =a3 =a
m1m2 m3 g sin F=a m1 m 2m3 F=g sin am1m2 m3 F=37.4 N
15
N3
Esercizio 5
N2
N1
2) Supponiamo F = 0 e il piano non liscio:
m2
m1
θ
Le forze esterne
che agiscono sul
sistema dei 3
blocchi sono:
m3
Fad2
Fad1
P1
P2
Fad3
P3
P1 P2 P3 N 1 N2 N3 Fad1 Fad2 Fad3=0
Per ciascun blocco si ha
lungo la componente
perpendicolare al piano:
N 1P 1 cos =0 m1 g cos =N 1
N 2P 2 cos =0 m2 g cos =N 2
N 3P3 cos =0 m3 g cos =N 3
g sin m1m2 m3 F ad1F ad2 F ad2 =0
g sin m1m2 m3 g cos 1 m12 m23 m3 =0
1
1 =
sin m1m2m3 cos 2 m23 m3 =0.92
m1 cos 16
Esercizio 6
Sopra un piano orizzontale è poggiato un cubo di massa M = 50 kg che può
scorrere senza attrito sul piano. Sopra il cubo è poggiato un altro cubetto di massa
m =10 kg a distanza d= 50 cm dalla faccia AB del cubo piu' grande. All'istante
iniziale, quando tutto è fermo, al cubo è applicata una forza F = 100 N, orizzontale;
dopo t = 2 s il cubetto cade. Calcolare il coefficiente di attrito tra i due cubi.
d
A
F
B
DATI:
M = 50 kg
m =10 kg
d= 50 cm
F= 100 N
t=2s
17
Esercizio 6
N2
d
y
A
N1
Fad
x
Le forze che agiscono
su ciascun blocco sono:
-Fad
P2
B
F
P1
Fad P1 N1 N 2 = M a1
blocco 1 : F
blocco 2: Fad P2 N 2=m a2
Blocco 2:
Blocco 1:
x : P 2N 2 =0 N 2 =mg
y : F ad =ad N 2 =ad m g=m a2 a2 = ad g
x :N 1P 1 N 2=0
Fad mg
y : FF ad =Fad N 2=M a1 a1 =
M
18
Esercizio 6
d
Equazioni del moto dei due blocchi:
y=0
1
2
blocco 1 : y 1= a1 t
1
2
y 1 y 2=d= a1a2 t 2
2
1
2
blocco 2: y 2= a2 t
2
Fad mg
1
2d
2dM
ad g= 2 ad =
F 2 =0.15
M
g Mm
t
t
19
Esercizio 7
A un disco di massa m appoggiato su un tavolo privo di attrito (vedi figura) è
attaccato un filo che passa attraverso un foro al centro del tavolo e tiene appeso
un cilindro di massa M. Trovare a che velocità deve girare il disco su un cerchio di
raggio r per tener fermo il cilindro.
20
Esercizio 7
V N
Disegniamo le forze in gioco e scriviamo le
equazioni dinamiche per i due corpi nelle
componenti radiale e verticale nel caso di
equilibrio:
T
y :T Mg=0
Corpo M
{
rad :T =F centr
Corpo m
y : N Pm =0
T
Pm
PM
Infatti T è proprio uguale
alla forza centripeta del
corpo di massa m:
Mettendo insieme le precedenti relazioni si ricava:
mv 2
T=F centr . =
r
mv 2
= Mg r
Mgr
v=
m
21
Velocità in funzione della posizione nel moto
uniformemente accelerato
Possiamo ottenere un'espressione che non contiene il
tempo sostituendo:
vv 0
v=v 0 a tt 0 tt 0=
a
in:
1
2
x t =x 0 v 0 tt 0 a tt 0 2
Si ottiene:
2
2
0
v =v 2 a xx 0