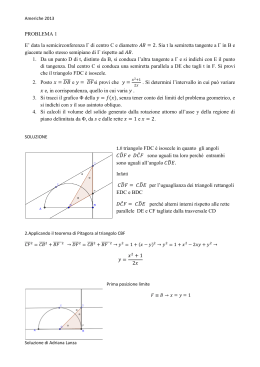
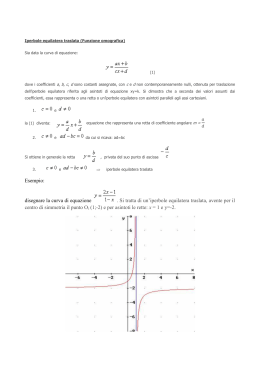
PROBLEMA 1
Data la semicirconferenza di centro O e diametro AB 2r, si prenda su di essa un punto P e si
tracci il raggio OQ parallelo ad AP.
1. Posto
, si calcoli il rapporto:
e lo si esprima in funzione di x 
controllando che risulta:
2. Prescindendo dalla questione geometrica, si studi la funzione f (x) e se ne tracci il grafico .
3. Si scriva l’equazione della retta s che congiunge i punti estremanti relativi di e si verifichi
che essa passa per il punto d’intersezione degli asintoti. Si calcoli inoltre, in gradi e primi
(sessagesimali), l’ampiezza dell’angolo acuto Φ che s forma con l’asintoto obliquo.
4. Si calcoli l’area della regione di piano , delimitata dall’asse x , da e dai suoi asintoti.
Soluzione
1.
AB =2r
=
2. Prescindendo dalla questione geometrica, f(x) è definita per x
La curva incontra l'asse x nei punti
Per studiare il segno di f(x) osserviamo che
f(x) è positiva
<1
incontra l’asse y nel punto D(0;1)
La retta x=-1 è asintoto verticale
Per determinare l’asintoto obliquo calcoliamo
=3
La retta y=-2x+3 è asintoto obliquo
La curva è una conica, essendo una curva algebrica di grado 2 , e precisamente è un’iperbole poiché
possiede due asintoti
Il punto di incontro degli asintoti C(-1;5) è il centro di simmetria.
Studio della derivata
Minimo relativo
f(x) crescente
3.La retta
ha coefficiente angolare
intercetta
La sua equazione è
ed è soddisfatta dalla
coppia ( -1;5), ovvero dalle coordinate del punto C.
Il suo punto di incontro con l’asse x è
Gli asintoti invece incontrano l’asse x nei punti I(-1:0) e
H(
L’angolo
può essere determinato come
differenza tra l’angolo dei due asintoti e l’angolo che la
retta s forma con l’asintoto verticale, ovvero
4-La regione di cui si chiede l’area è la differennza fra il triangolo rettangolo CHI e il trapezoide
relativo a f(x) sull’intervallo
Area del triangolo CHI=
Area del trapezoide
Calcoliamo
+c
area della regione di piano 
–
e