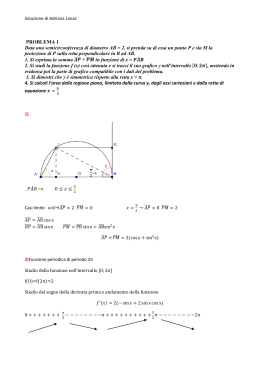
Americhe 2013
PROBLEMA 1
E’ data la semicirconferenza Γ di centro C e diametro
. Sia t la semiretta tangente a Γ in B e
giacente nello stesso semipiano di Γ rispetto ad
.
1. Da un punto D di t, distinto da B, si conduca l’altra tangente a Γ e si indichi con E il punto
di tangenza. Dal centro C si conduca una semiretta parallela a DE che tagli t in F. Si provi
che il triangolo FDC è isoscele.
2. Posto
e
si provi che
. Si determini l’intervallo in cui può variare
e, in corrispondenza, quello in cui varia .
3. Si tracci il grafico Φ della
, senza tener conto dei limiti del problema geometrico, e
si indichi con il suo asintoto obliquo.
4. Si calcoli il volume del solido generato dalla rotazione attorno all’asse y della regione di
piano delimitata da Φ, da e dalle rette
e
.
SOLUZIONE
1.Il triangolo FDC è isoscele in quanto gli angoli
sono uguali tra loro perché entrambi
sono uguali all’angolo
Infatti
per l’uguaglianza dei triangoli rettangoli
EDC e BDC
perché alterni interni rispetto alle rette
parallele DE e CF tagliate dalla trasversale CD
2.Applicando il teorema di Pitagora al triangolo CBF
Prima posizione limite
Soluzione di Adriana Lanza
Americhe 2013
Seconda posizione limite
Intervallo in cui varia x
3.
La funzione
, se non si tiene conto dei limiti geometrici, è definita per
,è
positiva per x>0 e negativa per x<0.
La funzione è dispari, essendo f(-x) = -f(x)
Si tratta di un’iperbole avente il centro di simmetria in O
Poiché
la retta x=0 è asintoto verticale
Scomponendo la frazione nella forma
si osserva che la retta
è asintoto obliquo
Studio della derivata prima
f(x) crescente
f(x) decrescente
I punti (-1;-1) e (1;1) sono rispettivamente massimo e minimo relativo
Essendo un’iperbole non ha flessi- La concavità è verso l’alto per x>0 e verso il basso per x<0, come
conferma lo studio del segno della derivata seconda
Soluzione di Adriana Lanza
Americhe 2013
GRAFICO
4.
il volume richiesto si può calcolare
utilizzando il metodo dei gusci cilindrici
dx=
Soluzione di Adriana Lanza