Quesiti-Liceo della Comunicazione
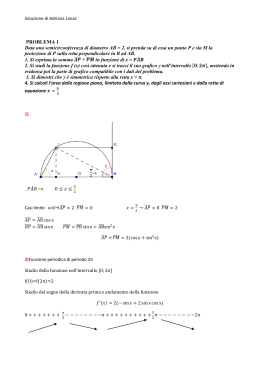
1. Cosa rappresenta il seguente limite e quale ne è il valore?
E’ il limite del rapporto incrementale della funzione f(x)=
con punto iniziale
tendere a 0 dell’incremento h.
( )
Il suo valore , per definizione di derivata, è
Il valore del limite può essere calcolato direttamente, per esempio, sfruttando l’identità
(
)(
(
)
)
=
(
(
Poiché
=1
Il risultato è
=
2.
Si calcoli la derivata diciassettesima di f(x)= cos (x)
E’ facile verificare che
{
Soluzioni di Adriana lanza
)
)
, al
pertanto
3.Si lanciano due dadi. Qual è la probabilità che uno e soltanto uno dei due numeri sia 5?
Risposta
Le uscite possibili sono
I casi favorevoli sono 10
1
2
3
4
5
6
1
2
3
4
*
*
*
*
5
*
*
*
*
6
*
*
Ovvero se A è l’evento {
Indicando con E l’evento {
}
} e con ̅ l’evento {
}
̅
=
4.
Si scriva l’equazione della retta normale al grafico di
Il coefficiente angolare della retta normale è uguale a
Equazione della normale:
5.
Soluzioni di Adriana lanza
nel punto di ascissa
=--
=- 1
Si mostri che, nello sviluppo di
, il coefficiente del termine
è uguale
Nella moltiplicazione
, il monomio
si può ottenere in molti modi, scegliendo k volte il termine a e n-k volte il termine b
Ciò equivale a scrivere una parola di n lettere, di cui k sono uguali ad a n-k sono uguali a b
Per esempio
I possibili anagrammi della suddetta parola sono proprio
6.
E’ noto che il lato del decagono regolare
inscritto in un cerchio è sezione aurea del
raggio. Si utilizzi il risultato per calcolare
Calcolo della sezione aurea del raggio
√
Se il raggio ha misura unitaria, la misura
del lato del decagono è lato ̅̅̅̅del
decagono è
√
√
Soluzioni di Adriana lanza
.
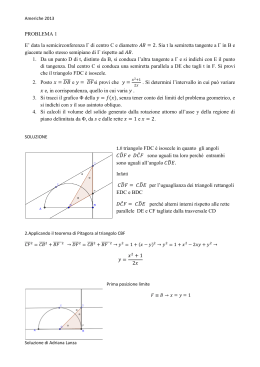
7.E’ dato un tetraedro regolare di spigolo l e altezza h. Si
determini l’ampiezza dell’angolo formato da l e da h.
̅̅̅̅
̅̅̅̅
√
√
8.
Fra le piramidi rette a base quadrata di assegnata superficie laterale S, si determini quella di volume
massimo.
̅̅̅̅
̅̅̅̅
con 0< <a
√
̅̅̅̅
√
=√
=
√
√
√
√
√
(√
V’(x) , nell’intervallo do definizione, si annulla per x=
√
Poiché
√
√
√
) è il valore massimo
Soluzioni di Adriana lanza
e
)
√
√
√
√
√
√
√
9) Il problema di Erone (matematico
alessandrino vissuto probabilmente nella
seconda metà del I secolo d.C.) consiste,
assegnati nel piano due punti A e B, situati dalla
stessa parte rispetto ad una retta r, nel
determinare il cammino minimo che congiunge
A con B toccando r.
Si risolva il problema nel modo che si
preferisce.
Per trovare il percorso più breve ricorriamo a
una costruzione geometrica.
Si costruisce il punto A’ simmetrico di A
rispetto alla retta r.,
. Poiché A’C è congruente ad AC , il problema si riduce a trovare il percorso più breve per andare
da A’ fino a B. In questo caso il percorso più breve è il segmento A’B che incontra in C la retta r.
In figura si può osservare come il cammino ADB è affettivamente maggiore di ACB
La figura dinamica, costruita con Geogebra, permette di effettuare ulteriori verifiche.
Il punto C, così definito, è l'unico punto della retta tale che i segmenti AC e CB formano angoli
uguali con la retta r
Se AC rappresenta un raggio di luce incidente su una superficie piana riflettente, CB sarà il raggio
riflesso
Poiché le rette AC e CB sono simmetriche rispetto alla normale in C alla retta r, si deduce la nota
legge:
L’angolo di incidenza è uguale all’angolo di riflessione.
10)Quale delle seguenti funzioni è positiva per ogni x reale?
Risposta esatta A)
Le funzioni
hanno come immagine l’intervallo [
].
Nei suddetti tre intervalli, l’unica funzione che assume valori solo positivi è il coseno
[ in corrispondenza del quale
L’immagine della funzione
è l’intervallo[
sia la funzione seno che la funzione coseno assumono tutti i valori compresi tra -1 e 1.
Soluzioni di Adriana lanza