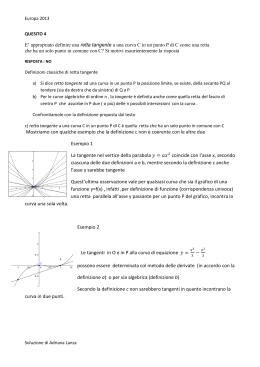
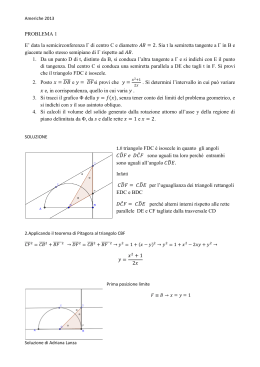
Soluzione di Adriana Lanza
PROBLEMA 1
Data una semicirconferenza di diametro AB = 2, si prenda su di essa un punto P e sia M la
proiezione di P sulla retta perpendicolare in B ad AB.
1. Si esprima la somma
+
in funzione di x =
2. Si studi la funzione f (x) così ottenuta e si tracci il suo grafico γ nell’intervallo
, mettendo in
evidenza poi la parte di grafico compatibile con i dati del problema.
3. Si dimostri che γ è simmetrica rispetto alla retta x = π.
4. Si calcoli l’area della regione piana, limitata dalla curva γ, dagli assi cartesiani e dalla retta di
equazione
1)
.
=x
Casi limite x=0→
co
n
n
n
co
n
2)Funzione periodica di periodo 2π
Stud o della funz one nell’ ntervallo
f
f π
Studio del segno della derivata prima e andamento della funzione
n
n co
Soluzione di Adriana Lanza
Massimi relativi
In e n π
Minimo relativo
hanno altr due m n m relat v per f
Massimo assoluto
Minimo assoluto -2
Studio del segno della derivata seconda e concavitò della curva
co
)=
co
co
co
co
co
co
Sia
co
co
in corrispondenza degli archi evidenziati in
rosso
Concavità verso
0++++++
α-----------------------
l’alto
l ba o
La curva ha fle
n
GRAFICO
πl’alto
π
-------------------- π-α
l ba o
π
l’alto
Soluzione di Adriana Lanza
L’arco d curva evidenziato in rosso rappresenta la parte di grafico compatibile con i limiti
geometrici
3)f π-x) = f(x)
Infatti
4)
co
co
π
n
n
d
π
n
co
n
=