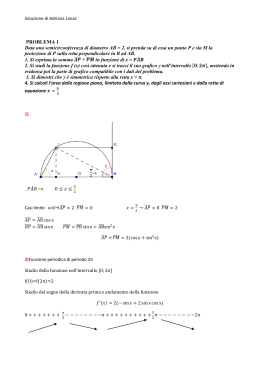
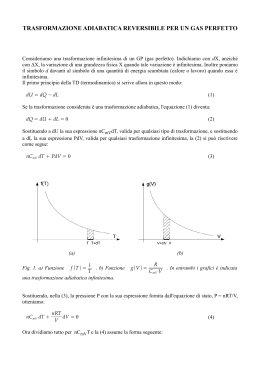
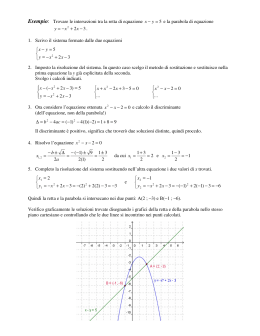
ESEMPI
DI APPLICAZIONI
DELLE
CALCOLATRICI
NELL’INSEGNAMENTO
DELLA MATEMATICA
a cura di Aurelia Orlandoni, Ercole Castagnola,
Sebastiano Cappuccio
2
INDICE
Introduzione pag. ...................................................... 5
Linguaggi algebrici pag. ......................................... 7
Introduzione ai numeri reali pag. ....................... 10
Polinomi pag. ............................................................. 12
Introduzione alle disequazioni pag. ................... 15
Piano cartesiano pag. .............................................. 17
Rette nel piano cartesiano pag. ............................ 19
Equazioni pag. ........................................................... 21
Funzioni pag. .............................................................. 27
Grafici di funzioni e trasformazioni
elementari pag. .......................................................... 30
Problemi e modelli pag. ........................................... 33
Fasci di parabole pag. ............................................. 38
Una proprietà delle cubiche pag. ......................... 41
Due problemi di geometria pag. ........................... 45
Le equazioni di un orsetto pag. ............................ 49
Introduzione alle successioni pag. ........................ 52
Distribuzione delle frequenze pag. ..................... 56
Dalla statistica alla probabilità pag. ................... 60
Regressione e correlazione pag. .......................... 64
Per approfondire pag. ............................................. 71
3
4
INTRODUZIONE
In questo fascicolo sono presentate solo alcune tra le innumerevoli applicazioni in classe possibili con una calcolatrice
grafica e simbolica; in particolare vengono mostrate quelle
nelle quali il rapporto “qualità/ prezzo” (cioè tra l’importanza concettuale e le necessarie conoscenze dello strumento) è particolarmente alto e quindi sono alla portata anche di chi non ha molta esperienza nell’uso delle calcolatrici.
Ciascuna applicazione è preceduta da una “scheda” simile alla seguente:
TITOLO: . . . . . .
ARGOMENTO E CLASSE: . . . . . .
POSSIBILITÀ D’USO: . . . . . .
COMMENTI: . . . . . .
RIFERIMEN- DIFFICOLSTRUMENTO
TO
TÀ
CNG (calcolatrice numerica e
Vengono citati * facilissimo
grafica)
esempi di arti- ** facile
CGS (calcolatrice grafica e simcoli o lavori va- *** medio
bolica)
ri sull’argomen- **** difficile CAS (sistema di elaborazione
to.
Il grado di difsimbolica, sia su computer
ficoltà fa rifeche su calcolatrice)
rimento alle
FE (foglio elettronico)
necessarie co- GD (geometria dinamica)
noscenze dello LP (linguaggio di programmazione, sia su computer che su calstrumento uticolatrice)
lizzato
5
Le indicazioni su “ARGOMENTO E CLASSE” fanno di norma
riferimento alla bozza dei Nuovi Programmi di Matematica
elaborata dalla UMI-CCIM come appare in “Matematica
2003, Attività didattiche e prove di verifica per un nuovo
curricolo di Matematica”.
In molti casi viene riportato come esempio un brano di un
lavoro ritenuto particolarmente significativo. La maggior
parte di questi esempi sono tratti dal CD di ADT 2004, ed.
Ghisetti e Corvi.
NOTA: Molti dei lavori qui pubblicati fanno riferimento
alla calcolatrice TI-92. Le stesse attività possono essere eseguite anche con le equivalenti calcolatrici TI89, TI-89 Titanium e Voyage 200.
6
LINGUAGGI ALGEBRICI
ARGOMENTO E CLASSE
Numeri e algoritmi; uso consapevole delle parentesi.
Primo biennio.
POSSIBILITÀ D’USO
Digitazione di espressioni numeriche (CNG) e letterali (CGS). Traduzione di espressioni numeriche e letterali dal normale “linguaggio algebrico” alla forma lineare e viceversa.
COMMENTI
Un certo addestramento alla digitazione di espressioni (numeriche
o letterali) sulla calcolatrice o al computer (CAS) può essere molto
utile allo studente, non solo come abilità di base per successive applicazioni, ma anche e soprattutto come spunto di riflessione su alcuni importante aspetti dell’algebra di base.
RIFERIMENTO
DIFFICOLTÀ STRUMENTO
/documen/italia/libr *
CNG CGS CAS
o_b/ticap03.pdf
Chiunque operi con una tastiera, sia essa di calcolatrice o di computer, sa bene che non sempre è facile riprodurre espressioni aritmetiche o algebriche perché il tradizionale linguaggio algebrico usa (ad
esempio nelle frazioni o nell’elevamento a potenza) scritture su più
livelli non facilmente riproducibili con la tastiera. Ciò costringe nella
digitazione a operare con un “linguaggio algebrico” almeno in parte
diverso da quello usuale: il formato lineare.
Il formato algebrico lineare
Il dover digitare espressioni in forma lineare costringe a inserire
parentesi anche quando, nel linguaggio algebrico tradizionale, vengono omesse perché non necessarie. Ciò costringe a riflettere sulla
priorità delle operazioni e sull’uso delle parentesi.
Lo studente ha così la possibilità di operare con almeno tre diversi
formalismi algebrici:
x tradizionale
x lineare
7
x grafi ad albero
Il passaggio dall’uno all’altro formalismo consente così una più
approfondita comprensione e una maggiore consapevolezza della
struttura di una espressione. È importante in questo processo di “traduzione” il fatto che i CAS e le calcolatrici grafico-simboliche fanno
rivedere nel formato “tradizionale” ciò che si è scritto, offrendo la
possibilità di controllare la correttezza della digitazione.
Nella tabella che segue vediamo a titolo di esempio alcune espressioni scritte usando la notazione lineare, quella tradizionale e il
corrispondente grafo ad albero:
(5+7)/(42)
/
57
42
+
5
5+7/42
7
5+ 2
4
7
4
+
5
2
–
/
(5+7)/4 – 2
57
2
4
7
4
/
2
+
5
5+7/(4 – 2)
7
5
42
2
4
7
+
5
/
7
4
8
2
L’operazione di elevamento a potenza
Anche l’operazione di elevamento a potenza nel formato tradizionale non può essere riprodotta con una tastiera: è stato così introdotto
un esplicito simbolo (di norma l’accento circonflesso ^) per indicare
questa operazione. Così, ad esempio, 32 deve essere digitato come
3^2. Può sembrare banale, ma il dover utilizzare una struttura del tipo operando – operatore – operando, simile a quella delle altre operazioni, fa sì che lo studente percepisca meglio il concetto di potenza
come operatore e le sue proprietà (o non-proprietà, come la commutativa e la associativa).
I diversi significati del segno “meno”
In ogni tipo di linguaggio non formale (come invece sono ad esempio i linguaggi di programmazione) una parola ha spesso significati assai diversi. Di solito ciò non trae in inganno chi lo usa, perché
egli ne sa interpretare correttamente il significato in base al contesto1; ciò talvolta avviene anche in matematica, ad esempio a proposito della “parola” meno. Una delle principali difficoltà nell’algebra elementare è data dalla gestione del segno “meno”; questo disagio, da
parte di molti studenti, dipende spesso dall’ambiguità di fondo di
questo simbolismo matematico. Lo stesso simbolo viene infatti utilizzato con due diversi significati:
x quello operativo (o di operatore binario) quando indica
l’operazione di sottrazione tra due numeri
x quello predicativo (o di operatore unario) quando indica
l’opposto di un numero.
Nelle calcolatrici sono presenti due diversi tasti per indicare i due
significati del “meno”: - e (-). Ciò non può che chiarire meglio
questa duplice natura del simbolo e costringere così lo studente a
prenderne concretamente coscienza riducendo gli errori di segno che
spesso non sono dovuti a distrazione, ma a una scarsa comprensione
dei significati del simbolo.
1
Ad esempio: “Nella minestra c’è poco sale”, “Le sale del palazzo ospitano
una grande festa”, “Il prezzo del petrolio sale”: la parola sale, pur con significati e ruoli sintattici assai diversi, non crea ambiguità grazie al contesto.
9
INTRODUZIONE AI NUMERI REALI
ARGOMENTO E CLASSE
Numeri reali come numeri decimali. Classe prima:
POSSIBILITÀ D’USO
Individuazione del valore approssimato di numeri reali (ad esempio
radicali quadratici) per tentativi, o, meglio, per approssimazioni
successive.
COMMENTI
Anche questo argomento favorisce la percezione numerica, spesso
distratta dai formalismi algebrici, in particolare nel calcolo con i
radicali.
Nel documento di riferimento viene presentato l’algoritmo delle
“scatole cinesi”.
RIFERIMENTO
DIFFICO STRUMENTO
/documen/italia/labcl LTÀ
CNG CGS CAS
ass/DFOA02.PDF
*
Scatole cinesi (Donata Foà)
Si comincia quasi sempre dalla radice di 2 e si introduce l'algoritmo che permette di approssimarla con la precisione voluta; è abbastanza scomodo ripercorrere questo cammino a mano o con una macchina calcolatrice che dia solo i numeri, è facile perdersi nei numeri
decimali e non vedere bene il procedimento. Proviamo ad usare le liste con il comando seq (sequence).
Visto che ¥2 è compreso fra 1 e 2 si suddivide l'intervallo in dieci
parti con il comando seq che costruisce una sequenza di numeri da
un minimo a un massimo secondo una funzione assegnata, nel nostro
caso 1 + k/10 con k che varia da 0 a 9.
seq(1+k/10,k,0,9) appare la sequenza dei decimali 1.1, 1.2,
1.3 ......se non appare così occorre andare a modificare il tipo di numero da exact a approximate (per fare questo battere il tasto Mode e
andare fino in fondo).
10
Una volta ottenuta la sequenza dei decimali bisogna farne il quadrato per vedere fra quali valori è compreso il 2. Si seleziona la riga
di scrittura, si digita ^2 e si ottengono i quadrati; a mano si sceglie
quello approssimato per difetto e si ricomincia da capo a partire da
questo: l'unica differenza sta nel grado di approssimazione:
seq(1.4+k/100,k,0,9) e così via fino al numero di decimali
voluto.
Per trovare la parte intera di una radice il comando è un po' diverso; supponiamo di avere ¥1398: si può partire da 30 e andare avanti.
seq(k^2,k,30,40) (*il numero limitato di numeri è consigliato
solo per ragioni di schermo*).
È evidente che questo metodo elimina tutta la parte di calcolo e
permette di ricostruire la procedura anche più volte, permette di costruire suddivisioni diverse, in due parti, in tre o in quante si vuole e
quindi individuare la scatola cinese come classe di equivalenza, permette di capire quante operazioni vengono effettuate nelle diverse
partizioni e qual è la più veloce, induce negli studenti l'idea di algoritmo e quindi di costruire un programma che ricalchi questo procedimento.
11
POLINOMI
ARGOMENTO E CLASSE
Polinomi in una indeterminata e, più in generale, calcolo di espressioni letterali. Classe Prima.
POSSIBILITÀ D’USO
Sostituzione di un valore numerico ad una o più variabili di una espressione simbolica.
Tabulazione del valore di una espressione al variare dei valori di
una variabile.
COMMENTI
L’applicazione, di solo apparente banalità, consente di non perdere
la “percezione” numerica del valore di una espressione letterale.
Permette anche di far comprendere come una espressione può assumere valori nulli, positivi, negativi, oppure perdere di significato
a seconda del valore assegnato alla variabile, applicazione propedeutica ai concetti di equazione, disequazione e funzione.
RIFERIMENTO
DIFFICOLTÀ
STRUMENTO
*
CGS CAS FE
Il passaggio dal calcolo numerico a quello simbolico costituisce
una importante tappa nell’apprendimento dell’Algebra. Questo passaggio può essere reso più graduale attraverso l’uso di uno strumento
di calcolo per effettuare la sostituzione di un valore ad una variabile
dell’espressione.
La calcolatrice simbolica, con il tasto with (Ň) e l’ambiente table,
è particolarmente adatta a questo tipo di applicazione. La stessa cosa
può essere realizzata manualmente ma, a causa della pesantezza dei
calcoli, ciò può far perdere di vista questa importante concettualizzazione.
Il tasto with produce una assegnazione locale che sostituisce
nell’espressione indicata a sinistra, il valore indicato a destra della
barra verticale.
12
Fig. 1. Nella prima linea l’espressione viene “semplificata” automaticamente (in questo caso si tratta di una “scomposizione in fratti
semplici”). Nelle linee successive grazie all’uso del tasto with, rappresentato da una barra verticale, l’espressione vene valutata sostituendo alla variabile a rispettivamente i valori 4, 0 e –1.
Fig. 2. Un CAS consente anche sostituzioni “multiple” con più variabili contemporaneamente. Si noti l’uso del connettivo and.
Ciò è molto utile per far sì che lo studente non perda il significato
numerico delle espressioni letterali che deve manipolare e acquisti
una visione “dinamica” di tali espressioni.
La cosa può essere ulteriormente approfondita con l’uso
dell’ambiente Table: dopo aver scritto una espressione simbolica
nell’apposito ambiente di definizione delle funzioni, i valori
dell’espressione possono facilmente essere tabulati facendo variare i
valori della variabile x a partire da un dato valore iniziale con un
“passo” prefissato.
Sarà così facile riconoscere come per determinati valori della variabile l’espressione si annulla, per altri può perdere di significato e
così via (vedi anche scheda successiva).
13
Fig. 3. L’espressione (in questo caso sarebbe ovviamente più corretto
chiamarla funzione, ma a questi livelli scolari probabilmente il concetto di funzione non è ancora stato introdotto) viene definita
nell’apposito Editor.
Fig. 4. Il valore iniziale della tabella tblstart x = 0 e il passo 'tbl = 1
sono i valori di default. Possono comunque essere modificati in qualsiasi istante dall’utente.
Fig. 5: Nell’ambiente Table vengono tabulati i valori della funzione
(anzi, nel nostro lessico in questo contesto, della espressione) data:
nella prima colonna compaiono i valori della variabile x, nella seconda colonna i valori dell’espressione corrispondenti ad essi.
14
INTRODUZIONE ALLE DISEQUAZIONI
ARGOMENTO E CLASSE
Equazioni e disequazioni di primo grado a una incognita.
Primo biennio.
POSSIBILITÀ D’USO
Tabulazione di una funzione con l’ambiente Table.
COMMENTI
Anche un CAS (ad esempio Derive con l’uso di Vector) o un foglio
elettronico permettono la stessa cosa, ma in modo meno espressivo
e immediato e soprattutto più complesso da realizzare.
RIFERIMENDIFFICOLTÀ
STRUMENTO
TO
* con le calcolatrici grafiche CG
e/o simboliche
CGS
** con un altro CAS
CAS
** con il foglio elettronico
FE
Per questo argomento la tecnologia facilita un importante salto
concettuale: quello dalle equazioni alle disequazioni.
Spesso, paradossalmente, l’aver appreso le tecniche di calcolo
delle equazioni può costituire un ostacolo all’apprendimento delle disequazioni: non dobbiamo scandalizzarci se uno studente, che viene
lodato se scrive x = r3 come risultato dell’equazione x2 = 9 , si stupisce di essere rimproverato quando scrive x > r3 come risultato della
disequazione x2 > 9: il suo disorientamento è comprensibile!
Si propone quindi di calcolare il valore di una espressione in una
data variabile (che potremmo chiamare ad esempio x) al variare di tale x. Non è neppure necessario aver già introdotto il concetto di funzione, anzi, tutto ciò può anche essere propedeutico a tale argomento.
Viene poi posto il problema di studiare il segno di una “espressione”, inteso come individuazione dei valori della variabile che
danno origine a un valore positivo, negativo, nullo o che non possono generare alcun valore. Gli aspetti relazionali e funzionali di tale
argomento potranno poi essere approfonditi in un secondo momento.
x2
Vediamo ad esempio l’espressione:
x5
15
Lo studente potrà così vedere come il valore assunto dall’espressione
si modifica al mutare del valore assegnato alla variabile: la calcolatrice gli offre un modello dinamico che sostituisce la visione “statica” usata fino ad allora in Algebra.
Saranno poi possibili “esplorazioni” dirette scorrendo la tabella
dei valori o modificando il passo di variazione della variabile.
Da queste esplorazioni sorgeranno poi spontaneamente i limiti di
tale modo di agire: ad esempio la difficoltà che talora si presenta
nell’individuare gli zeri (si pensi alla tabulazione dell’espressione
5x21 nella prima figura sotto) o i valori in corrispondenza dei quali
l’espressione (7x – 8)/(6x – 7) (nella seconda figura sotto) assume
valori negativi. In questo esempio sarà necessario adottare una “rete
a maglie più strette” per individuare la presenza dell’intervallo desiderato, mentre nel precedente, a causa della natura degli zeri, la nostra “rete a maglie necessariamente razionali” riesce a “circoscriverli” ma non a individuarli.
Si presenta così la necessità di un procedimento esatto che permetterà di studiare il segno di una espressione e si potranno quindi
introdurre il concetto di disequazione e le relative tecniche di calcolo
per la ricerca degli eventuali valori della variabile che forniscono un
risultato, ad esempio, positivo.
16
PIANO CARTESIANO
ARGOMENTO E CLASSE
Il piano cartesiano: il metodo delle coordinate. Classe Seconda,
Terza.
POSSIBILITÀ D’USO
Costruzione di una libreria di funzioni e loro uso nella risoluzione
di problemi. Ad esempio: DIST(xa,ya,xb,yb), per calcolare la distanza tra due punti, PMED(xa,ya,xb,yb) per determinare le coordinate del punto medio di un segmento…..
COMMENTI
In questo caso si propone la costruzione di una libreria di funzioni
nell’ambito della geometria analitica, ma se ne potrebbero realizzare altre, ad esempio in trigonometria relativamente alla risoluzione
dei triangoli, o in analisi per la determinazione delle rette tangente
e normale al grafico di una funzione ecc.
RIFERIMENTO
DIFFICOLTÀ
STRUMENTO
V. scheda successiva **
CGS CAS
Non scenderemo in dettaglio in questa sede, rimandando alla lunga lista di riferimenti elencato nella scheda successiva.
Ci limiteremo a far osservare che le funzioni qui proposte sono
estremamente semplici, tanto da non richiedere l’uso del linguaggio
di programmazione, ma una semplice assegnazione con il tasto STO
nell’ambiente di calcolo.
Ad esempio per definire la funzione DIST basterà digitare:
—((xa-xb)^2+(ya-yb)^2) STO DIST(xa,ya,xb,yb)
Il principio ispiratore di questo tipo di attività è concentrare
l’attenzione dello studente sul metodo risolutivo del problema proposto utilizzando gli strumenti che ha a disposizione. Particolarmente
significativo è il ruolo dello studente che non si limita ad applicare
formule precostituite (questo lavoro è demandato alla macchina) ma
si fa attore del proprio apprendimento e costruttore del proprio sapere. Interessante è anche la fase di verifica della correttezza delle
“formule” implementate nella libreria, fase che viene demandata allo
17
studente, la ricerca e il riconoscimento di “situazioni estreme” e
l’interpretazione dei risultati forniti dalla macchina in questi casi.
Ecco alcuni esempi di problemi:
x riconoscimento dell’allineamento di tre punti A, B, C se AC
= AB+BC (e B compreso fra A e C),
x riconoscimento di triangoli rettangoli, dati i vertici, se i lati
verificano la relazione pitagorica,
x riconoscimento di quadrilateri particolari (ad es. parallelogrammi, rombi, rettangoli) dati i vertici e usando le note proprietà (ad es. diagonali con il medesimo punto medio),
Da non trascurare anche la possibilità di dare compiti con dati tutti diversi tra uno studente e l’altro: poiché le difficoltà di calcolo perdono drasticamente di importanza, non esistono più calcoli “facili” o
“difficili” né risultati “belli” o “brutti”: l’unica cosa importante è la
correttezza del metodo risolutivo.
Si noti infine anche la possibilità di definire le funzioni fornendo
come argomenti delle funzioni le coordinate dei punti interessati
(come qui sopra suggerito) oppure di utilizzare, se lo si desidera,
strutture di dati più complesse come le liste o i vettori, individuando
così i punti attraverso un loro identificatore.
18
RETTE NEL PIANO CARTESIANO
ARGOMENTO E CLASSE
Il piano cartesiano: il metodo delle coordinate. Classe Terza
POSSIBILITÀ D’USO
Prosegue la costruzione della libreria di funzioni e loro uso nella risoluzione di problemi.
COMMENTI
Ancora una volta la “libreria” di funzioni sarà usata come
“cassetta degli attrezzi” per la risoluzione di problemi di
maggiore complessità. La creazione e l’uso sistematico di una
libreria di funzioni, oltre ad essere di per sé un utile esercizio,
stimola l’abitudine alla generalizzazione, favorisce la divisione di problemi in sottoproblemi, consente di risolvere con pochissimi calcoli manuali e in breve tempo problemi anche di
notevole complessità, ponendo l’accento soprattutto sul metodo risolutivo.
RIFERIMENTO
/documen/italia/labclass/
GRAVE02.PDF
/documen/italia/labclass/
MCHIM01.PDF
/documen/italia/labclass/
NNOLL02.PDF
DIFFICOLTÀ
**
STRUMENTO
CGS CAS
Alcuni esempi:
RETTA(xa,ya,xb,yb) per determinare l’equazione della retta passante per due punti. DPR(xa,ya,a,b,c) per calcolare la distanza tra un
punto e una retta
PARALL(punto, retta) per determinare l’equazione della retta passante per un punto dato e parallela a una retta data
PERPEN(punto, retta) per determinare l’equazione della retta passante per un punto dato e perpendicolare a una retta data
.…..
19
Si noti che queste implementazioni delle formule di geometria
analitica possono essere utilizzate a loro volta come “macro” per costruirne delle nuove.
Ad esempio potrà essere così definita la funzione che, date le coordinate di due punti, determina l’equazione dell’asse del segmento
di cui essi sono estremi come luogo di punti equidistanti dagli estremi stessi:
solve(DIST(xa,ya,x,y)=DIST(xb,yb,x,y),y) STO
ASSE(xa,ya,xb,yb)
Vale quanto già detto nella scheda precedente riguardo al riconoscimento di “situazioni estreme” e all’interpretazione dei risultati
forniti dalla macchina. Ad esempio, nel caso in cui la retta sia parallela all’asse delle ordinate, la nota formula che viene applicata in
RETTA(xa,ya,xb,yb) è ovviamente inefficace; ma in tali casi lo studente potrà (anzi, dovrà) riconoscere la situazione, saper motivare il
mancato funzionamento del suo “attrezzo” e arrivare manualmente al
risultato desiderato.
Si noti che queste funzioni sono definite direttamente
nell’ambiente Home senza passare attraverso l’ambiente di programmazione e che, fatto non irrilevante, per definirle sono state usate altre funzioni definite in precedenza: la costruzione di “attrezzi”
più semplici ci permette la costruzione di “attrezzi” via via sempre
più complessi.
Se si desidera dare un maggiore risalto agli aspetti algoritmici, utilizzando il linguaggio di programmazione e le strutture di controllo
in esso disponibili, possono essere definite funzioni più sofisticate,
che tengano conto delle varie situazioni particolari che possono presentarsi. Nei documenti in riferimento vengono presentate librerie di
questo tipo.
20
EQUAZIONI
ARGOMENTO E CLASSE
Equazioni e sistemi di equazioni. Primo Biennio – Secondo Biennio
POSSIBILITÀ D’USO
Risoluzione di equazioni e sistemi.
COMMENTI
Viene qui di seguito riportato un documento elaborato, come altri
presenti in questo fascicolo, nell’ambito del progetto Labclass. Si
tratta di uno sguardo di assieme sulle possibilità offerta dalle
calcolatrici simboliche nella risoluzione di equazioni.
RIFERIMENTO
DIFFICOLTÀ STRUMENTO
/documen/italia/labclass/ **
CGS CAS
dfoa02.PDF
Il comando Solve (Donata Foà)
Questo è il comando più importante perché permette di risolvere
equazioni, disequazioni di primo grado, in maniera esatta o approssimata secondo le situazioni.
La sintassi è la seguente:
solve(equazione/disequazione,variabile)
E’ necessario indicare rispetto a quale variabile si vuol risolvere.
Questo è un passaggio fondamentale per gli studenti che si abituano a considerare le variabili tutte come potenziali incognite, senza
privilegi impliciti:
Digitare
solve(a*x=b,x) solve(a*x=b,a) solve(a*x=b,b)
La macchina non sa fare la discussione delle equazioni e non pone vincoli, si limita a dire se l'uguaglianza è vera o falsa quando i
vincoli li mettiamo noi. Per esempio solve(a*x=b,x) dà come
risultato b/a a meno che non si ponga noi la condizione a = 0.
21
In questo caso occorre utilizzare il comando with ([2nd] k) e scrivere solve(a*x=b,x)| a=0 e il risultato è "false" 2.
Nel caso però di equazioni numeriche in cui la soluzione non sia
accettabile come ad esempio
x 1
4
dà la risposta "false" e di fronte a un'identità risponde
x3 x3
"true"
Una cosa interessante e istruttiva per gli studenti, nella soluzione
di equazioni, come anche in altri contesti, è la possibilità di far lavorare la macchina passo passo, indicandole i passaggi uno ad uno senza usare il comando solve ma usando i principi di equivalenza delle
equazioni.
Si voglia risolvere
3x - 2 = 5 - 4x.
Si seleziona la riga di scrittura e si digita +4x; la scritta diventa
ans(1)+4x; ciò significa che si è sommato ad entrambi i membri
4x e nello schermo compare 7x - 2 = 5; sempre selezionando la riga
di scrittura si digita +2; diventa 7x = 7; si digita /7 e appare x = 1.
2
Sulla voyage 200, sulla TI-92 Plus e sulla TI89 compare “0=b” e non “false” [N.d.R. ]
22
Questo procedimento (operare con la stessa operazione in entrambi i membri di un'equazione) si può applicare sempre purché si
sia disposti a fare o a far fare alla macchina il controllo dei risultati;
Si voglia risolvere —(x2+1) = x - 1.
Selezionando la riga di scrittura si digita ^2 e si ottiene il quadrato di
entrambi i membri:
(x^2+1) = (x-1)^2
se non si attiva nessun controllo la soluzione che si ottiene x = 0 è
falsa ma è una buona occasione per discuterne con gli studenti e porre la condizione che x sia maggiore di 1 con il comando with; la risposta diventa false.
Di fronte a equazioni con più soluzioni, queste appaiono separate
dal connettivo or .
Ad esempio provate a risolvere l'equazione 2x = x2 oppure l'equazione x2 - 2x+5 = 0 oppure 2x2 - 4x - 3 = 0.
Quanto alle disequazioni, con la stessa procedura delle equazioni
si riesce a risolvere quelle di primo grado, non quelle di grado superiore.
Equazioni trigonometriche, in cui le soluzioni sono infinite, del
tipo:
2sin(x)cos(x) - sin(x) = 0
vengono risolte col comando solve e le soluzioni appaiono come in
figura (@n1 è l'equivalente di k numero intero)
Alcune applicazioni effettuate nel lavoro curricolare:
1) Risoluzione di sistemi
­3x 2 y 1
.
Si voglia risolvere il sistema ®
¯5 x y 3
23
Si possono seguire le stesse strade che si percorrono manualmente
senza fare errori di calcolo e essendo costretti a evidenziare le operazioni e quindi il processo logico;
solve(5x+y=3,y): appare la funzione nella forma y = f(x).
solve( 3x-2y=1| y=-5x+3,x): appare la soluzione in x.
Il comando | (with) significa "con la condizione assegnata" ovvero
con la y uguale a quella espressa nell’uguaglianza precedente; il dover specificare rispetto a quale variabile si risolve è importante e significativo.
Altrimenti si può operare col metodo di riduzione moltiplicando
opportunamente le due equazioni e sommandole fra loro:
selezionare l’espressione 5x + y = 3, moltiplicarla per 2: si ottiene un'equazione in cui le y hanno lo stesso coefficiente; occorre sviluppare l'espressione con il comando Expand; selezionando quest'ultima
espressione e digitando ans(1)+(3x-2y=1) si ottiene la somma
membro a membro in cui è scomparsa la y; non resta che dividere il
risultato per 13 per ottenere la soluzione in x; per la y basta utilizzare
il comando solve e risolvere una qualsiasi delle due equazioni con la
condizione che x = 7/13 rispetto alla y.
Per studenti un po' più grandi che hanno già sentito parlare di trasformazioni, di vettori e matrici si possono appunto usare le matrici:
digitare [3,-2;5,1] sto matrice (*la matrice del sistema*)
[1;3] sto vett (*il vettore dei termini noti*)
simult(matrice,vett): restituisce il risultato del sistema
sotto forma di vettore [7/13; 4/13].
La virgola sposta l'elemento nella stessa riga, il punto e virgola
cambia riga.
24
Anche senza assegnare la matrice o il vettore a delle variabili si può
procedere per esteso:
simult([3,-2;5,1],[1;3]):
Nella riga sopra compaiono scritte esplicitamente la matrice e il vettore (sulla sinistra) e il risultato (sulla destra).
Quando si ha a che fare con una parabola passante per tre punti
questa è,probabilmente, la via più conveniente.
Niente vieta comunque di usare il metodo di riduzione anche in
questo caso: certo è un po' più complicato, ma diventa accessibile se
si usa il comando ans(n) ovvero "answer n" che richiama il risultato che sta n passi avanti: ans(1) è il risultato immediatamente precedente, ans(2) quello subito sopra e così via.
Proviamo su questo caso:
­x y z 2
°
®2 x 3 y 4 z 0 .
° x 2 y 2 z 3
¯
ans(1)+ans(3) restituisce un'equazione nelle sole y e z, che ora
è diventata ans(1), quindi 2*ans(4)-ans(3) dà un'equazione
in y e z.
25
È chiaro che si può procedere così fino alla fine ed è anche chiaro
che si deve esprimere a parole con chiarezza cosa si vuol fare, quale
equazione si vuol modificare e perché.
Non è poca cosa da pretendere dagli studenti.
Se il sistema da risolvere non è di primo grado il procedimento è
lo stesso; provare l'intersezione di un cerchio con una parabola opportuna; vengono espresse anche le condizioni di realtà delle radici.
26
FUNZIONI
ARGOMENTO E CLASSE
Funzioni. Secondo Biennio
POSSIBILITÀ D’USO
Definizione e uso di funzioni.
COMMENTI
Una funzione può essere rappresentata secondo vari “registri rappresentativi”, ad esempio quello proposizionale, quello algebrico,
quello grafico-cartesiano, quello tabulare e infine come “macchina”
che, ricevuto un input, produce un output. È importante che
l’alunno impari a utilizzare correttamente tutti questi registri e che
sappia passare con disinvoltura dall’uno all’altro.
RIFERIMENTO
DIFFICOLTÀ
STRUMENTO
/documen/italia/altro/pa * con le calcolatrici CG
cco13.PPT
simboliche
CGS
/documen/italia/labclass/ ** con un altro CAS CAS
gserv01.pdf
** con il foglio elet- FE
/documen/italia/labclass/
tronico
gserv02.pdf
Tra gli strumenti proposti la calcolatrice simbolica appare lo
strumento più adatto, vista la facilità di utilizzare una stessa funzione
nei vari registri e di passare dall’uno all’altro con la semplice pressione di un tasto: una funzione (o anche più di una contemporaneamente) può essere definita nell’ambiente di calcolo Home con una
semplice assegnazione, oppure nell’apposito ambiente Y=Editor.
Fig. 1. La definizione di una
funzione nell’ambiente
Y=Editor.
Fig. 2. La tabulazione automatica dei valori della funzione
nell’ambiente Table (a sinistra) e
27
il grafico nell’ambiente Graph
della funzione prima definita. Si
noti la possibilità di suddividere
lo schermo in due parti.
Fig. 3. Le stesse operazioni (definizione di una funzione, sua tabulazione e grafico) possono essere facilmente realizzate anche con
una semplice calcolatrice grafica di basso prezzo, sacrificando solo
qualcosa nella risoluzione dello schermo grafico. Si noti (seconda
immagine) che anche con queste calcolatrici è possibile modificare
il valore iniziale e il passo di tabulazione.
Fig. 3. Altri due modi di definire una funzione nell’ambiente di calcolo Home di una calcolatrice simbolica.
I valori della funzione possono essere poi tabulati nell’ambiente
Table ed è immediato ottenere una rappresentazione grafica
nell’ambiente Graph.
Infine se la calcolatrice ha anche la possibilità di eseguire calcoli
simbolici, le funzioni definite possono essere manipolate tornando
nell’ambiente di calcolo Home.
28
Fig. 4. Le funzioni y1(x) e y2(x) Fig. 5. Di norma la composiziosono l’una l’inversa dell’altra
ne di due funzioni non è commupoiché la loro composizione è la tativa.
funzione identica.
Questa ricchezza di modelli e di ambienti facilita la comprensione
del concetto di funzione. Attività simili (escluse ovviamente le manipolazioni simboliche) possono essere realizzate anche con un foglio
elettronico; questo strumento però presenta maggiori difficoltà d’uso
perché i comandi da impartire e i menu da attivare sono più complessi, tanto da rischiare di far perdere di vista l’obiettivo principale, che
è quello della creazione, analisi e manipolazione di funzioni.
29
GRAFICI DI FUNZONI E
TRASFORMAZIONI ELEMENTARI
ARGOMENTO E CLASSE
Rappresentazione analitica di trasformazioni geometriche elementari (traslazioni, rotazioni con centro nell’origine, simmetrie, omotetie, dilatazioni). Secondo Biennio
POSSIBILITÀ D’USO
Una possibilità è mostrare grafici di funzioni sottoposte a trasformazioni elementari: l’insegnante mostra come viene modificato il
grafico in relazione ad una trasformazione effettuata sulla sua equazione.
COMMENTI
Possono essere messe a frutto le possibilità grafiche di CAS e calcolatrici. L’insegnante può utilizzare qualche strumento di visualizzazione collettiva (videoproiettore, viewscreen…) per mostrare
agli alunni ciò che appare sullo schermo della sua calcolatrice, oppure può predisporre schede di lavoro per guidare il loro lavoro.
Possono essere sottoposti agli alunni esercizi del tipo:
x costruire una funzione a partire da una funzione già nota il
cui grafico risponda a certe caratteristiche.
x visualizzare sullo schermo della calcolatrice o del computer il grafico di una funzione che, a causa di opportune trasformazioni (traslazioni, dilatazioni ecc.), non appare nello
schemo con scala standard.
RIFERIMENTO
DIFFICOLTÀ
STRUMENTO
/documen/italia/labclass/ * con le calcolatrici CG
ntamb03.PDF
grafiche e con CGS
/documen/italia/labclass/
quelle simboliche
cmocc06.PDF
** con un altro CAS CAS
/documen/italia/montesil ** con il foglio elet- FE
v/distefan.PDF
tronico
30
Grafici di funzioni: il gioco dello Slalom
Un argomento, oggigiorno abbastanza “di moda” nell’insegnamento, è quello dei grafici di funzioni sottoposte a trasformazioni
elementari: dato il grafico di una funzione f(x), quello di f(x) + k si
ottiene da questo con una traslazione verticale, quello di f(x + k) con
una traslazione orizzontale (verso destra se è k < 0, verso sinistra se è
k > 0); così k f(x) ha un grafico che si ottiene da quello di f(x) con
una “dilatazione” in direzione verticale, quello di f(x/k) una “dilatazione” in direzione orizzontale (ovviamente con k > 1) e così via.
La cosa ha una notevole importanza per una “percezione” geometrica del grafico delle funzioni e ovviamente l’uso di uno strumento
come una calcolatrice grafica può aiutare molto lo studente. Ma
l’argomento si presta bene anche ad un gioco: quello dello slalom.
Viene dato un insieme di “birilli” (vedi Fig. 1), ad esempio i punti
di coordinate (1; 3), (3; 3), (5; 3), (7; 3) e lo studente viene invitato a
trovare una funzione trigonometrica che “faccia lo slalom tra i birilli”
cioè il cui grafico passi tra i punti lasciandoli alternativamente uno a
destra e il successivo a sinistra o viceversa. In altre parole lo studente
viene invitato a costruire un grafico simile a quello mostrato in Fig.
2.
Fig. 1.I birilli del gioco dello
Slalom e il grafico della
funzione di partenza sinx.
Fig. 2 Una possibile soluzione
del gioco.
Una recente ricerca (Trouche, 1997) ha individuato diverse tipologie di comportamento nell’uso della calcolatrice da parte dello studente, ciascuna con i suoi pregi e i suoi difetti. Per ottenere un ragionevole compromesso tra il comportamento “razionale” e quello “sperimentale” e “bricoleur”, propongo il gioco sotto forma di scheda di
31
lavoro per conservare traccia delle trasformazioni effettuate e per costringere gli alunni ad un lavoro consapevole e non casuale: un rischio infatti è quello dell’andare a casaccio, favorito questo dalla velocità con la quale la calcolatrice permette di tracciare il grafico.
Una possibile variazione sul tema è chiedere un analogo slalom
però questa volta effettuato con una funzione polinomiale.
Il problema non è difficile ma neppure banale: una possibile strategia potrà essere quella di cercare una funzione polinomiale che abbia come zeri, ad esempio, 0, 2, 4, 6, 8, modificarla in modo da
“comprimerne” il grafico in direzione verticale e infine traslarla verso l’alto perché le sue evoluzioni tra i “birilli” siano quelle desiderate.
32
PROBLEMI E MODELLI
ARGOMENTO E CLASSE
Scegliere, adattare, costruire, utilizzare schematizzazioni matematiche di situazioni e fenomeni matematici e non per risolvere problemi. Primo Biennio
POSSIBILITÀ D’USO
Le capacità di visualizzazione e di modellizzazione offerte da strumenti come i CAS e le calcolatrici grafiche possono essere messi a
frutto in modo particolarmente significativo nella modellizzazione
e nella risoluzione di problemi.
COMMENTI
Viene qui presentato come esempio un lavoro svolto da una Collega nell’ambito di una sperimentazione sull’uso delle calcolatrici
promossa dall’IRRE Emilia/Romagna durante l’Anno Scolastico
2000/2001.
RIFERIMENTO
DIFFICOLTÀ
STRUMENTO
http://www.fardiconto.it/ ** con le calcolatrici CG CGS CAS
calcolatrici/TI89/index.
o altro CAS
htm
Disequazioni di primo grado e problemi di scelta (M. Cavicchi)
PRIMA FASE
…… omissis ……
SECONDA FASE
Con gli strumenti forniti agli studenti la lezione precedente ho fatto impostare e risolvere graficamente i seguenti problemi tratti dal testo “Multi_Format” Maraschini- Palma:
1.
Il prezzo richiesto da una azienda di trasporti per consegnare un
voluminoso armadio è di 13 € più 2 € per il numero dei piani in
cui si trova l’appartamento del cliente; scrivi e rappresenta graficamente la funzione che esprime la spesa sostenuta per il trasporto in funzione del numero di piani;
33
2.
Una sarta che lavora in casa guadagna nell’arco di un mese 60 €
fissi più 4,50 € per ogni pezzo cucito; esprimi la funzione che
rappresenta il guadagno della sarta, rappresenta la graficamente
ed utilizzando la calcolatrice rispondi alla domanda: se in mese
ha guadagnato 600 €, quanti pezzi ha cucito in quel mese?
3.
Un rappresentante di piccoli aspirapolvere in un mese guadagna
300 € fissi più una provvigione del 15% su ogni pezzo venduto,
il cui costo per gli acquirenti è di 55 €; imposta la funzione che
esprime il guadagno e rispondi: quanto ha guadagnato in un mese se il suo incasso è stato di 1815 €?
34
4.
Un commerciante guadagna in media 15 € per ogni articolo venduto meno 500 € di spese fisse al mese; imposta la funzione del
guadagno e rispondi: quanti articoli deve vendere mensilmente
per non essere in perdita?
5.
Un camper può essere affittato da una ditta A con le seguenti
modalità: una quota fissa di 120 €; una giornaliera di 45 €; può
essere invece affittato da una ditta B pagando una quota fissa di
25 € ed una quota settimanale di 350 €. Rappresenta graficamente le due situazioni e stabilisci quale delle due è più conveniente
se si vuole affittare il camper per due settimane.
35
Quest’ultimo problema mi ha dato lo spunto per passare alla terza fase:
TERZA FASE
Abbiamo rappresentato due funzioni nel piano cartesiano ed abbiamo determinato la soluzione grafica del sistema lineare dato dalle
due equazioni;
QUARTA FASE
Abbiamo poi confrontato le ordinate delle due funzioni
nell’ambiente Table, osservando l’alternativa più conveniente anche
dal punto di vista delle ordinate delle due funzioni.
QUINTA FASE
PROVA DI VERIFICA SVOLTA CON L’AUSILIO DELLA
CALCOLATRICE GRAFICO-SIMBOLICA TI89
1.
Ambiente Y=EDITOR:
Definisci in y1(x) e y2(x) le funzioni che traducono il seguente
problema di trasporto:
per la spedizione di alcuni quantitativi di merce possono essere utilizzate due forme di trasporto. Il costo di ognuna si compone di una
quota fissa ed una quota per ogni unità di merce ed è espressa dalle
funzioni:
A: y = 10x+500
B: y = 8x+1200
2. Ambiente GRAPH :
Traccia il diagramma cartesiano delle due funzioni e determina
l’eventuale intersezione, evidenziandola con opportuni zoom ; riporta
il grafico nello spazio sottostante.
36
3.
Risolvi il seguente problema:
Si chiede di determinare quale sia l’alternativa di costo minore al
variare delle quantità x della merce da trasportare.
Suggerimento: utilizza oltre al grafico anche l’ambiente TABLE dal
quale puoi avere la tabella dei valori delle due rette.
OSSERVAZIONI SULLA SPERIMENTAZIONE IN CLASSE
L’uso della calcolatrice TI-89 ha sicuramente interessato i ragazzi
che hanno risposto molto positivamente al test sul gradimento loro
somministrato sollecitandone l’utilizzo sistematico in classe anche
per gli altri argomenti del programma. I vantaggi che ne ho tratti
sull’insegnamento della materia sono stati molteplici:
x I ragazzi più motivati hanno potuto utilizzare lo strumento
per approfondire i concetti nuovi;
x Gli allievi si sono appassionati all’uso dello strumento ed
hanno “fatto” loro stessi delle prove autonome per individuare delle proprietà;
x Anche i meno motivati attratti dalla novità hanno lavorato in
classe con interesse.
Ritengo però che sia stato un limite il poter utilizzare per così
breve tempo le calcolatrici e soprattutto il non avere dato la possibilità ai ragazzi di portarla a casa e quindi di utilizzarla autonomamente
anche nel lavoro domestico.
37
FASCI DI PARABOLE
ARGOMENTO E CLASSE
Coniche. Secondo Biennio.
POSSIBILITÀ D’USO
Costruzione di coniche come luoghi geometrici.
Supporto algebrico nella risoluzione di esercizi.
Creazione e rappresentazione grafica di “fasci” di coniche ed esplorazione delle loro proprietà.
COMMENTI
Con pochi facili comandi è possibile creare insiemi di equazioni di
coniche facendo variare uno dei coefficienti da un valore minimo a
uno massimo a un determinato passo.
I “fasci” così ottenuti si prestano a interessanti esplorazioni, alla
formulazione di congetture, alla scoperta di proprietà.
Attraverso la visualizzazione grafica acquista concretezza la distinzione tra variabile e parametro e l’influenza di ciascuno dei coefficienti dell’equazione di una conica sulle caratteristiche del suo grafico. Purtroppo, contrariamente ai CAS su computer, le calcolatrici
grafiche non hanno, almeno per ora, la possibilità di visualizzare
direttamente grafici di curve in forma implicita in modo agevole.
È possibile però ovviare all’inconveniente ricorrendo alla rappresentazione in forma parametrica, anche in forma del tutto trasparente allo studente.
RIFERIMENTO
DIFFICOLTÀ
STRUMENTO
/documen/italia/labclass/r * con le calcolatrici CG
cagn01.PDF
grafiche e con CGS
/documen/italia/cattolica/
quelle simboliche
tomas.PDF
* con un altro CAS CAS GD
/documen/italia/altro/con
iche.PDF
/documen/italia/libro_b/T
icap10.PDF
Viene riportato il testo di una scheda di laboratorio per una “esplorazione guidata” sulle parabole.
Vogliamo indagare sul fascio di parabole avente equazione:
38
y = ax2 + 3x + 2
Per studiare l’influenza del parametro a possiamo tracciare il grafico
dell’insieme di parabole con a che assume, ad esempio, valori interi
da 5 a 5.
Nell’ambiente di calcolo digitare seq(a,a,-5,5) [ENTER].
Viene così creata una lista formata dai valori interi non minori di 5
e non maggiori di 5.
Premere [2nd] [ANS] [STO] v [ENTER].
La lista precedente viene così assegnata ad una variabile di nome v.
Premere [APPS]Y= Editor per passare all’ambiente di editor di
funzioni. Premere [ENTER] per passare alla linea di editing e digitare:
v*x^2+3x+2 [ENTER].
La funzione (o, meglio, la lista di funzioni, una per ciascun valore
contenuto nella lista v) viene così posta nella corrispondente linea
dell’editor, contrassegnata sulla sinistra dal simbolo 9; ciò significa
che la funzione è attiva e quindi il suo grafico sarà tracciato non appena si passerà all’ambiente di grafica.
Premere [APPS] Graph per attivare lo schermo grafico. Saranno così tracciate, una dopo l’altra, le parabole della lista.
L’immagine così ottenuta offre alcuni spunti di indagine e ci permette di fare alcune osservazioni e congetture.
ƒ Perché alcune parabole hanno la concavità rivolta verso il
basso e altre verso l’alto?
ƒ Perché nel “fascio” tracciato compare anche una retta?
39
ƒ Sembra che tutte le parabole passino per lo stesso punto
dell’asse y. È vero? Se è vero, quali sono le sue coordinate?
E perché sono proprio quelle?
ƒ Sembra anche che tutte le parabole abbiano la stessa retta
tangente, passante per il punto di cui sopra. È vero e perché?
Se è vero, qual è la sua equazione?
ƒ Formulare una congettura che generalizzi il risultato ora trovato e dimostrarla. 3
ƒ Qual è il luogo dei vertici delle parabole?
Un altro esercizio, simile al precedente:
Vogliamo indagare sul fascio di parabole avente equazione:
y = x2 + bx + 2.
Per studiare l’influenza del parametro b possiamo tracciare il grafico
dell’insieme di parabole con b che assume, ad esempio, valori interi
da 5 a 5.
Usando il metodo visto nel precedente esempio ed utilizzando la medesima lista v, si ottiene il seguente grafico:
Potranno poi essere sottoposti agli studenti quesiti analoghi ai precedenti.
3
Nota per l’Insegnante: questa è probabilmente la domanda più difficile
(ma non al di fuori della portata degli alunni); si tratta di congetturare e successivamente dimostrare che la parabola di equazione y = ax2 + bx + c ha,
nel suo punto di intersezione con l’asse delle ordinate, la retta tangente di
equazione y = bx + c.
40
UNA PROPRIETA’ DELLE CUBICHE
ARGOMENTO E CLASSE
Esplorare, congetturare, dimostrare. Secondo Biennio.
POSSIBILITÀ D’USO
Uno strumento di calcolo, meglio se simbolico, è una formidabile
“macchina per fare congetture”: la possibilità di fare moltissimi esempi in pochi minuti e senza doversi preoccupare delle difficoltà
del calcolo permette di esplorare situazioni, formulare congetture,
verificarle o confutarle.
COMMENTI
In questo caso, più che con un vero e proprio argomento, si ha a
che fare con una strategia didattica, quella della scoperta (più o
meno) guidata. Con questa strategia il ruolo dell’insegnante è apparentemente meno importante ma in realtà è essenziale nel proporre
situazioni da esplorare, nel guidare la “ricerca” degli studenti, nello
stimolare il loro senso critico.
Questa strategia richiede più tempo rispetto alle lezioni frontali
tradizionali, ma, almeno per alcuni argomenti, è opportuno che
venga applicata: i risultati in termini di interesse, partecipazione,
coinvolgimento (e di conseguenza anche di qualità di
apprendimento) ripagheranno ampiamente il tempo impiegato.
RIFERIMENTO
DIFFICOLTÀ
STRUMENTO
/documen/italia/libro_b/ Dipende dal tipo CG CGS CAS
Ticap06.PDF
di applicazione
Iniziamo con un semplice problema, apparentemente di ordinaria
amministrazione, adatto ad alunni di quarta o quinta superiore: trovare l’equazione della retta tangente al grafico della funzione polinomiale
f(x) := x3 + 2x2 x 2
nel punto avente ascissa (x1 + x2)/2, ove x1 e x2 sono i primi due zeri
della funzione (in ordine crescente).
Tracciare il grafico della funzione e della retta tangente.
Il problema è molto facile anche “fatto a mano”: gli zeri sono, in
ordine crescente, 2,1,1; la retta tangente al grafico della funzione
41
ha coefficiente angolare f ’(3/2) = 1/4 e la sua equazione è y =
1/4x +1/4.
Con la TI-92 gli zeri possono essere trovati, ad esempio, con la
funzione zeros(x^3+2x^2-x-2,x) che fornisce la lista degli
zeri richiesti; la funzione zeros può essere digitata direttamente nella
linea di editing dell’ambiente di calcolo oppure la si può ottenere
premendo in successione i tasti F2 4.
Premere [APPS]Y= Editor. Premere [ENTER] per passare alla
linea di editing e digitare la funzione proposta: x^3+2x^2-x-2
[ENTER]. Premere [APPS]Graph per passare all’ambiente di grafica. Il grafico della funzione viene automaticamente tracciato. È
possibile modificare la scala: premere [F2] 2:ZoomIn per ingrandire l’immagine e premere ENTER per confermare il medesimo centro dello schermo (l’origine).
Il grafico appare nella nuova scala.
Premere [F5] A:Tangent. Viene così attivato il menu Math
alla voce Tangent. Viene richiesto Tangent at? È possibile spostare il
cursore grafico fino al punto desiderato, oppure, e in questo caso è
preferibile, si può digitare la sua ascissa direttamente: -3/2 [ENTER]. La retta tangente viene tracciata sullo schermo e la sua equazione (nella forma y = 0.25x + 0.25) appare in basso sullo schermo
(vedi figura 1).
Fig. 1
Fig. 2
Dal grafico appare un fatto inaspettato: la retta passa per il punto di
coordinate (1, 0), cioè per il terzo zero della funzione!
Forse è solo un caso fortuito: proviamo con un altro punto medio
tra gli zeri della funzione, per esempio con 0.
42
Premere [F4]. Questo tasto corrisponde al comando ReGraph: lo
schermo grafico viene cancellato e la funzione attiva viene ridisegnata senza alcun altro elemento aggiuntivo (in questo caso senza la retta tangente).
Premere [F4]A:Tangent poi premere 0 [ENTER] . La tangente
e la sua equazione, y = x 2, appaiono sullo schermo. Ancora la
tangente passa per lo zero x = 2.
Ma forse questo accade solo con questa funzione: proviamo con
un altra funzione polinomiale di terzo grado.
Premere [APPS]Y= Editor [F5]2 per attivare l’ambiente di
editor di funzioni e attivare il comando All Functions Off: tutte le
funzioni presenti, pur non essendo cancellate, vengono deselezionate: il simbolo 9 alla loro sinistra scompare ed il loro grafico non sarà
più tracciato. Premere il bottone direzionale verso il basso per portarsi sulla nuova funzione y2=, premere [ENTER] per passare alla linea di editing e digitare la funzione x^3+x^2-6x [ENTER]. Premere [APPS]Home per passare all’ambiente di calcolo, premere
[F2]4:zeros, digitare y2(x),x) [ENTER]: gli zeri della nuova funzione appaiono sulla destra dello schermo. Essi sono, in ordine
crescente, x1= 3, x2 = 0, x3 = 2.
Premere [APPS]Graph per tornare nell’ambiente di grafica e,
immediatamente dopo, premere [ON]. TI-92 traccia automaticamente il grafico delle funzioni attive non appena si è nell’ambiente di
grafica; premendo il tasto [ON] questa operazione viene interrotta.
Premere [F2]6:ZStndard: il grafico della funzione viene così
tracciato con la scala ai valori standard. Premere [F5]A:Tangent
e digitare -1/2 [ENTER]. Ancora una volta la retta tangente al grafico della funzione nel punto di ascissa (x1+x3)/2 passa per x2. Analogamente anche la retta tangente al grafico nel punto di ascissa
(x1+x2)/2 passa per x3 e così via.
Possiamo tentare ancora nuovi esperimenti con altre funzioni (ad
esempio f(x) := x3 2x2 4x + 8) anche con due zeri coincidenti (il
caso con tre zeri coincidenti è ovvio): otterremo sempre lo stesso risultato.
Ciò ci induce a formulare la seguente congettura:
43
In ogni funzione polinomiale di terzo grado con tre zeri reali (non
necessariamente distinti) a, b, c, la retta tangente al suo grafico nel
punto di ascissa (a+b)/2 passa per il punto (c,0).
Ma, lo abbiamo visto negli esempi precedenti, in matematica gli
esperimenti non bastano: è necessario procedere ad un dimostrazione
rigorosa di questa proprietà. Questa dimostrazione non è concettualmente difficile: basterà una verifica che però richiede una discreta
quantità di calcoli piuttosto noiosi, ma, avendo a disposizione una
calcolatrice simbolica, possiamo demandarle il lavoro più faticoso.
Premere [APPS]Home per tornare all’ambiente di calcolo e digitare
define f(x)=k*(x-a)*(x-b)*(x-c) [ENTER].
Non va omesso il simbolo * di moltiplicazione tra i fattori, in particolare quello dopo il coefficiente k. La funzione f(x) sarà così definita come funzione polinomiale avente zeri uguali, rispettivamente,
ad a, b, c. Il modo più semplice per ottenere l’equazione della retta
tangente al suo grafico nel punto x0 è quello di usare la funzione predefinita taylor . Digitare taylor(f(x),x,1,(a+b)/2) [ENTER]. Premere [F2]2 [2nd] [ANS][ENTER]. Come è noto, con
[F2]2 si attiva il comando factor; con [2nd] [ANS] si richiama il
precedente risultato; è poi necessario chiudere la parentesi.
Fig. 3
Fig. 4
Il polinomio di Taylor prima ottenuto viene così scomposto in fattori: la presenza del fattore (x c) ci assicura l’appartenenza del punto di coordinate (c, 0) alla retta tangente al grafico della curva nel
punto considerato.
44
DUE PROBLEMI DI GEOMETRIA
ARGOMENTO E CLASSE
Esplorare, congetturare, dimostrare.
Primo Biennio.
POSSIBILITÀ D’USO
Le osservazioni fatte nella precedente scheda sono valide anche in
un contesto geometrico, in particolare usando un software di geometria dinamica come Cabri Géomètre, anche nella versione implementata sul alcune calcolatrici tascabili.
COMMENTI
V. scheda precedente.
RIFERIMENTO
DIFFICOLTÀ
STRUMENTO
/documen/italia/labclass/ Dipende dal tipo CGS GD
pacco02.PDF
di applicazione
Esplorare, congetturare, dimostrare con la TI-92 : due problemi
di geometria.
(P. Accomazzo)
L’attività a cui si farà riferimento è stata condotta in una classe II
Liceo scientifico con sperimentazione PNI. Gli allievi erano 27 ed
avevano a disposizione 16 calcolatrici. Nell’ambito della geometria
euclidea avevano studiato le proprietà dei quadrilateri ed avevano affrontato alcune dimostrazioni sull’argomento; conoscevano la teoria
relativa al teorema di Talete, ma non avevano svolto ancora esercizi
in proposito. In ambito cartesiano sapevano lavorare su segmenti
(pendenza, lunghezza, punto medio) e su rette (equazione, intersezione). Avevano pratica del software Cabri 1, che usavano in laboratorio di Informatica4
È stato proposto agli allievi il seguente problema aperto :
Costruisci un generico quadrilatero ABCD.
Indica con M, N, P, Q i punti medi dei lati AB, BC, CD, DA.
4
L’esperienza prende spunto dalle attività del Seminario di geometria per la scuola superiore
coordinato dal Prof. Arzarello del Dipartimento di Matematica dell’Università di Torino.
45
Costruisci il quadrilatero MNPQ ; si tratta di un quadrilatero
particolare ?
MNPQ può essere un rettangolo, o un rombo o un quadrato ?
Formula una congettura sulle caratteristiche di MNPQ in relazione alla particolare forma di ABCD.
Dimostra le tue affermazioni con le proprietà della geometria
euclidea.
La costruzione del disegno con la TI-92 è molto semplice : con
[APPS] Geometry New , assegnato un nome al file, si entra in
ambiente Geometry, ci si serve quindi dei comandi [F2] segment
ed [F4] midpoint per avere la figura richiesta. ( Fig. 1).
Fig. 1
Fig. 2
Muovendo i punti del quadrilatero ABCD si ottiene ancora una
figura che mantiene le relazioni geometriche richieste : si può quindi
dire di avere a disposizione un’intera classe di figure che rispondono
ai requisiti del problema.
Gli studenti, lavorando a coppie, hanno individuato abbastanza
agevolmente la relazione di parallelismo tra i lati di MNPQ. Alcuni
hanno ritenuto opportuno introdurre la misura di alcuni lati (si ottiene
con [F6] distance) che, pur con qualche imprecisione legata
alle modalità di misura di Cabri, dava un’idea della congruenza fra
segmenti. Più difficile è stata invece la ricerca delle condizioni di
ABCD che davano origine ad un particolare parallelogrammo
MNPQ: alcuni allievi si sono fermati a situazioni particolari, affermando, ad esempio che:
x perché MNPQ sia un rombo, ABCD deve essere un rettangolo,
x perché MNPQ sia un rettangolo, ABCD deve essere un rombo.
46
In questi casi è stato utile “muovere” i vertici di ABCD mostrando situazioni più generali che davano origine a particolari quadrilateri interni.
Dimostrare che MNPQ è un parallelogramma non ha creato difficoltà: alcuni studenti hanno intuito l’utilità di tracciare la diagonale
AD ed hanno comunicato ai compagni la scoperta. Questa modifica
grafica ha facilitato la scoperta di relazioni tra lati di MNPQ e diagonali di ABCD ed ha fatto sì che alcuni allievi riformulassero le congetture relative alla seconda parte del problema. Per poter individuare più facilmente le situazioni particolari , qualche gruppo ha ritenuto
opportuno introdurre la misura di lati o angoli che, pur con qualche
imprecisione legata alle modalità di misura di Cabri, dava un’idea
per la ricerca della congruenza (Fig. 2).
L’attività si è conclusa con una discussione in cui si mettevano in
comune gli elementi acquisiti e quelli dubbi; gli allievi hanno quindi
stilato individualmente una dimostrazione che io ho ritirato e corretto.
A distanza di una settimana è stato proposto un altro problema :
È dato il triangolo rettangolo ABC di ipotenusa BC. Costruisci sui cateti, esternamente ad ABC, i due quadrati ACTS e
APQB.
In che relazione sono i punti Q, A,T?
In che relazione sono le rette PB ed SC?
Di che natura è il quadrilatero PBCS ? Può essere un parallelogramma?
Dimostra le tue affermazioni scegliendo l’ambiente della geometria euclidea o l’ambiente della geometria analitica.
Fig. 3
Fig. 4
47
Alcuni allievi hanno scelto di “immergere” la figura in un piano
cartesiano ([F8] Format Coordinate axes Rectangular ), rilevando le coordinate di alcuni punti.
Si è scelto di non introdurre la verifica automatica dell’allineamento
o del parallelismo che Cabri2 prevede (F4] check property ).
Anche questa attività si è conclusa con un’ampia discussione e con
la correzione delle dimostrazioni prodotte individualmente.
Al termine è stata svolta una verifica individuale in cui ogni allievo
aveva a disposizione una TI-92 su cui erano state memorizzate le figure relative alle due attività di gruppo.
Per concludere: Cabri2 su Personal Pomputer è certo più agile nel
dragging e più incisivo nella grafica rispetto all’analogo software
della TI-92. Quest’ultimo ha, tuttavia, il grosso pregio del rapporto 1
a 1 studente-macchina, della disponibilità immediata durante le lezioni e della possibilità d’uso durante le verifiche individuali.
48
LE EQUAZIONI DI UN ORSETTO
ARGOMENTO E CLASSE
Curve in forma parametrica. Secondo Biennio.
POSSIBILITÀ D’USO
Definizione, tabulazione, rappresentazione grafica e manipolazione
di curve in forma parametrica.
COMMENTI
Argomenti come la rappresentazione di curve in forma parametrica
(e anche in coordinate polari) sono normalmente poco presenti nella prassi didattica della scuola secondaria; causa di ciò è anche la
difficoltà nell’ottenere una loro rappresentazione se non attraverso
il passaggio alla equivalente forma cartesiana. Gli strumenti tecnologici permettono di ottenere i loro grafici in modo molto semplice.
RIFERIMENTO
DIFFICOLTÀ
STRUMENTO
/documen/italia/montesil Dipende dal tipo CGS CAS
v/impedovo.PDF
di applicazione
Curve in forma parametrica: gli Orsetti
(S. Cappuccio, da un’idea di Michele Impedovo)
Un argomento di geometria analitica spesso un po’ trascurato nella prassi scolastica è quello delle curve rappresentate in forma parametrica, in particolare il caso della circonferenza. Anche in questa
occasione può essere preziosa la disponibilità di una calcolatrice grafica che ha la possibilità di tracciare facilmente il grafico di una curva rappresentata nella forma x = f(t), y = g(t).
Invece di proporre esercizi formulati con il solito linguaggio un
po’ pedante che si trova sui libri di testo (Trovare l’equazione parametrica della circonferenza avente il centro in… e raggio ….) si potrebbe procedere in altro modo.
In “La matematica nella scuola di tutti: percorsi didattici e ipotesi
di rinnovamento” di M. Impedovo, Atti del Congresso ADT 2000
(Montesilvano) incontriamo un accenno a una immagine creata da un
suo fantasioso studente; trovando la cosa divertente e utile, ho proposto qualcosa di simile anche ai miei studenti (terza Istituto Tecnico) ,
invitandoli a riprodurre il disegno in Fig. 1.
49
Fig. 1. L’orsetto base, altrimenti Fig. 2. Le equazioni parametrinoto come l’Orsetto Alche dell’Orsetto Allegro
legro
Gli studenti conoscevano solo le equazioni parametriche della circonferenza di raggio unitario e centrata nell’origine.
Tutti, senza difficoltà, anche grazie al lavoro precedente sulle trasformazioni elementari, sono arrivati da soli a scoprire come ottenere
le equazioni parametriche di una circonferenza con un dato centro e
un dato raggio per costruire così naso, occhi e orecchie. Particolarmente interessante è stata l’osservazione del comportamento degli
studenti nel posizionamento delle orecchie: è stato in certi casi consapevole e teorico/razionale, determinando l’intersezione tra la circonferenza di equazione x2 + y2 = 16 (la testa dell’orsetto) e le bisettrici dei quadranti, in altri casi più sperimentale/bricoleur, ad esempio posizionando il cursore sullo schermo nella posizione voluta e
leggendo le coordinate del punto di tangenza sullo schermo, ma comunque tutti sono arrivati al risultato voluto; i più raffinati hanno
addirittura utilizzato le simmetrie per disegnare il secondo occhio e il
secondo orecchio.
Più difficile è stata la determinazione delle equazioni del “sorriso”: trattandosi di una semicirconferenza e dato che con lo strumento
utilizzato (la calcolatrice TI-92) il parametro t deve variare nel medesimo intervallo per tutti i grafici rappresentati nello stesso schermo,
in alcuni casi (meno del previsto, bisogna dire) è stato necessario
l’intervento dell’insegnante.
Possibili variazioni sul tema e approfondimenti: Orsetto Triste, Orsetto Serio, Orsetto Serio seconda versione (notare le orecchie, non
facili), rappresentati rispettivamente in Figg. 3a, 3b, 3c.
50
Fig. 3°
L’Orsetto Triste
Fig. 3b.
L’Orsetto Serio
Fig. 3c.
L’Orsetto Serio
seconda versione
(si faccia attenzione alle orecchie)
51
INTRODUZIONE ALLE SUCCESSIONI
ARGOMENTO E CLASSE
Esempi significativi di successioni, approccio intuitivo al concetto di limite. Secondo Biennio.
POSSIBILITÀ D’USO
Costruzione e esplorazione del comportamento di successioni.
COMMENTI
Ciò può essere fatto, per le successioni ricorsive, sfruttando la possibilità di utilizzare il risultato del precedente calcolo (ANS(1)) oppure l’apposito ambiente di definizione delle successioni. In questa
sede viene presentato un lavoro svolto nell’ambito della sperimentazione ministeriale Labclass.
RIFERIMENTO
DIFFICOLTÀ STRUMENTO
/documen/italia/labclass/ **
CGS
atrav01.PDF
UN APPROFONDIMENTO SULLE PROGRESSIONI GEOMETRICHE
(A. Travaglini)
Classe 4B.
Finalità perseguite:
usare la TI-92 per far acquisire i concetti di successione e di progressione.
Argomenti trattati:
successioni e progressioni geometriche.
Obiettivi usare la TI-92 per:
- recuperare gli alunni più deboli dando loro un punto di appoggio per superare le difficoltà;
- abituare gli studenti a scegliere la strategia risolutiva più adatta al problema;
- risolvere problemi sulle successioni e sulle progressioni.
Metodologia:
- uso del view screen per l'esposizione e i richiami dei concetti
fondamentali;
52
-
uso di una macchina TI-92 per ogni studente per un lavoro
autonomo che rispetti i tempi di apprendimento di ciascuno;
- scoperta guidata di leggi e proprietà con eventuali discussioni
sulle difficoltà incontrate dall'alunno.
Tempi di attuazione:
sei ore.
Prima lezione due ore.
Obiettivo:
rappresentare l'andamento della successione an = (3n +1) / (2n + 3),
per far comprendere agli alunni le successioni convergenti, divergenti e indeterminate.
Strumenti utilizzati: view screen e calcolatrice grafica TI-92.
Da quanto si vede sullo schermo si può notare la scrittura della successione.
Per visualizzare questa schermata bisogna eseguire i
seguenti comandi:
MODE imposta il modo Graph
su SEQUENCE e poi <ENTER> e ancora < ENTER>
53
iW per scrivere la successione.
F6 e poi 3 per definire lo stile
della rappresentazione. iE per
aprire la finestra Window Editor:
dove si possono impostare le opportune variabili, (vedi figura seguente).
Così facendo si dà l'opportunità
alla TI-92 di rappresentare il grafico degli elementi di una successione. Andando in modalità grafica: iR e usando F2 Zoom si visualizzano i punti.
Si costruisce una tabella nella
quale sono elencati gli elementi
delle successione operando nel
modo seguente:
iT : si apre una finestra nella
quale puoi impostare la costruzione della tabella, si inseriscono
i valori come in figura accanto e
poi si digita <ENTER>.
Con iY compare una tabella con
i primi 8 valori della successione,
premendo [2nd] e il cursore verso il basso si possono visualizzare
gli altri valori della tabella, come
mostrano le figure successive.
Procedendo sempre tenendo premuto [2nd] e il cursore verso il
basso si possono visualizzare altre pagine, oppure con iT si riapre la finestra nella quale si può
inserire il valore di 200 a tblStart
e ottenerre la seguente schermata,
54
nella quale si nota che all'aumentare di n la successione si avvicina al valore di 1,5, pertanto si
tratta di una successione convergente.
ESERCIZI:
Studiare le successioni :
a) an = (n^2-2) / n ;
b) bn = (n + (-1) ^ n * n ) / ( n / 2 ).
- Rappresentare tali successioni sullo schermo e descrivere tutte le
sue caratteristiche.
- Costruire le relative tabelle variando opportunamente i valori iniziali di tblStart.
A quale successione si riferisce il seguente grafico e quali sono i valori
inseriti nella finestra di Window
Editor ?
A quale successione si riferisce la
seguente tabella e quali sono valori
inseriti nella finestra Table Setup ?
Osservazioni :
Al termine di queste due ore gli alunni hanno:
- acquisito i concetti di successione convergente, divergente e
indeterminata e acquisito maggiore dimestichezza con i comandi della TI-92;
- imparato a porsi domande, sia di fronte al grafico dei punti
della successione che di fronte alla tabella dei valori, a ipotizzare risposte e a verificarle.
55
DISTRIBUZIONE DELLE FREQUENZE
ARGOMENTO E CLASSE
Dati e previsioni: distribuzione delle frequenze, rappresentazioni grafiche, principali indici statistici. Primo Biennio.
POSSIBILITÀ D’USO
L’uso di uno strumento di calcolo è essenziale per affrontare esempi significativi in campo statistico, senza disperdersi in facili quanto pesanti calcoli, assolutamente inutili dal punto di vista dell’apprendimento.
COMMENTI
Le calcolatrici o il foglio elettronico, hanno già predefiniti i comandi per realizzare istogrammi e altre rappresentazioni grafiche.
RIFERIMENTO
DIFFICOLTÀ STRUMENTO
/documen/italia/montesil **
CNG CGS FE
v/carosati.pdf
Da “Probabilità e Statistica con la TI-92” di L. Carosati in “Atti del
2° Convegno Nazionale ADT”, Montesilvano 2000
Distribuzione delle frequenze
(L. Carosati).
La Statistica e la Probabilità sono ancora una specie di Cenerentola nell'ambito dei nuovi programmi del PNI essendo argomenti ancora piuttosto nuovi dal punto di vista della tradizione didattica a livello di scuola media superiore, e non molto conosciuti dagli insegnanti,
specie quelli che non hanno ricevuto a suo tempo all'Università una
formazione specifica. Essi vengono quindi relegati (talvolta anche
nei libri di testo) a poche nozioni un po' frettolose e confuse anche
perché in questo quadro si preferisce dedicare il prezioso tempoclasse ad altre questioni più tradizionali e consolidate. Lo stesso MPI
ha dimostrato nelle prove d'esame una certa incertezza presentando
problemi da cui non si evince chiaramente quali siano gli obiettivi
fondamentali che gli studenti debbono raggiungere.
La presente comunicazione vuole dare qualche contributo verso
l'introduzione dei due argomenti in modo un po' più organico e più
56
adatto al livello degli studenti di scuola media superiore (per i primi
concetti si può già lavorare nella prima classe), anche attraverso l'uso
della TI-92 che con le sue potenzialità diventa indispensabile strumento attraverso cui elaborare i concetti.
Per un approfondimento, in particolare tecnico, si fa riferimento a
[9] in Bibliografia.
Introduzione ai concetti statistici.
1.1 Un po' di Statistica …
1.1.1. Un problema di medie.
L'iter Statistica-Probabilità può cominciare dalla Statistica
attraverso l'analisi di semplici problemi di medie. Ad esempio si può
chiedere alla classe di determinare il peso medio degli alunni della
classe stessa o di due o tre classi (più sono i dati più si giustifica e si
apprezza l'uso di strumenti automatici di calcolo). Il problema è
semplice ma coinvolge già alcuni concetti importanti: si tratta di
raccogliere i dati di una variabile continua, di decidere quindi come
approssimare le misurazioni, poi di definire il concetto di valore
medio per arrivare alle formule delle medie aritmetiche semplice e
ponderata.
1.1.2. La TI-92, gli istogrammi e le variabili statistiche.
Si può anche lavorare con la TI-92 introducendo i dati in una
tabella (un semplice elenco) e poi farli rappresentare con un
istogramma (Fig. 1). La TI-92 può rappresentare un diagramma a
bastoni (a nastri) ma meglio ancora un istogramma: in questo caso
calcola automaticamente le frequenze dei vari pesi suddividendo i
dati in un certo numero di classi deciso dall'utente. Con qualche
accorgimento si possono anche decidere i valori iniziali e finali delle
classi.
57
Fig. 1 - Istogramma della distribuzione dei pesi.
Questa possibilità favorisce l'apprendimento del concetto di
distribuzione delle frequenze. Osservando l'istogramma ci si chiede
che cosa è successo, ed esplorando con il cursore i vari rettangoli
dell'istogramma si scoprono appunto le frequenze usate dalla
macchina.
È naturale introdurre allora il concetto di variabile statistica come
corrispondenza tra valori del carattere (o classi, o valori
rappresentativi delle classi) e frequenze. Non è difficile poi passare
alle frequenze relative. Tutto ciò è facilmente elaborabile con la TI92.
1.1.3. Media ponderata e varianza.
Successivamente si può far calcolare non solo la media dei dati,
ma anche lo scarto quadratico medio (e quindi la varianza) e altri
valori statistici (Fig. 2).
Fig. 2 - Calcolo di media e scarto quadratico medio con la TI-92.
Il fatto di farlo fare prima alla TI-92 e poi di indovinare che cosa
ha fatto e cercare di riprodurlo costituisce un elemento di sfida per
gli alunni, e questo facilita ed accelera l'apprendimento. Un
accorgimento: quando si cerca di indovinare cosa fa la macchina è
58
bene semplificare il problema ad esempio diminuendo il numero di
dati in modo da renderlo accettabile per una elaborazione pressoché
manuale. È il caso anche di fare diverse prove in situazioni di
estrema regolarità, come ad esempio dati tutti uguali o con valori
concentrati agli estremi della distribuzione. Tutto ciò permetterà poi
di capire meglio anche l'elaborazione teorica, ad esempio il concetto
di valore medio visto come quel valore che può sostituire tutti gli
altri dando lo stesso risultato complessivo.
In poco tempo quindi, e magari con problemi legati alla vita degli alunni (tipico è il problema del trattamento statistico dei voti - voto
medio, scarti, mediana e quartili ecc.) si può superare il primo impatto con la Statistica.
59
DALLA STATISTICA ALLA PROBABILITA’
ARGOMENTO E CLASSE
Dati e previsioni: Dalla statistica alla probabilità. Primo Biennio.
POSSIBILITÀ D’USO
Nell’ambiente Data/Matrix della calcolatrice vengono simulati eventi casuali per introdurre i concetti di probabilità e di variabile
aleatoria..
COMMENTI
La calcolatrice (come anche il foglio elettronico) consente un approccio “sperimentale”alla probabilità. Attraverso la simulazione di
un evento casuale è possibile introdurre i concetti di probabilità
classica e frequentista e arrivare alla formulazione della legge dei
grandi numeri.
Viene riportata una parte di un’esperienza realizzata all’interno del
progetto Labclass e contenuta nel CD di ADT
RIFERIMENTO
DIFFICOLTÀ STRUMENTO
/documen/italia/labclass/ **
CNG CGS FE
lcaro01.pdf
Dalla statistica alla probabilità
(L. Carosati)
Il concetto di variabile aleatoria è piuttosto oscuro (e astruso) se
presentato in modo formale partendo da situazioni solo probabilistiche, in particolare fatte di Teste e Croci, palline Bianche e Nere, soprattutto non se ne comprende l'utilità quando tutto sommato per calcolare la probabilità degli eventi basta appunto il concetto di "evento".
Un'idea per superare l'ostacolo è quella di introdurre la probabilità
dopo la statistica, partendo inizialmente da un fenomeno statistico in
cui già il concetto di variabile statistica è stato acquisito.
Problema 1 : "facciamo lanciare un dado dalla …TI-92 !"
60
All'inizio si introduce la funzione Rand(n) della TI-92 e si prende
confidenza con il concetto di numero aleatorio (basta chiamare i ragazzi per l'interrogazione utilizzando tali numeri della TI-92 invece
del solito numero di pagina, tutt'altro che equanime).
Poi si passa alla simulazione, in una tabella, del lancio di un dado
(30 lanci sono sufficienti).
Si ha così una tabella di dati (aleatori) che possono essere
elaborati esattamente come quelli di una tabella statistica (si cercano
le frequenze di uscita delle varie facce).
Concetti introdotti: numeri casuali e pseudo-casuali, probabilità.
Con [APPS] DATA/Matrix Editor DADO si apre una
nuova tabella5 .
Introdurre nella colonna C1 la formula seq(rand(6),x,1,30) per generare una lista di numeri casuali.
Elaborare la tabella come quella dei pesi (vedi le indicazioni
per PESI e le figure del paragrafo 1).
Le figure relative alla tabella DADO sono le seguenti:
5
DATA/MATRIX EDITOR: se succede di dover cancellare delle colonne, per errori di impostazione della tabella, accade che si blocca il calcolo sulla prima formula che non trova più i riferimenti corretti. In questo caso da F1 (di DATA EDITOR) disattivare l’Auto-calcolo (opzione
9:Format…), poi modificare tutte le formule delle varie colonne ed infine riattivare l’Autocalcolo.
61
È bene osservare anche l'istogramma.
Ad ogni rientro nella tabella ([APPS]Data/Matrix
Editor) i lanci vengono ripetuti e così si può notare che le uscite
delle varie facce non sono sempre in egual numero.
Dopo aver osservato vari istogrammi si pongono i due problemi:
Problema 2 : "se punto 1000 lire sul 3 quanto punteresti tu sul 6 ?"
Problema 3 : "c'è una faccia su cui ti senti di puntare di più ?"
La discussione in genere si accende perché non per tutti è naturale
pensare che non ci sono preferenze particolari per assegnare un maggior grado di fiducia ad una delle facce. Nonostante accada che le
uscite cambino continuamente, per alcuni qualche faccia potrebbe
presentarsi più facilmente.
In effetti tale posizione concettuale non è peregrina perché la TI92 non effettua un vero lancio "casuale", ma una semplice simulazione attraverso un algoritmo di calcolo. Questa posizione dubbiosa è
utile però per presentare la differenza tra i numeri casuali e quelli
pseudo-casuali che dei primi mantengono solo la pressoché uniforme
distribuzione su un grande numero di lanci.
Tutti si convincono in genere che nel caso del lancio di un vero
dado non ci sono motivi particolari per assegnare la preferenza ad
una faccia invece che ad un'altra.
Tuttavia anche questa equidistribuzione ipotetica delle uscite è
una semplice congettura, un grado di fiducia assegnato alle varie
facce.
Si arriva così ai vari concetti di probabilità:
i classica : spontanea e intuitiva
i soggettiva : non si hanno motivi per ritenere una faccia più probabile delle altre (probabilità = grado di fiducia)
i frequentista : si arriva ad 1/6 notando (legge empirica del caso)
la tendenza alla coincidenza delle frequenze aumentando il numero di lanci.
62
La conclusione è che possiamo esaminare i fenomeni non solo
dopo che si sono verificati (statistica) ma anche prima che si verifichino o, pur essendosi verificati, in assenza di informazioni deterministiche sugli eventi stessi (probabilità)6.
Avremo ancora variabili , non più statistiche ma casuali, popolazioni ed unità (universo degli esiti, eventi), valori di sintesi e dispersione (media, varianza, sqm): la probabilità è un numero che svolge
lo stesso ruolo della frequenza relativa, le facce del dado sono come
le persone di cui rileviamo il peso (eventi), i valori disegnati sulle
facce del dado sono i valori possibili di una variabile (aleatoria) come quelli di una variabile statistica (il peso), la tabella che ad ogni
valore della faccia assegna una probabilità è l'equivalente della tabella di distribuzione delle frequenze.
Il ponte dalla statistica alla probabilità e alle variabili casuali è
stato gettato: si tratta ora solo di sviluppare il discorso.
6
Ad esempio se lancio un dado e non guardo quale faccia è uscita (potrei spegnere la luce !)
l’evento si è verificato comunque ma non ho informazioni deterministiche che mi permettono
di individuare il numero uscito. Ho solo informazioni non deterministiche, cioè il fatto che il
dado ha sei facce ma nient’altro. Per questo motivo sarebbe indifferente puntare su una faccia
prima o dopo il lancio, purché nel secondo caso non si conosca quale faccia è uscita.
63
REGRESSIONE E CORRELAZIONE
ARGOMENTO E CLASSE
Dati e previsioni: concetto e significato di modello, curve di regressione. Secondo Biennio.
POSSIBILITÀ D’USO
Lo studio di questo argomento rappresenta un caso emblematico di
enfatizzazione degli aspetti di calcolo, anziché di quelli concettuali.
L’attività presentata cerca di evidenziare come l’utilizzo di uno
strumento di elaborazione consente di focalizzare l’attenzione
sull’analisi della situazione a cui vengono applicati diversi modelli
di interpolazione.
COMMENTI
L’esempio qui proposto è stato sviluppato nell’ambito di una sperimentazione in alcune scuole secondarie nell’ambito di un progetto SET; è stato attuato utilizzando la calcolatrice numerica e grafica
TI-83, ma può essere realizzato anche con le altre calcolatrici grafico-simboliche, sia con l’apposito software Statistics sia senza.
RIFERIMENTO
DIFFICOL- STRUMENTO
Viene riportata parte di un’unità TÀ
CNG CGS FE
didattica tratta dal sito Cartesio: ***
http://www.cartesionline .it
/html/ set_ unita-stat00.html
Regressione e correlazione
(A. Orlandoni)
In questa attività vengono utilizzati i dati relativi al censimento
degli Stati Uniti (in milioni di persone):
Anno
X
Y
anno
X
Y
64
1810
1
1820
2
1830
3
1840
4
1850
5
1860
6
1870
7
1880
8
1890
9
7.24
9.64
12.87
17.07
23.19
31.44
39.82
50.16
62.95
1900
10
1910
11
1920
12
1930
13
1940
14
1950
15
1960
16
1970
17
1980
18
75.99
91.97
105.7
122.78
131.67
151.33
179.32
203.21
226.5
Il valore per il 1990 è di 249.63 milioni di persone, ma non lo
includeremo nella lista perché ce ne serviremo per verificare con
quale precisione l'equazione interpolante è in grado di prevederlo.
Costruzione della tabella e rappresentazione dei dati iniziali
La prima operazione necessaria è quella di memorizzare i dati
relativi alla popolazione in una lista (POPUS), e quelli relativi agli anni in un'altra (L1) utilizzando i valori da 1 a 18 per gli anni
dal 1810 al 1980 e rappresentarli in un diagramma a dispersione.
Premete [STAT]1:Edit. Osservate che ci sono sei nomi di
lista da L1 a L6. Inserite nella colonna L1 i valori relativi a X.
Evidenziate L2 e premete [2nd] [INS] per spostare la lista
L1 sulla destra. Per inserire il nome della seconda lista mettetevi
in modalità alphalock ([2nd] [ALPHA]) e scrivete POPUS.
Premete [ENTER] [p] e inserite i dati relativi alla popolazione.
Per rappresentare i dati in un grafico a punti è necessario predisporre la TI83. Premete [2nd] [Y=] ( Stat Plot) e selezionate la
modalità come in Fig. 2.
Fig. 1
Fig. 2
Premete [ZOOM] 9:ZoomList [TRACE] per ottenere il grafico mostrato IN Fig. 3
Fig. 3
65
Osservate che in cima alla schermata del grafico viene mostrata
l'impostazione con P1:L1,POPUS.
I punti sembrano giacere più su di una curva che non su di una linea
retta, ma noi cominceremo interpolando i dati con una curva di regressione lineare.
Retta di regressione lineare secondo i minimi quadrati
Per calcolare i coefficienti della retta interpolante premete
[STAT] [CALC] 4: LinReg(ax+b)L1,POPUS,Y1, con POPUS selezionato da [2nd][LIST] e Y1 da [VARS]Y-VARS
1:Function (vedi Fig.4). Per vedere i risultati premete [ENTER]
(Fig. 5).
Fig. 4
Fig. 5
Oltre all'equazione della retta di regressione vengono automaticamente calcolati sia il coefficiente di determinazione sia quello di
correlazione lineare come indicatori della bontà della funzione scelta.
Il coefficiente di determinazione è dato da
n
r2
¦ ( yˆ
yi ) 2
i
i 1
n
¦(y
,
i
y)
2
i 1
dove yˆ i
f ( x i ) rappresenta il valore teorico, corrispondente al da-
to xi, e y il valore medio dei dati sperimentali. Se la funzione si accosta in modo perfetto ai dati, cioè yˆ i y i per ogni i, allora la frazione assume il valore 0 e il coefficiente di determinazione il valore 1.
66
Viceversa, più il coefficiente di determinazione si avvicina a 0, meno
adatta è la funzione a rappresentare la serie di dati statistici.
Nel caso della retta si può anche calcolare il coefficiente di correlazione lineare:
n
r
¦ (x
i
x)( y i y )
i 1
n
¦ (x
,
2
i
x) ( y i y )
2
i 1
che varia fra 1 e 1; r = 1, indica una perfetta correlazione inversa, r = 0 indica che non vi è correlazione e r = 1 indica una perfetta
correlazione diretta.
Premete [ZOOM] 9:ZoomStat [TRACE] per visualizzare il
grafico della retta di regressione sovrapposta al diagramma dei dati
sperimentali (Fig. 6).
Fig. 5
Fig. 6
La TI-83, quando vengono calcolati i parametri della retta dei minimi quadrati, costruisce automaticamente una lista (RESID) in cui
vengono inseriti gli scarti residui, cioè le differenze fra i valori sperimentali e i valori teorici.
Se la funzione interpolante approssima in modo perfetto i dati, gli
scarti residui sono tutti nulli, altrimenti assumono valori diversi.
Quindi possiamo utilizzarli per avere un'informazione sulla "bontà"
dell'interpolazione scelta. Rappresentiamo quindi il grafico degli
scarti residui.
67
Per ottenerlo, dovremo prima disattivare gli altri grafici, poi impostare Plot2 sul diagramma a punti, dove Xlist:L1 e Ylist:RESID, come
nella figura 7.( Per disattivare il grafico della retta di regressione
premete [Y=], utilizzando il cursore posizionatevi sul segno = e
premete [ENTER]. Osservate che il segno = cambia forma)
La disposizione non casuale del grafico degli scarti residui conferma che la retta di regressione non interpola molto bene i dati. Poiché gli scarti residui risultano alcuni positivi, altri negativi ed altri
ancora uguali a zero, ci serviremo della Somma dei Quadrati degli
Scarti Residui per una valutazione di quanto i punti si adattino alla
curva; infatti questo valore sarebbe zero se tutti i punti giacessero
sulla curva. Il valore che si ottiene è 4651.51534, confermando il fatto che la retta non sia la funzione più adatta in questo caso ([2nd]
[LIST]MATH 5:sum , poi [2nd] [LIST]RESID).
Proviamo anche a "prevedere" il valore per l'anno 1990: [VARS]
Y-VARS 1:Function1:Y1 In figura 8 è stato anche calcolato
l'errore relativo sulla previsione, che risulta piuttosto grande (17%).
Fig. 8
Confronto fra diverse interpolazioni
Si può ripetere il procedimento interpolando i dati con funzioni
diverse (la calcolatrice offre la possibilità di usare molti modelli).
Come esemplificazione vengono riportati in una tabella i risultati
delle analisi fatte e dei calcoli svolti, in modo da poterli confrontare
meglio:
68
Interpolazione
lineare
quadratica
esponenz.
logistica
SQSR
4652
131
9849
307
% errore
su X=19
17.1
0.4
-48.3
2.9
Grafico dei residui Lungo periodo
schema delineato
sembra casuale
schema delineato
schermata 25
crescita lineare
" in prop. a x2
" esponenz.
si appiattisce
L'interpolazione quadratica sembra la migliore nel breve periodo,
ma la logistica non si discosta di molto e, ha il vantaggio di una
proiezione a lunga scadenza più realistica (almeno speriamo sia così!).
69
70
PER APPROFONDIRE
-
AA.VV., “Matematica 2003, Attività didattiche e prove di verifica per un nuovo curricolo di Matematica”, L. S. Vallisneri,
Lucca 2003.
-
AA.VV., “Il Progetto Labclass”, Quaderno n. 44, L. S. Ricci
Curbastro, Lugo di Romagna 2001.
-
G. C. Barozzi, S. Cappuccio, “Le calcolatrici grafiche
nell’insegnameno della matematica”, Pitagora Editrice, Blogna 1997.
-
M. Impedovo, “Matematica: insegnamento e computer algebra”, Springer-Verlag Italia, Milano 1999.
Inoltre:
-
IPOTESI, rivista quadrimestrale di Texas Instruments.
CD di ADT 2004, Ghisetti e Corvi ed.
http://www.adt.it/
http://www.cartesionline.it
http://www.fardiconto.it/index.htm
71