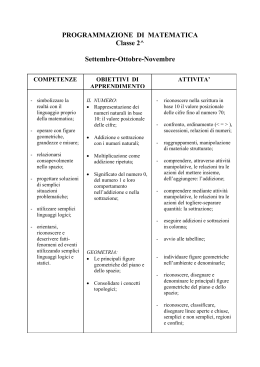
Relazione tra sottrazione e addizione nei numeri Interi
Relativi
Si è visto che il modello geometrico dell’addizione consente di addizionare o sottrarre due quantità
algebriche mediante la regola del parallelogrammo. Se si opera con i numeri Interi Relativi,
osserviamo che quantità algebriche di segno opposto sono addizionate mediante linee tracciate in
direzione opposta rispetto allo 0.
Inoltre, il modello geometrico della addizione/sottrazione è utile per giustificare e verificare una
importante relazione tra l’operazione di addizione e sottrazione nei numeri Interi Relativi e cioè che
la somma di una quantità a con una quantità opposta –b di una assegnata b, equivale alla sottrazione
tra la quantità a e quella assegnata b. In modo formale questa proprietà può essere espressa
attraverso la seguente identità: a  b  a  b .
La figura sotto riportata illustra questa proprietà