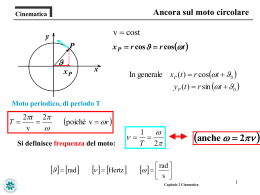
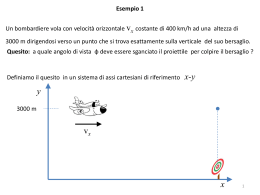
Agenda per oggi

Cinematica 2-D, 3-D
Pg 1
Cinematica 3-D
La posizione, la velocità e l’accelerazione di una particella in
3 dimensioni può essere espressa come:
r= xi+yj+zk
v = v x i + vy j + vz k
(i , j , k vettori unitari)
a = a x i + ay j + az k
Abbiamo già visto le equazioni della cinematica 1-D :
x  x(t )
dx
v
dt
dv d 2 x
a
 2
dt dt
Pg 2
Cinematica 3-D
Per 3-D, applichiamo semplicemente le equazioni 1-D a
ciascuna delle equazioni delle componenti.
x  x(t )
vx 
ax 
dx
dt
vy 
d2x
dt
y  y( t )
2
ay 
dy
dt
vz 
d2y
dt
z  z( t )
2
az 
dz
dt
d2z
dt 2
Queste possono essere combinate nelle equazioni vettoriali :
r = r(t)
v = dr / dt
a = d 2r / dt 2
Pg 3
GRANDE IDEA!!:
Trattare ciascuna componente del vettore
indipendentemente.
Per ottenere il moto completo in 3-D usiamo
semplicemente la matematica vettoriale per sommare le
componenti (SOVRAPPOSIZIONE).
Esempio: per accelerazione costante abbiamo :
a = const
v = v0 + a t
r = r0 + v0 t + 1/2 a t2
(dove a, v, v0, r, r0, sono tutti vettori)
Pg 4
Cinematica 2-D
Fissiamo la nostra attenzione sui problemi 2-D :
*L’aritmetica dei vettori in 2-D non è molto differente da quella in 3-D.
* I problemi 3-D possono essere ricondotti a problemi 2-D quando
l’accelerazione è costante:
Scegliere l’asse y lungo la direzione dell’accelerazione
Scegliere l’asse x lungo l’altra direzione del moto
Esempio: Lanciamo una palla (Trascuriamo la resistenza dell’aria)
L’accelerazione è costante (gravità)
Scegliere l’asse y verso l’alto: ay = -g
Scegliere l’asse x lungo la terra nella direzione del lancio
Pg 5
Moto del proiettile
Consideriamo una particella che si muove in due dimensioni,
in caduta libera, con velocità v0 e accelerazione di gravità g
costante diretta verso il basso. Alle particelle in queste
condizioni viene dato il nome di proiettile.
Questo è il percorso
che il proiettile segue
y
in condizioni ideali
essendo lanciato con
velocità iniziale v0 che
si può esprimere
come :vo=voxi+ voyj e
conoscendo l’angolo
vox
q si ha: vox=vocosq e
v0
voy=vosenq
q v0y
R
x
Pg 6
Moto del proiettile
Analizziamo il moto del proiettile orizzontalmente e verticalmente.
MOTO ORIZZONTALE
ax =cost
vx=v0x
x-x0=v0xt=(v0cosq)t (1)
MOTO VERTICALE
Il moto verticale è quello di una particella in caduta libera con
a= -g = cost e la variabile spaziale è y. Si ha.
y-y0=v0xt-1/2(gt2)=(vosenq)t – ½(gt2)
vy=vo senq – gt
e
(2)
vy2=(vo senq)2-2g(y-y0)
Pg 7
Diagrammma del Moto Proiettile
Pg 8
Possiamo trovare la traiettoria eliminando la variabile t fra le
equazioni (1) e (2). Sostituendo nella (2) l’espressione di t ricavata
dalla (1) si ha:
t= (x-x0)/vo cosq
x0)/v0cosq]2
y-yo=v0senq [(x-x0)/v0cosq]-1/2g [(x-
Da cui: y=y0+(x-x0)tanq -g (x-x0)2/[v0cosq]2 se y0=0 e x0=0
y= x tanq -g x2/[v0cosq]2
Questa è l’equazione della traiettoria percorsa dal proiettile e
poiché v0, q, e g sono delle costanti, l’equazione ha la forma
y=ax+bx2 che è l’equazione di una parabola e quindi il percorso è
parabolico.
Pg 9
La gittata R del proiettile è la distanza orizzontale massima coperta dal
proiettile all’istante in cui ripassa alla quota di lancio. Per ricavarla
abbiamo x – x0=R e y- y0=0 sempre nelle eq. (1) e (2) e si ha:
R=v0cosqt
e
0= v0senqt – gt2/2
Eliminando la variabile t in queste due eq. si ha:
t = R/v0cosq e quindi R= 2v02senqcosq/g e ricordando che
sen2q=2senqcosq si ottiene :
R=v02sen2q/g
Questa equazione è valida solo quando la quota finale è uguale alla
quota di lancio.
La gittata è massima per sen2q=1 cioè per 2q=90° ossia q=45°
L’angolo q prende il nome di alzo.
Pg 10
Ricapitolazione
Cinematica 2-D, 3-D : Moto del Proiettile
Independenza delle componenti x e y
Pg 11