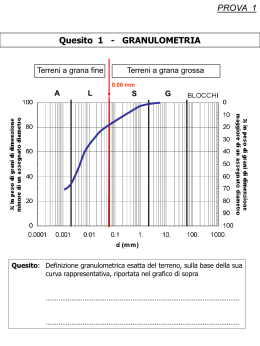
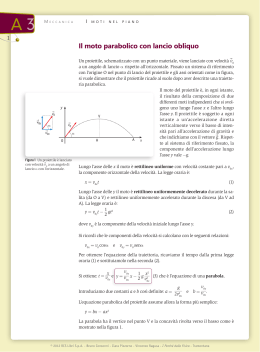
Esempio 1
Un bombardiere vola con velocità orizzontale vx costante di 400 km/h ad una altezza di
3000 m dirigendosi verso un punto che si trova esattamente sulla verticale del suo bersaglio.
Quesito: a quale angolo di vista ф deve essere sganciato il proiettile per colpire il bersaglio ?
Definiamo il quesito in un sistema di assi cartesiani di riferimento
x-y
y
3000 m
vx
x
1
Quello che ci aspettiamo è una cosa del genere,
y
3000 m
ф
x
e siamo interessati alla determinazionedell’angolo di vista ф al quale deve essere
sganciato il proiettile
2
La velocità iniziale v0 del proiettile al momento in cui viene sganciato avrà le seguenti
componenti:
v0x = 400 km/h =
v0y
111 m/s
=0
Il tempo t di caduta del proiettile è connesso all’altezza della caduta y dall’equazione:
y = v0y t – ½ g t2
Da cui
dove
v0y= 0
e
y=
−3000 m
t = (−2y/g)1/2  (−2(−3000) m /
La distanza orizzontale
x = v0x t =
111
9,8
m/s2)1/2 = 24,8 s
x percorsa dal proiettile durante questo tempo t sarà:
m/s x
L’angolo sarà ф = arctan
24,8
s = 2750 m
(x/y) = arctan (2750/3000) = 42,5°
3
Esempio 2
Un giocatore di calcio colpisce una palla ad un angolo di 30° con l’orizzontale,
imprimendo una velocità iniziale di 20 m/s.
4
Per rispondere ai quesiti, supporremo che il moto della palla avviene in un piano verticale.
y
v0 = 20 m/s
Ф = 30°
x
5
1° Quesito: Trovare l’istante t in cui la palla raggiunge il punto più alto della sua traiettoria
Nel punto più alto, la componente verticale della velocità (vy) è zero. Scriveremo quindi:
vy = v0 sin Ф − gt
 v0 sin Ф − gt = 0
Da cui ricaveremo:
t = v0 sin Ф / g
dove: Ф = 30° v0 = 20
t = [20 x ½] m/s / 9,8 m/s2 =
1,02
m/s
g = 9,8 m/s2
s
6
2° Quesito: Qual è l’altezza massima ym raggiunta dalla palla ?
Scriveremo:
y = (v0 sin Ф) t − ½ gt2
L’altezza massima si raggiunge a
Quindi :
t = 1,02 s
ym = ([20 x ½] m/s) x 1,02 s) − 1/2 (9,8 m/s2) x (1,02 s)2
= 5,1 m
7
3° Quesito: Qual è lo spostamento orizzontale della palla e per quanto tempo rimane in aria ?
Scriviamo nuovamente l’equazione per la componente verticale del moto:
y = (v0 sin Ф) t − ½ gt2
Riflettiamo sul fatto che lo spostamento in orizzontale richiesto si raggiunge quando la palla
raggiunge una quota y uguale a quella iniziale e cioè y = 0 . La formula pertanto si riduce a:
(v0 sin Ф) t − ½ gt2 = 0  (v0 sin Ф) t = ½ gt2
(v0 sin Ф) = ½ gt
t = 2 (v0 sin Ф) / g
t = (40 m/s x ½ ) / 9,8 m/s2 = 2,04 s
Per lo spostamento orizzontale scriveremo:
x = v x t = (v0 cos ф) t =
20
m/s x ½ √(3) x
2,04
=
35
m
8
4° Quesito: Qual è la velocità della palla quando tocca terra ?
In sostanza, per definire il vettore velocità in questione dobbiamo ricavare le
sue componenti
vx
e
vy
per le quali potremo scrivere:
vx = (v0 cos ф) t
vy = v0 sin ф − gt
Dove:
t = 2,04 s,
e quindi:
vx = (v0 cos ф) t =
20
m/s x ½ √(3) =
17,3
m/s
vy = v0 sin ф − gt = 20 m/s x ½ − ( 9,8 m/s2 ) x 2,04 s = −10 m/s
v = (v2x + v2y)½ =
20
m/s
ф = arctan (vx / vy) = arctan (−10/17,3) = −30°
9
Risultato prevedibile in base a semplici considerazioni di simmetria .
y
v = 20 m/s
Ф = 30°
v = 20 m/s
Ф = 30°
Ф = -30°
x
10
Esempio 3
Un cannone viene puntato verso un bersaglio posto ad una altezza h che, attraverso un
semplice meccanismo, viene abbandonato in caduta libera esattamente quando il
proiettile lascia la bocca del cannone.
Si osserva che: qualunque sia la velocità iniziale del proiettile, esso colpisce sempre il
bersaglio.
11
12
13
14
Spiegare il fenomeno.
15
Come spiegare il fenomeno ?
Faremo le seguenti considerazioni: se non intervenisse
l’accelerazione dovuta alla gravità:
a) Il bersaglio non cadrebbe
b) Il proiettile si muoverebbe in linea
retta verso il bersaglio
16
In un dato tempo t, il proiettile cade verso il basso
di una distanza −½ gt2 dalla posizione che
avrebbe avuto lungo la linea retta di volo
−½ gt2
Nello stesso intervallo di tempo, il bersaglio cade
della medesima distanza −½ gt2 lungo la verticale
Quindi quando il proiettile incrocia la traiettoria di caduta
del bersaglio, se lo trova esattamente davanti !!!
17
Esempio 4
La luna gira intorno alla terra facendo un giro completo in 27,3 giorni. Si assuma
che l’orbita sia circolare e che abbia un raggio di 385.000 km. Qual è il modulo
dell’accelerazione della luna verso la terra ?
Trasformiamo prima i dati in Unità SI:
r = 385.000 km = 385 x 106 m
Il periodo T di rivoluzione è:
T=
27,3 giorni = 23,6 x 105 s
La velocità della luna (in modulo) che supporremo costante é:
v = 2πr / T = 1020 m /s
L’accelerazione centripeta è pertanto: a
= v2/r
Ovvero: 2,8 x 10-4 g
= 0,00273 m/s2
18
Esempio 5
Si consideri un satellite artificiale che ruota attorno alla terra e si supponga per
semplicità che esso viaggi proprio sopra la superfice terrestre.
Quesito: Si calcoli il modulo della velocità del satellite, assumendo un raggio della terra
R = 6.000 km
Sulla superfice terrestre l’accelerazione di gravità vale: g
= -9,8 m/s2
ed è questa
l’accelerazione che fa muovere il satellite di moto circolare, è cioè la sua accelerazione
centripeta. Da cui
a = v2/R

v = (a R)1/2 = 7668 m/s = 27.5 km/h 19
Esempio 6
La bussola di un aeroplano indica che si sta dirigendo verso est. Si registra un forte
vento che soffia in direzione nord.
1° Quesito: Mostrare su di un diagramma la velocità dell’aeroplano rispetto al suolo.
Nord
v
y
u
α
Est
v’
u = vettore della velocità dell’aria rispetto al suolo
v’ = vettore della velocità dell’aeroplano rispetto all’aria
v = vettore della velocità dell’aeroplano rispetto al suolo
x
(punta verso nord)
(punta verso est)
( = v’ +
u da determinare)
20
Risulta evidente che:
vx =
vy =
modulo (v’) = v’
modulo (u) = u
α = arctan (vy / vx) = arctan(u / v’)
Il modulo della velocità v dell’aeroplano rispetto al suolo sarà:
v = ((v’)2 + u2)1/2
Così, per esempio, se l’aeroplano si muove rispetto all’aria di 300 km/h e la
velocità del vento rispetto al suolo è di 60 km/h si avrà:
v=
(3002 + 602)1/2 = 306 km/h
α = arctan (60/ 300)
= 11° 20’
21