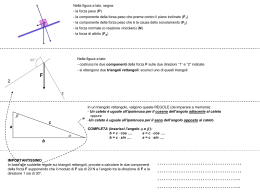
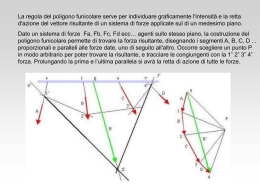
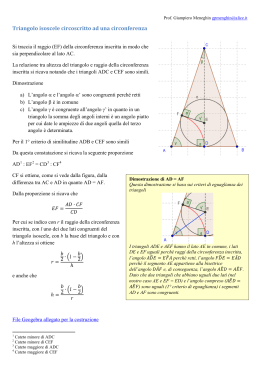
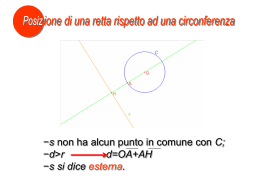
In un triangolo ABC un angolo esterno è
maggiore di ciascun angolo interno ad
esso non adiacente.
>
A


B

C
ed
>
1
A
Consideriamo il punto medio M
del lato AC.

.
M

Quindi AM = MC.
B

C
D
A
Tracciamo il segmento MB e lo
prolunghiamo dalla parte di M
di MD uguale ad MB.


B
.
M

C
2
Unendo D con C vengono a
formarsi i triangoli AMB e
CMD.
D
A
AMB


.
B

C
Questi due triangoli hanno:
D
A

AMˆ B  DMˆ C perché opposti al vertice
BM = DM, per costruzione
CMD
M

B
.
M

C
AM = MC, perché M è punto medio di AC.
3
Pertanto l’angolo BAM è uguale all’angolo DCM.
D
A


B
.
M


C
Essendo l’angolo DCM minore di  segue che
BAM  
c.v.d.
4