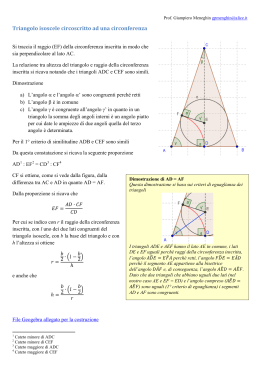
−s non ha alcun punto in comune con C;
−d>r
d=OA+AH
−s si dice esterna.
−s ha un punto in comune con C;
−d=r
d=OA
−s si di tangente.
−s ha due punti in comune con C;
−d<r
d=OH;
−s si dice secante.
−C’ non ha alcun punto in comune con C;
−d>r+r’
d=OA+AA’+A’O’;
−C e C’ si dicono esterne.
−C’ ha un punto in comune con C;
−d=r+r’
d=OA+A’O’;
−C e C’ si dicono tangenti esterne.
−C’ ha due punti in comune con C;
−d<r+r’;
−C e C’ si dicono secanti.
−C’ ha un punto in comune con C;
−d=r-r’
d=OA-AO’
−C e C’ si dicono tangenti interne.
−C’ non ha alcun punto in comune con C;
−d<r-r’;
−C’ e C si dicono una interna all’altra.
− L’angolo al centro AÔB insiste sull’arco AB;
− L’angolo al centro corrisponde all’arco AB;
− Ad ogni angolo al centro corrisponde un solo arco
e viceversa
^
− L’angolo alla circonferenza AVB insiste sull’arco
AB;
− Ogni angolo alla circonferenza individua un solo
arco sul quale insiste;
− Ad uno stesso arco corrisponde un numero
infinito di angoli alla circonferenza.
Un angolo al centro e uno alla circonferenza che
insistono sullo stesso arco si dicono corrispondenti.
OGNI ANGOLO ALLA CIRCONFERENZA È LA
METÀ
DELL’ANGOLO
AL
CENTRO
CORRISPONDENTE.