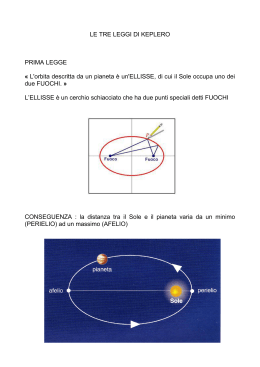
Il telegrafo ottico di Polibio (circa 203–120 a.C.)
La linea dei fuochi tra Gondor e Rohan
7 fuochi per coprire 150 miglia
Johannes Kepler (1571-1630)
Pubblica tre opere astronomiche
1) Mysterium Cosmographicum, Tubinga, 1597
2) Astronomia Nova, Praga 1609 (I e II legge)
3) Armonice Mundi Libri V, 1618 (III legge)
I Legge: Le orbite descritte dai pianeti sono ellissi di cui il Sole occupa uno dei fuochi
(conservazione del momento della quantità di moto –la forza di gravità è centrale–).
II Legge: Le aree descritte dal raggio vettore che va dal Sole a un pianeta sono
proporzionali ai tempi impiegati a descriverle (“spazzarle”).
III Legge: Il periodo di rivoluzione di un pianeta è proporzionale al semiasse maggiore
elevato a 3/2.
1. Mysterium Cosmographicum, 1597
Prodromo ai trattati cosmografici, contenente il mistero cosmico delle ammirevoli
proporzioni delle orbite celesti e le vere e giuste ragioni del loro numero, grandezza e
movimento periodico.
Il Sole è al centro dell’universo «per ragioni fisiche e metafisiche» e sei pianeti gli
girano attorno con orbite circolari.
Ricordando Platone, Keplero afferma che le posizioni dei pianeti sono determinate dal
fatto che essi sono iscritti e circoscritti ai 5 solidi regolari: tetraedro, cubo, ottaedro,
dodecaedro e icosaedro. Le distanze tra i pianeti risultano quindi regolate da precisi
rapporti matematici.
Saturno è il pianeta più esterno, al quale è inscritto un cubo. Inscritto al cubo vi è
Giove a cui analogamente succedono il tetraedro, Marte, il dodecaedro, la Terra,
l’icosaedro, Venere, l’ottaedro e infine Mercurio.
Keplero in seguito abbandonerà questa teoria, decisamente inconciliabile con i dati delle
osservazioni astronomiche precise di Tycho Brahe.
Esempi di argomentazioni di keplero
«Persi quasi tutta l’estate in questo grosso lavoro. Alla fine mi avvicinai
alla verità in un frangente di minima importanza. Credo che la Provvidenza
divina sistemò le cose in modo da farmi ottenere per caso quello che i miei
sforzi non mi avevano consentito di raggiungere; ne sono tanto più
convinto che ho sempre pregato Dio per la buona riuscita del mio piano se
Copernico ha detto il vero.»
«Allora mi spinsi più avanti. Perché volere che figure a due dimensioni si
adattino alle orbite nello spazio? Bisogna ricercare forme a tre dimensioni
e vedi, caro lettore, adesso tu hai in mano la mia scoperta. »
Tenta di trovare una legge matematica che lega i rapporti tra distanza e periodo,
ma non la trova (la troverà, per caso, nel 1619, III legge di Keplero):
«Avrei dovuto prevederlo al momento di cominciare. Tuttavia non ho voluto
nascondere al lettore ciò che può incoraggiare a nuovi sforzi. Ah! Potessimo
vedere il giorno in cui le due serie di numeri si accordano…Ho soltanto voluto
che altri si sentano stimolati a ricercare la soluzione di cui ho tracciato la via. »
Nella primavera del 1597 ne invia delle copie a Galileo (mai incontrato, Galileo
non risponderà mai) e a Tycho Brahe.
Galileo respinge le speculazioni mistiche e tutto il libro, è prevenuto fin
dall’inizio contro Keplero.
Tycho è interessato. Nel 1601 Keplero andrà a Praga dove è già Tycho da
qualche anno, vi rimane fino al 1612, morte dell’Imperatore Rodolfo II protettore
di Tycho e di Keplero.
2. Astronomia Nova, Praga 1609
Nuova Astronomia Causativa ovvero Fisica Celeste, tratta dai commentari Dei
Movimenti di Marte sulla base delle osservazioni di G.V. Tycho Brahe.
Distinzione tra Fisica e Astronomia e “invasione di campo”.
Vi lavora senza interruzione dal 1600 al 1609. Contiene la I e la II legge di Keplero. Una
marea di conti!
Marte ha un’orbita particolarmente ellittica: nessun cerchio si accordava con le misure di
Tycho Brahe. Tycho affida all’ultimo arrivato (Keplero) il problema.
8 minuti di grado di scarto! Ossia 8/60 di grado.
La Luna e il Sole si vedono sotto 0,5°, ossia 30/60°. I dati di Tycho erano più precisi di
quelli di Tolomeo e di Copernico. Questi 8 minuti sono la dannazione di Keplero.
Koestler ricorda (I sonnambuli): attraverso tre metodi sbagliati, difesi in modo ancor più
sbagliato, capitò sulla legge giusta.
Keplero sulle orbite:
«La conclusione è semplicemente che il tragitto di un pianeta non è un cerchio, si
incurva da due parti e si estende alle altre estremità. Queste curva si chiama ovale.
L’orbita non è un cerchio, bensì una figura ovale. »
Il 4 luglio 1603 scrive a un amico che non riusciva a risolvere i problemi geometrici del
suo uovo; ma «se soltanto la forma fosse un’ellisse perfetta, si troverebbero tutte le
risposte in Archimede e in Apollonio.»
Diciotto mesi dopo scriveva allo stesso corrispondente che la verità doveva trovarsi a
metà strada tra l’ovale e il cerchio «esattamente come se l’orbita di Marte fosse
un’ellisse perfetta. Ma a questo riguardo non ho ancora esplorato nulla.»
La cosa più stupefacente è che usava costantemente l’ellisse nei suoi calcoli, però
unicamente quale mezzo per determinare, per approssimazione, l’area del suo ovale.
Rifà altri calcoli e arriva a trovare un altro ovale, simile a un cerchio appiattito da
due lati e che di conseguenza formava due strette falci tra il cerchio e tale orbita.
L’ampiezza della falce nel punto più spesso equivaleva a 0,00429 del raggio.
«Mi chiesi perché e come si producesse una falce esattamente di quello spessore
(0,00429). Questo pensiero mi tormentava e pensavo di continuo…che la mia
apparente vittoria su Marte era stata vana [aveva trovato un altro ovale], quando
per puro caso caddi sulla secante dell’angolo 5° 18’, che è la misura della più
grande equazione ottica. Quando vidi che questa secante è uguale a 0,00429, mi
sembrò di risvegliarmi…»
0.00429 a = a − b
In termini moderni
a 2 − b2 = c2
Ma c = ae dove e è l’eccentricità (per Marte, e = 0.093)
Quindi, Keplero troverebbe e = 1 − (1 − 0.0049) = 0.0989 (con i dati di Tycho)
2
Dimenticò il risultato per costruire geometricamente un’ellisse e scoprì che i due metodi
davano lo stesso risultato.
«Perché non parlare fuori dai denti? La verità della natura che avevo respinto e cacciato,
tornò quatta quatta per la porticina mascherandosi per farsi accettare. Cioè misi da parte
[l’equazione ricavata dalla secante] e ricaddi sulle ellissi, credendo si trattasse di
un’ipotesi diversa, mentre le due ipotesi, come dimostrerò nel prossimo capitolo, sono
un’unica e identica cosa…Ho rischiato di impazzire a cercare una ragione che spiegasse
perché il pianeta preferiva un’orbita ellittica…Ah! Come sono stato stupido!»
3. Armonice Mundi Libri V, 1618
I cinque libri della scienza dell’armonia del mondo
È l’espressione di un progetto universale, con il quale Keplero intende mostrare come le
leggi dell’armonia si possano scorgere in ogni aspetto del creato.
Lungo lo svolgersi dei cinque Libri si ritrovano le stesse relazioni armoniche, applicate
di volta in volta alla geometria, alla politica, alla musica, all’astronomia o
all’astrologia.
Secondo alcuni storici, keplero scoprì quasi per caso la III Legge, e la inserì poi nel libro
dedicato alla musica.
Molti contemporanei di Keplero, che pure erano più abituati a trattazioni in cui la
scienza era profondamente impregnata di filosofia, politica, teologia e studi astrologici,
non si accorsero affatto della presenza della III Legge. Persino Newton ne sottovalutò
l’importanza introducendo la III Legge anonimamente.
(Anna Maria Lombardi, Keplero, Codice Edizioni,2008)
Intervallo convergente: confronta la velocità minima del pianeta interno con la velocità massima di quello
esterno. Intervallo divergente confronta la velocità massima del pianeta interno con la velocità minima di
quello esterno.
Dalla tabella emerge come tutti i rapporti coincidano in buona approssimazione
con intervalli musicali, tranne quelli relativi alla coppia Marte-Giove, la cui
dissonanza è motivata da una «incompatibilità astrale» tra i due pianeti.
L’esponente 3/2 della III Legge, coincide con il rapporto su cui era costruita la
scala musicale pitagorica.
La musica celeste è puramente razionale, non sonora.
Nel terzo capitolo del Libro V, Keplero racconta che già l’8 marzo
del 1618 aveva scritto la legge esatta, ma l’aveva scartata credendola
imprecisa: semplicemente aveva sbagliato i calcoli. Ma il 15 maggio
l’idea si era ripresentata e finalmente «l’ebbe vinta sulle tenebre della
mia mente»
Negli ultimi capitoli del Libro V riporta le conferme sperimentali
ottenute usando i dati di Tycho.
Con i nuovi rapporti tra velocità minime e massime ricalcola
eccentricità e velocità medie e, sfruttando la III Legge, le distanze
medie dei pianeti dal Sole. Organizza i risultati in una tabella.
L’Avviso Astronomico di Galileo (1610) (Sidereus Nuncius)
Il Sidereus Nuncius, ossia l’Avviso Astronomico, è il resoconto scientifico
delle osservazioni celesti di Galileo, in particolare della sua scoperta dei satelliti
di Giove.
Scritto a Padova nel gennaio-febbraio 1610 in latino, data la sua destinazione
accademica ed europea, fu stampato a Venezia il 13 marzo dello stesso anno, in
550 copie, esaurite dopo una settimana.
L’opera, preceduta da una dedica a Cosimo II de’ Medici, pur senza essere
suddivisa in capitoli, presenta una scansione rigorosa e moderna, che vede nella
scoperta dei pianeti Medicei l’ultimo e principale argomento.
L’immediato successo dell’opera dette a Galileo, prima conosciuto da pochi,
fama internazionale ben oltre i limiti della comunità scientifica, all’età di circa
46 anni.
Il “libretto” si leggeva in 2 ore ed era subito comprensibile! Galileo era
rivoluzionario anche nella scelta dello stile, nella scrittura limpida e concreta,
facile da leggere, sobria e asciutta.
Con una lingua spoglia, sobria ed efficace, Galileo inaugura un nuovo genere
letterario, il breve scritto scientifico, un articolo lungo per gli standard moderni.
Scritto e stampato con urgenza subito dopo le scoperte, questo testo supera, per
stile, efficacia e modernità d’esposizione tutte le altre pubblicazioni dell’epoca.
Anticipa il nuovo mezzo di comunicazione, il breve articolo scientifico
pubblicato nelle riviste della seconda metà del secolo XVII.
L’organizzazione è molto simile alla moderna struttura canonica. Può essere
considerato la prima pubblicazione scientifica moderna.
Il trattato uscì in una forma dimessa per l’importanza della materia, scritto di
fretta durante il giorno, mentre di notte continuavano senza posa le osservazioni,
fornito a rate allo stampatore, senza neppure rivelare, nelle parti iniziali dello
scritto, la posizione dei quattro nuovi pianeti per evitare “fughe” di notizie.
Dal 15 gennaio 1610 i suoi appunti sono scritti in latino perché evidentemente
aveva deciso di pubblicare i risultati.
La sua bravura nel disegno e nella tecnica dell’acquerello gli evitò anche di
rivolgersi a dei pittori, altra possibile fonte di fughe di notizie.
Alla veste editoriale povera corrispondeva una prosa nella lingua internazionale
dell’epoca, il latino che, per quanto padroneggiato da Galileo, era scolastico, non
aveva l’eleganza arguta ed espressiva della sua inimitabile prosa italiana.
A qualcuno lo stile parve addirittura arido (oggi ci appare moderno),
osservazione corretta, specie se il lettore era Keplero, scienziato dotato di una
profonda cultura umanistica e grande virtuoso della lingua latina.
La fretta di battere tutti sul tempo era prevalsa sul desiderio di stampare un’opera
adeguata alla grandezza e all’importanza del soggetto, perché Galileo sapeva
che la tecnologia necessaria per costruire un cannocchiale come il suo poteva
essere sviluppata in poco tempo.
Per questo motivo, e anche perché doveva mantenere il segreto, per ordine della
Repubblica di Venezia, Galileo evita accuratamente di fornire informazioni
tecniche utili per costruire un cannocchiale adeguato, ad esempio come molare le
lenti, tanto da monopolizzare per alcuni anni la ricerca astronomica.
Nonostante le insistenze di amici e discepoli, che gli chiedevano una versione
riveduta e migliorata nello stile (retorico !), Galileo non scrisse mai una seconda
edizione, perché impegnato in molte altre faccende (e dispute).
Titolo completo
Avviso Astronomico che palesa spettacoli grandi e straordinariamente
meravigliosi e li propone alla contemplazione di tutti e in particolare dei
filosofi e degli astronomi, spettacoli che da Galileo Galilei patrizio
fiorentino, pubblico matematico nel Ginnasio Patavino, per mezzo
dell’occhiale perfezionato da lui stesso ritrovato in questi ultimi tempi,
sono stati osservati sulla superficie della Luna, in una quantità
innumerevole di stelle fisse, nella Via Lattea, nelle nebulose, e soprattutto
in quattro pianeti, che con sorprendente velocità ruotano intorno all’astro
Giove a diverse distanze e in differenti periodi; e questi, che nessuno fino
ad ora conobbe, l’Autore li scorse per primo recentissimamente e decise di
chiamarli Astri Medicei
Cosmici è corretto in Medicei
Il cannocchiale
La Luna
«Le elevazioni lunari son più alte delle terrestri»
Le nebulose
I quattro pianeti Medicei
La doppia elica (1953)
James Dewey Watson (1928)
Francis Harry Compton Crick (1916-2004)
1)
Titolo
2)
Introduzione (paragrafi 1-3)
3)
Corpo (paragrafi 4-10)
4)
Conclusioni (paragrafi 11-13)
5)
Ringraziamenti (paragrafo 14)
«It has not escaped our notice that the specific pairing we have
postulated immediately suggests a possible copying mechanism
for the genetic material.»
Figura retorica nota come litòte, che nega il contrario del
concetto che si vuole affermare.
Crick F., La folle caccia. La vera
storia della scoperta del codice
genetico. Milano, Rizzoli, 1990.
Scrittura e creatività
Scrivere un articolo non è un esercizio di ricostruzione fedele del processo creativo,
ma ne fa parte.
Percorso tortuoso e in salita che l’autore ha seguito per arrivare alle
conclusioni, e percorso diritto e in discesa che il lettore vuole percorrere.