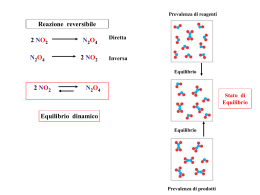
REVERSIBILITA’ DELLE REAZIONI
ED EQUILIBRI CHIMICI
Solubilizzazione del carbonato di calcio in ambiente acido
CaCO3 (s) + CO2 (aq) + H2O (l)  Ca2+ (aq) + 2HCO3- (aq)
CaCO3
Ca2+ (aq) + 2HCO3- (aq)  CaCO3 (s) + CO2 (g) + H2O (l)
Precipitazione del carbonato di calcio
Data la reazione generica:
A+B C
concentrazione
Seguendo nel tempo le variazioni di concentrazione
dei reagenti e prodotti, osseviamo:
Regione di
equilibrio
Regione
cinetica
tempo
tetrossido d’azoto
2 NO2
N 2O 4
concentrazione
concentrazione
biossido d’azoto
NO2
N 2 O4
NO2
tempo
N.B.
N 2 O4
tempo
indipendentemente dal fatto che si parta dal 100% di reagente
(NO2) o dal 100% del prodotto N2O4 all’equilibrio avremo sempre
lo stesso rapporto di concentrazioni.
L’equilibrio chimico è una condizione dinamica
Situazione iniziale
Situazione all’equilibrio
NO2
N2O4
NO2
Statisticamente avremo
2 molecole di NO2 e 4 di N2O4
LEGGE DELLE AZIONI DI MASSA (SISTEMI CHIUSI)
aA + bB
cC + dD
[C]c [D]d
Costante di equilibrio = K =
[A]a [B]b
Esempio:
H2 (g) + I2 (g)
2 HI (g)
H2 (g)
I2 (g)
HI (g)
Concentrazioni iniziali
0.0175
0.0175
0
Variazioni delle
concentrazioni nel
raggiungimento dell’equilibrio
-0.0138
-0.0138
+0.0276
Concentrazioni all’equilibrio
0.0037
0.0037
0.0276
[ HI]2
[H2][I2]
=
(0.0276)2
=
(0.0037)(0.0037)
56
Principio di Le Chatelier
Se un sistema all’equilibrio subisce una
alterazione il sistema reagirà in modo da
annullare, almeno in parte, l’alterazione subita.
• Modificazione della concentrazione di un
reagente o di un prodotto
• Modificazione della temperatura
• Modificazione della pressione o del volume
Principio di Le Chatelier
• Modificazione della concentrazione di un reagente o di un prodotto
Consideriamo la generica reazione : A + B  C
partendo con 20A e 20B si perviene all’equilibrio: 10 A + 10 B
[C]
K=
_______
[A] [B]
10 C
[10]
=
__________ =
0.1
[10] [10]
Immaginiamo di aggiungere 5 C alla miscela in equilibrio
10 A + 10 B
10 C
Quello che accade è che delle 5 molecole di C 2 vengono convertite in 2 A e 2B
generando il nuovo equilibrio:
12 A + 12 B
13 C
[13]
K=
__________
[12] [12]
 0.1
I2 + H2
2 HI
Partendo dal sistema all’equilibrio:
Se aggiungiamo un extra quantità di
I2 il sistema reagirà aggiustando le
concentrazioni delle specie chimiche
ristabilendo un nuovo equilibrio con
la stessa Ke
- H2
+ I2
I2 + H2
Se rimuoviamo un po’ di H2 ,di nuovo,
il sistema reagirà aggiustando le
concentrazioni delle specie chimiche
ristabilendo un nuovo equilibrio con
la stessa Ke
2 HI
I2 + H2
2 HI
Esempio – trasporto dell’O2 nel sangue
equilibrio
Il trasporto dell’ossigeno da parte dell’emoglobina è un
esempio di adattamento continuo dell’equilibrio alle
differenti condizioni ambientali
Nei polmoni vi è abbondanza di ossigeno quindi:
L’equilibrio è spostato a destra e l’ossigeno è legato
all’emoglobina
Quando il sangue raggiunge le cellule, dove vi è carenza
di ossigeno:
L’equilibrio si sposta a sinistra, e l’ossigeno viene
rilasciato dall’emoglobina
Se ad esempio:
Il rapporto della forma
ossigenata rispetto alla
deossigenata è:
Se la solubilità dell’O2 nel sangue a 37°C= 0.1 M :
nei polmoni
Nei capillari, il livello di O2 è circa 0.001M e quindi:
Dipendenza dell’equilibrio dalla temperatura:
•Se una reazione è esotermica un aumento della
temperatura sposta a sinistra (verso i reagenti)
l’equilibrio e la Ke diminuisce.
•Se la reazione è endotermica un aumento della
temperatura sposta a destra (verso i prodotti)
l’equilibrio e la Ke aumenta.
Tale comportamento comune alla maggior parte delle
reazioni può essere spiegato immaginando il calore
come una specie di reagente.
A + cal
A
B
B + cal
Reazione
endotermica
Reazione
esotermica
+ cal
A + cal
A
B
+ cal
B + cal
Data una reazione generica
aA + bB
cC + dD
il quoziente di reazione è definito dall’equazione
[ C ] c [ D ]d
Q=
[ A ]a [ B ] b
N.B.
L’espressione matematica di Q ha l’aspetto di
una espressione di equilibrio ma differisce da
Keq perché le concentrazioni che vi compaiono
non sono necessariamente le concentrazioni
all’equilibrio
A
B
B
A
A B B
A
4A
4B
A
A
A
4A
B
B
A B B
4B
C
D D
C C
D
D D
C C
D
C
D
C
C D
8C
Keq=
8D
C
D D
C C
D
D D
C C
D
C
D
C
C D
8C
A+B
C + D
8D
Non accade niente
[C][B]
[A][B]
=
(8)(8)
(4)(4)
=4
C
D
C
D
D
D D
D B
C
C
A
C A
B
A
C
C
D C B D
A
4A
B
4B
8C
8D
concentrazioni di
reagenti e prodotti non
all’equilibrio
[C][B] (10)(10)
Q =
=
= 25
[A][B]
(2)(2)
quoziente di reazione
A
B
B
A
2A
A
A
2A
2B
B
B
2B
C C D DD
C C
D
D D
C C
C C
D
D
C
C D D
10 C 10 D
C C D DD
C C
D
D D
C C
C C
D
D
C
C D D
10 C 10 D
C
D
C
D
D
D D
D B
C
C
A
C A
B
A
C
C
D C B D
A
4A
B
4B
[C][B]
[A][B]
=
8C
(8)(8)
(4)(4)
8D
= 4 = Keq
concentrazioni di
reagenti e prodotti non
all’equilibrio
[C][B] (6)(6)
Q =
=
=1
[A][B]
(6)(6)
quoziente di reazione
A
B
A A
A
A
A
B B
B B
B
6A
6B
A
A A
A
A
A
6A
B
B B
B B
B
6B
C
C
C C
C
C
6C
C
C C
C
C
C
6C
D D
D
D
D
D
6D
D D
D
D
D D
6D
C
D
C
D
D
D D
D B
C
C
A
C A
B
A
C C
D C B D
A
4A
[C][B]
[A][B]
B
4B
=
8C
(8)(8)
(4)(4)
8D
= 4 = Keq
Relazione tra quoziente di reazione e
costante di equilibrio
1. Se Q < K, il sistema non è all’equilibrio e
avviene la reazione Reagenti  Prodotti
2. Se Q = K, il sistema è all’equilibrio
3. Se Q > K, il sistema non è all’equilibrio e
avviene la reazione Prodotti  Reagenti
VARIAZIONE DI ENERGIA LIBERA NEL CORSO DI UNA REAZIONE
Energia libera G
A+B
A+B
C+D
GREAGENTI = GA + GB
DG = GPRODOTTI – G REGENTI
GPRODOTTI = GC + GD
100%
reagenti
Coordinate di reazione
C+D
100%
prodotti
GX = G°X + R T ln[X]
R = costante universale dei gas = 8.314 J/(mol.K)
T = temperatura assoluta= 273.15 + °C
quando [X] = 1  GX = G°X
G° = energia libera in condizioni standard
Condizioni standard
pressione= 1 atmosfera
temperatura = 25 °C
concentrazione unitaria
1 M per soluzioni
1 per sostanze allo stato liquido o solido
N.B.
l’importanza della equazione è che ci permette di calcolare la
l’energia libera di una sostanza in condizioni non standard
(attuali)
Energia libera G
A+B
GREAGENTI = GA + GB
DG = GPRODOTTI – G REGENTI
GPRODOTTI = GC + GD
100%
reagenti
Considerando che
GX = G°X + R T ln[X] 
Coordinate di reazione
C+D
100%
prodotti
DG = DG° + RT ln([C]c[D]d) / ([A]aB]b)
La variazione DG rappresenta la variazione di energia libera in funzione
delle concentrazioni attuali dei reagenti e prodotti
DG = DG° + RT ln([C]c[D]d) / ([A]aB]b)
se ([C]c[D]d) / ([A]aB]b) = Q
DG = DG° + RT ln Q
quando [A]; [B]; [C]; [D] = 1  ln 1 =0
DG = DG°
variazione di energia libera in condizioni standard,
cioè quando reagenti a concentrazione di 1 M
vengono convertiti completamente in prodotti.
quando il sistema è all’equilibrio  ([C]c[D]d) / ([A]aB]b) = Keq
non produce trasformazioni nette spontanee e quindi
DG = 0 = DG° + RT ln K 
- DG° = RT ln K
da cui
K = e –DG°/RT
quindi noto il DG°RXN standard è possibile calcolare la Keq
Andamento di come variano i parametri termodinamici
(energia libera, entalpia, entropia) trasformano reagenti in prodotti,
per la reazione generica R -> P
condizione di
equilibrio
Relazione tra DG° e Keq
A+B
C+D
La reazione è a favore dei prodotti
DG° < 0, K >1
Energia libera G
A+B
DG° < 0
Q<K
C+D
Q>K
Q=K
100%
reagenti
Sistema
all’equilibrio
Coordinate di reazione
100%
prodotti
A+B
Relazione tra DG° e Keq
C+D
La reazione è a favore dei reagenti
DG° > 0, K <1
Energia libera G
C+D
DG° > 0
Q>K
A+B
Q<K
Q=K
100%
reagenti
Sistema
all’equilibrio
Coordinate di reazione
100%
prodotti
A+B
C+D
DGA+BC+D = DG° + RT ln Q
DG = DG° +2.3 RT log Q
Es.: DG°=10 KJ/mole, R=8.314 J/mol K, T= 273+25°C
DG>O reazione endoergonica
30
DG=0
25
-DG°/2.3RT
Q= Keq= 10
= 0.0177
20
D G (KJ/mole)
15
10
Q=1
D G = D G°= 10 KJ/mol
5
0
1E-04 0,001
0,01
0,1
1
10
-5
-10
-15
-20
DG<O reazione esoergonica Q (scala logaritmica)
100
1000 10000
CH2PO32H
O
OH
H
OH
HO
H
H
OH
Glucoso 6P
[0.665]
CH2PO32O
CH2OH
H
H
OH
HO
DG° = + 1.7 KJ/mol
OH
Fruttoso 6P
[0.335]
Calcolando la Keq:
K= e-DG°/RT = e-1700/(9.314x298) = 0.504 = ([F6P]/[G6P])eq
Essendo K < 1 la reazione prevede un equilibrio spostato a sinistra
Se [F6P] + [G6P] = 1  [F6P] =0.335, [G6P] =0.665
N.B.
Nella realtà biochimichica le [ ] non sono all’equilibrio (la cellula è
un sistema aperto) e le variazioni di energia libera devono essere
espresse in termini di DGattuale
DG = DG° + RT ln Q = 1.7+ RT ln[F6P]/[G6P]
1
0.8
Glucosio 6 P
0.6
0.4
CH2PO32
-
0.2
0
H
H
O
+ 15
Glucoso 6P
H
OH
OH
HO
OH
DG, KJ/mol
H
+ 10
+5
CH2PO32
CH2OH
-
O
Fruttoso 6P
H
0
- 1.72
H
Sistema all’equilibrio
OH
HO
OH
-5
Condizioni in stato-stazionario
intracellulare
- 10
CH2PO32
O
0
0.2
0.4
0.6
Fruttosio 6 P
0.8
1
Fruttoso 1,6bis P
H
H
- 15
CH2PO4
-
HO
OH
OH
Sistema isolato
Tende a raggiungere l’equilibrio
G6P/F6P= 0.5 = Keq
Sistema aperto
Tende a mantenere uno stato stazionario
G6P/F6P= 0.25 = Qstato stazionario