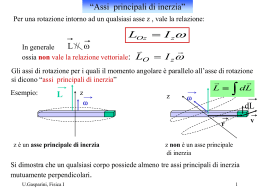
Dinamica dei moti rotatori


F  ma

F
Dinamica del punto
materiale
Asse di rotazione
• a dipende dalla forza e dal
punto in cui viene applicata
(momento di F)
• a dipende dalla distribuzione
rispetto all’asse di rotazione
(momento di inerzia)

a 0

a 0

a 0
1
Momento torcente
FT  Fsen 
F
Agisce sulla rotazione attorno
all’asse z.

L’accelerazione angolare dipenderà
da FT e dalla distanza r.
FR  F cos 
  rFsen
Non ha alcun effetto sulla rotazione
2
Momento torcente
 
  r F


F

[Nm]
  rFsen
3
Esempio momento forza peso
O
L
m
Si determini momento torcente rispetto ad O se
m si trova a destra o sinistra.
4
Momento di inerzia
La massa è una caratteristica univoca di un corpo.
Il momento di inerzia dipende da come è distribuita la massa del
corpo rispetto all’asse di rotazione.
Massa vicino all’asse di
rotazione…minore inerzia
…minore resistenza alla rotazione
Viceversa
massa in media in regioni più lontane
dall’asse di rotazione…maggiore
inerzia …maggiore resistenza alla
rotazione
5
Momento di inerzia di una particella
F// asse di rotazione non ha effetto sul moto
F
T
Fsen  maT 
Fsen  ma z r
rFsen  ma z r 2 
 z  mr a z
2
I  mr
2
Momento di inerzia
 z  Ia z
6
Momento di inerzia di sistema di particelle

F
y
r1 m
 1
T1
Sistema costituito da m1 e m2 libere
di ruotare attorno all’asse z. r1 ,r2 e r
sbarre di massa trascurabile

T1r

T2 r
 m2
T2
r2


T1r  T2 r
x
   
 F1  P  T1 T1r
  
 F2  T2 T2r
Momento torcente
 
z
z1
  z 2   FT 1 r1   FT 2 r2
7
Momento di inerzia di sistema di particelle

z
(m1a1T )r1  (m2 a2T )r2 
 (m1a z r1 )r1  (m2a z r2 )r2  (m r )a z  (m2 r 2 )a z 
2
1 1
2
 (m r  m2 r 2 )a z  Ia z
2
1 1
2
I  m r  m2 r
Momento di inerzia
del sistema
I  m r  m2 r
2
1 1
2
1 1
2
2
n
2
2
 ..   mi r
2
i
i 1
8
Momento di inerzia di sistema di particelle
y

F
r1 m
 1
T1

T1r

T2 r
 m2
r2 T2
x
 z Ia z
Momento delle Forze esterne
Espressione rotazione della II Legge di
Newton.


F  ma
9
Momento di inerzia dei corpi rigidi
n
I   mi r
i 1
2
i
Corpo rigido: distribuzione continua di
massa, suddivisa in infiniti elementi di
massa infinitesima m
n
I  lim  mi r
m 0 i 1
2
i
I   r dm
2
10
Tabella Momenti di inerzia
11