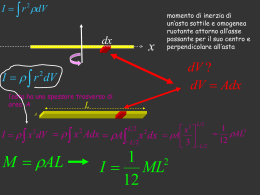
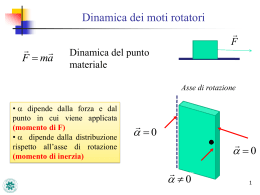
Determinazione analitica del
momento di inerzia
anello sottile,disco,sfera,guscio
sferico,asta sottile rispetto all’asse
di simmetria o ad un asse notevole
Momento di inerzia di un anello sottile, o
uno strato cilindrico omogeneo, di
spessore trascurabile e di raggio R
rispetto al suo ad un asse
perpendicolare alla sezione circolare
dell’anello e passante per il suo
centro
2
dA ?
s
R
l
I   r dm
la
formula
generale
I  MR
2
•simmetria cilindica, coordinate cilindriche
•densità superficiale costante ;
dA  sl
quindi dm = dA
s
d
R
s  Rd
I   R dA  R   dA  R lR 
2
 R l 2R
2
2
M  l 2R
2
2
0
d
proiezione
dello strato
sottile
cilindrico
esempio
1
I   r dV
2
I    r dV
2
dV  2rldr
M
momento di inerzia di un disco
omogeneo di massa M , raggio R e
spessore l che ruota rispetto al
suo asse
dV ?
esempio 2
R
dr r
l
M
il volume “ elementare” di
integrazione è un anello cilindrico, di
altezza l e che ha per base la corona
R
circolare di raggio
r e spessore dr
2
2
R
R
I    r 2rldr  2l  r rdr  2l  r dr
20
4
0
R  lR 2 R
 2l
2
2
4
MR
2
I
M  lR
2
2
3
2
momento di inerzia di una sfera omogenea
z
•
•
•
•
•
si vuol determinare il momento
di inerzia di una sfera
omogenea di massa M e raggio R
rispetto ad un asse passante
per il centro
consideriamo la terna
ortogonale Oxyz della figura,
dove O coincide con il centro
della sfera.
Per ragioni di simmetria il
momento di inerzia rispetto ad
un generico asse passante per 0
concide con quello rispetto
all’asse x, o a quello rispetto
all’asse y o z.
questi momenti di inerzia sono
rispettivamente
sommando membro a membro si
ottiene
y
O
x


I x    y 2  z 2 dV

V
V


I z    x 2  y 2 dV
V


I x  I y  I z  3I  2  x 2  y 2  z 2 dV  2   r 2 dV
V

I y    x 2  z 2 dV
V
3I  2   r 2 dV
z
simmetria
sferica,
coordinate sferiche o
polari
2
2
I    r dV
3 V
V
volume elementare dV lo strato sferico di raggio
r e spessore dr, dove r varia da 0 a R
la superficie dello strato sferico di
raggio r è dato da: 4r 2
da cui si ricava
dV  4r 2 dr
4 3
ricordando che il volume della sfera è
V  r
3
4
e che la massa della sfera
3
M


V


R
omogenea è
3
r
y
x
R
8
I    r 4 dr
3
0
8
R5
I  
3
5
2
5
I  MR
5
momento di inerzia di un guscio sottile sferico
omogeneo, rispetto ad un asse passante per il centro

M   R 2 sin dd  2R 2  sin d  4R 2
0
R
M

4R 2
dI  r 2 dm  r 2dA  r 2 2r  Rd 
M
 r  2R sin d
2
2


M
2
r  R sin 
dI  R sin  
2 R sin  d
2
4R
2 M
M 2
3
dI  R sin  
sin d
dI 
R sin  d
2
2
2
M 2
3
dI 
R sin   d
2

I 

M 2
dI 
R  sin 3  d
2
0


M
M 2
M
2
R  sin d  R 2  cos 2  d cos 

R  1  cos 2  sin d 
2
2
2
0
0
0

3
3
2
3
2





1
1
MR
 cos    MR

    1   1 
 
  cos  0  
 
3
3 2


 3  0  2
2M 2
I
R
3
I
2 2
R 
 R
M 3
2
g