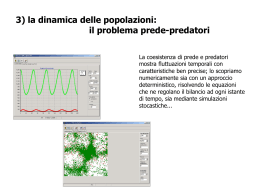
“La realtà… dà i numeri!” Liceo Scientifico “F. Silvestri” a.s.: 2006/2007 Progetto Lauree Scientifiche Convegno conclusivo 8 maggio 2007 “ La Natura è un grande Libro scritto da Dio in lingua Matematica …” Galileo Galilei Un po’ di storia… La nozione di modello risale al secolo VI a.C., quando Pitagora tentò di definire la struttura dell’Universo attraverso l’analisi di numeri che rappresentavano i corpi celesti: era un primitivo tentativo di costruire un modello matematico della realtà fisica. Nel Milleseicento, attraverso il pensiero di Galilei e Newton, sembrò che un insieme di formule e di equazioni potessero spiegare la dinamica di tutti i corpi, e, quindi, dell’Universo intero. Solo nel Milleottocento fu possibile rappresentare molti processi dinamici in termini di equazioni differenziali e integrali, così l’uso di modelli matematici si rivelò un potente mezzo di indagine scientifica, sempre più accurato in relazione all’evolversi delle tecnologie elettroniche ed informatiche. I modelli matematici riguardano diverse discipline, dalla Fisica e la Chimica alla Biologia e l’Ecologia; nella storia recente, la Matematica ha inoltre trovato applicazione anche in settori che coinvolgono decisioni da parte dell’Uomo, quali l’Economia e la Finanza. Distinzioni preliminari DETERMINISTICI: PROCESSI DI TIPO CAUSA - EFFETTO MODELLI STOCASTICI: PROCESSI ALEATORI MODELLI DETERMINISTICI: l’evoluzione del sistema è governata da una legge esprimibile in termini analitici (variabili di input fisse); pertanto, note le equazioni che regolano la dinamica delle variabili ed il loro stato all’istante iniziale, si può determinare il loro stato ad ogni istante futuro. MODELLI STOCASTICI (stocastico = dovuto al caso, aleatorio, dal greco stochastikòs = congetturale) tengono in considerazione le variazioni (causali e non) delle variabili di input, e quindi forniscono risultati in termini di "probabilità". È importante sottolineare che ciò che differenzia i modelli deterministici da quelli stocastici è che in questi ultimi si tiene conto della variabilità dei dati di input. Fasi di studio di un fenomeno RACCOLTA E ANALISI DEI DATI DELLO STATO DEL FENOMENO COSTRUZIONE E STUDIO DEL MODELLO MATEMATICO VALIDAZIONE DEL MODELLO Requisiti di un buon modello SEMPLICITA’ In ogni grafico di quelli proposti il tasso di crescita della variabile dipendente rispetto alla variabile indipendente è costante. Si giunge, dunque, alla determinazione di un modello lineare, il cui grafico è quello di una funzione esponenziale. Questo modello è noto come Modello di Malthus o della “crescita geometrica”. Si tratta, ora, di definire nei dettagli cosa è il tasso di crescita. Sia P una popolazione isolata. Indichiamo con: N(t) il numero di individui che compongono la popolazione all’istante di tempo t; N(t + t) il numero di individui che compongono la popolazione all’istante di tempo (t + t), ossia quando è passato un intervallo di tempo t. Ipotesi di lavoro: N(t) è una funzione continua La variazione di popolazione ΔN = N(t + Δt)-N(t) è proporzionale a N(t) e a Δt secondo una costante di proporzionalità k che viene detta potenziale biologico o tasso di crescita. Il tasso di crescita k è tipico della specie e viene calcolato sperimentalmente. ΔN N(t Δt) N(t) kN (t ) Δt Δt è la misura della variazione della popolazione nell’intervallo di tempo ∆t, ovvero la “velocità media” di variazione della popolazione nell’intervallo di tempo considerato, proporzionale alla popolazione al tempo t. Se si suppone N(t) anche derivabile si può definire Il tasso di crescita istantaneo della popolazione: Dove N N (t ) lim t 0 t N (t ) k N (t ) Vediamo ora se la legge ci dà informazioni sullo sviluppo della popolazione N = N(t) è una funzione di classe C1 del tempo t : N k N = dN 1 = k dt N ln N(t) = kt N(0) N(t) ekt = N(0) t 0 t # N1 dN = #kdt 0 6 @ t lnN 0= kt kt N(t) = N(0) e Naturalmente, per tracciare il grafico occorre conoscere N(0) e il tasso di crescita k, che come abbiamo osservato sono dati sperimentali. Il modello di Malthus può rappresentare la crescita biologica solo in un intervallo di tempo limitato. Infatti, nel caso k>0 si osserva, lim N (t ) t conseguenza inaccettabile perché prevede la crescita esponenziale della popolazione che dovrebbe essere accompagnata da una crescita illimitata di cibo a disposizione. Perfezioniamo… Il modello di Verhulst elimina il paradosso del modello di Malthus, assumendo che il tasso di crescita decresca al crescere della popolazione e sottraendo alla costante K che rappresenta il tasso di crescita malthusiano una quantità hN(t) che cresce al crescere della popolazione. K k hN (t ) k 0, h 0 Ora, quanto più numerosa sarà la popolazione, tanto più piccolo sarà il tasso di crescita. Il prodotto hN(t) rappresenta l’esistenza di vincoli esterni (influenza dell’ambiente, interazione degli individui, …) che frenano la crescita della popolazione. Otteniamo quindi: : N (t) k hN(t) = N(t) In essa, al crescere di N(t), il termine hN(t) diventa sempre più grande fino a che il tasso di crescita k – hN(t) diventerà zero: k - hN(t) = 0 & N(t) = k h Quindi, la crescita della popolazione non è più illimitata, ma non può superare il valore limite dato da k/h, che rappresenta la capacità di accoglienza dell’ambiente e, come le altre costanti, è determinata sperimentalmente. Il modello di crescita logistica è descritto dall’equazione: : 6 @ N (t) = k - hN(t) N(t) dal grafico, la cosiddetta “curva a S”, si rileva che N(t) cresce a partire dal valore N(0) sempre più rapidamente, poi rallenta la crescita e tende infine verso il valore della popolazione limite k/h che non può superare. La matematica delle popolazioni a servizio del marketing I modelli di diffusione di prodotti e servizi Alcuni problemi legati alla gestione del successo (ciclo di vita di un prodotto): Quale può essere la massima diffusione di un prodotto o di un servizio? A che punto intervenire con campagne pubblicitarie a supporto dell’offerta? Come provvedere ad un suo eventuale “restyling”? Come reagire all’ingresso di un eventuale concorrente nella nicchia di mercato? Ipotesi per l’utilizzo del Modello di Malthus mancanza di concorrenti, e quindi di possibili scelte da parte del cliente; bacino di utenza isolato, ossia la propensione all’acquisto è indipendente da stimoli esterni, come ad esempio l’andamento economico e la pubblicità; comportamento omogeneo del cliente, in cui sono trascurabili differenze strutturali quali età, sesso, distribuzione geografica; comportamento del cliente invariante nel tempo:il tasso di acquisto e di abbandono di un prodotto può ritenersi costante. Il modello di Malthus, quindi, lega la variabile tasso di acquisto (il numero medio di prodotti acquisiti per cliente) con il tasso di abbandono (numero medio di prodotti abbandonati per cliente). Il risultato è una crescita esponenziale della vendita del prodotto: N(t) t Problema: il numero dei potenziali clienti è sempre finito. Soluzione: modello logistico Indipendentemente dalla condizione iniziale di mercato, a regime, la penetrazione del prodotto si stabilizzerà sul valore K. Ciò ha delle conseguenze, in ambito marketing, immediate: il massimo dello sforzo pubblicitario deve essere fatto in fase di lancio e al termine dell’andamento lineare, in modo da allontanare il più possibile l’istante in cui il tasso di penetrazione si avvicini a K; la differenziazione dell’offerta può avvenire durante la fase di crescita “lineare” della diffusione del prodotto; quando il gap tra K e la funzione logistica è minore di un valore stabilito a priori dal marketing, il ciclo di vita del prodotto si può considerare concluso. Problema: il numero dei potenziali clienti è sempre finito. Soluzione: modello logistico PREDAZIONE: MODELLO DI LOTKA-VOLTERRA L’origine del modello preda-predatore di Lotka-Volterra fu ispirato dagli studi di alcuni zoologi italiani che, dopo la prima guerra mondiale, avevano rilevato che nell’alto Adriatico, quando le attività di pesca erano diminuite, era aumentato il numero di alcuni pesci predatori mentre era diminuito quello dei pesci preda. NELLA INTERAZIONE TRA SPECIE I COSTITUENTI UNA POPOLAZIONE N2 - PREDATORI - SI NUTRONO MANGIANDO I COSTITUENTI DI UNA POPOLAZIONE N1 - PREDE GLI ASSIOMI DEL MODELLO DI LOTKA-VOLTERRA SONO: 1) in assenza di predatori, le prede che dispongono di cibo in quantità illimitata (plancton) crescono con legge malthusiana: : N1= aN1 2) in presenza di predatori, il tasso di crescita delle prede diminuisce di una quantità proporzionale al numero dei predatori: : N1 a bN2 N1 = - : & N1= aN1- bN1N2 3) in assenza di prede, quindi senza cibo, i predatori si estinguono con legge malthusiana: : N2= - cN2 4) in presenza di prede, il tasso di crescita dei predatori aumenta di una quantità proporzionale al numero delle prede; : N2 c + dN1 N2 = - : & N2= - cN2+ dN1N2 Dagli assiomi, si ottiene il seguente sistema di equazioni differenziali che rappresenta IL MODELLO DI LOTKA - VOLTERRA: : * N= 1 aN1- bN1N2 : N2= - cN2+ dN1N2 Dall’analisi qualitativa del sistema si ottiene che: il numero di individui delle due popolazioni oscilla “periodicamente”. L’ANALISI QUALITATIVA DELLE TRAIETTORIE DEFINITE DAL MODELLO DI LOTKA-VOLTERRA CONSENTE DI AFFERMARE CHE L’INCREMENTO NATURALE DELLE PREDE PORTA A UN’ACCRESCIUTA ATTIVITÀ DI PREDAZIONE, DI CONSEGUENZA IL NUMERO DEI PREDATORI CRESCE MENTRE QUELLO DELLE PREDE DECRESCE. CIÒ ACCADE FINO A QUANDO IL NUMERO DELLE PREDE DIVENTA TROPPO PICCOLO PER LE ESIGENZE DEI PREDATORI CHE PERTANTO COMINCIANO A ESTINGUERSI. QUANDO LA POPOLAZIONE PREDATRICE DECRESCE, DIMINUISCE LA PRESSIONE SULLE PREDE CHE COSÌ RICOMINCIANO A CRESCERE DI NUMERO E IL CICLO RIPRENDE. INTRODUCENDO NEI DATI DEL PROBLEMA LA PERTURBAZIONE RAPPRESENTATA DALLA PESCA (PRELIEVO INDISCRIMINATO E UNIFORME DELL’UNA E DELL’ALTRA SPECIE), IL MODELLO DIVENTA: : * N= 1 aN1- bN1N2- f N1 : N2= - cN2+ dN1N2- f N2 DOVE ε ESPRIME L’UNIFORME INTENSITA’ DELLA PESCA. QUESTA VARIAZIONE FRENA LA CRESCITA DI ENTRAMBE LE POPOLAZIONI PROPORZIONALMENTE AL LORO NUMERO. Ciò significa che l’essenza stessa delle “leggi” della natura e, più in generale, della realtà è racchiusa in un’equazione matematica? Alunni partecipanti: Ascione Cristina Avallone Claudio Barbaro Eliana HannoMaria presentato: Brunetti Brigida De Matteo Ilaria Buccini Daniela Maria Rossano Lucia Liceo Scientifico Celentano Manuela Stuvard Salvatore CoppolaSilvestri” Valentina “Filippo Presentazione realizzata De Gaetano Davide da: Portici De Matteo Ilaria Cino Fabrizia Di Natale Concetta Esposito Darjn Papillo Lorenzo Riccardi Carla Rossano Lucia Stuvard Salvatore Zappia Sonia
Scaricare