Sistemi dinamici discreti non lineari
xk 1  f ( xk )
f non lineare
Definizione : dato un s.d.d { I , f }, un numero   R si dice equilibrio ( o
punto fisso o punto stazionario )
se vale :  = f()   I
Esempi
L’algoritmo di Newton
l’approssimazione delle soluzioni di una
equazione
g(x)=0,
g(x) derivabile
g(x)
Eq. tangente
y  g ' ( x0 )( x  x0 )  g ( x0 )
0  g ' ( x0 )( x  x0 )  g ( x0 )
x  x0  
x
g ( x0 )
g ' ( x0 )
g ( x0 )
 x0
g ' ( x0 )
xt 1  xt 
g ( xt )
g ' ( xt )
Eq. Alle differenze finite lineare o non lineare?
.
Problema: approssimare
N
x N 0
2
Applichiamo Newton a:
x  N x  N 1
N
x x 

  x  
2x
2x
2
x 
t 1
2
2
t
t
t
t
t
t
L’incognita è Il punto fisso è x*=
Problema: approssimare
3
(1)
t
N
N
x N 0
3
Applichiamo Newton a:
x  N 2x  N
x x 

3x
3x
t 1
t
3
3
t
t
2
2
t
t
algoritmi di questo tipo sono implementati nelle calcolatrici scientifiche.
Abbiamo ottenuto equazioni alle differenze finite non lineari che determinano
una successione di valori (convergenti ?)
Affinché l’equilibrio di Newton dia origine ad una successione
convergente (sia stabile), vale un condizione di stabilità simile a
quella delle equazioni lineari
Con x t+1=f(x t) invece di xt+1=a xt+c
xt 1  xt 
g ( xt )
g ' ( xt )
g ( x)  x 
g(x )
f ' ( x*)  1
g'(x )
La convergenza dipende quindi anche da x*. Se, come nel caso del problema (1), x* non
lo conosciamo ma lo vogliamo approssimare, calcoliamo la condizione di convergenza dal
punto iniziale x0, che si spera essere sufficientemente vicino a x* in modo che le proprietà
(derivata) della g non cambino.
Si può verificare facilmente che per qualunque x0<0 la successione (1) converge a  2
mentre per x0>0 converge a 2
Nei sistemi lineari questo non avviene.
Problema: approssimare gli zeri (
1
 1
  0  1
2
3
) di
x x0
3
Applichiamo Netwon
x x
2x
x x 

3x  1 3x  1
3
3
t
t 1
t
t
t
2
2
t
t
Ha 3 punti fissi
In generale le equazioni alle differenze finite non lineari hanno
più punti fissi e per ognuno si deve studiare la stabilità
(calcolare le derivate)
A differenza del caso lineare, non si sanno esplicitare le
soluzioni analitiche salvo casi particolari.
Rappresentazione delle soluzioni
xk+1
xt
x0
xk
t
Definizione : l’insieme di tutte le traiettorie al variare di x0 si
chiama quadro degli stati (o delle traiettorie)
Xk+1
Per vedere geometricamente il punto fisso
Nello spazio degli stati
CONDIZIONI DI STABILITA’
Teorema : (condizione del primo ordine di stabilità)
Se  è un equilibrio per il s.d.d. { I , f } e f è di classe C 1 allora :
f ( )  1  
f ( )  1  
è localmente asintotica mente stabile
è instabile
Teorema : (condizione del secondo ordine di stabilità)
Se  è un equilibrio per il s.d.d. { I , f } con f di classe C 2 e
f () = 1 allora :
f ( )  0  
f ( )  0  
inferiorme nte asintotica mente stabile

superiorme nte repulsivo
superiorme nte asintotica mente stabile

inferiorme nte repulsivo
Esempio 1
xn 1  xn 4  xn3  xn  y( xn )
y(0)  1
y(0)  0
y(0)  6  0
 repulsivo
Esempio 2
xn 1  xn 4  xn3  xn  y( xn )
y(0)  1

y(0)  0
attrattivo
y(0)  6  0
Teorema : (condizione del terzo ordine di stabilità)
Se  è un equilibrio per il s.d.d. { I , f } con f è di classe C 3 ,
f () = 1, f () = 0 allora :
f ( )  0  
f ( )  0  
è repulsivo
è localmente asintotica mente stabile
Teorema : Sia f : I  I con f  C 3, f () = , f () = -1 allora :
2 f ( )  3( f ( )) 2  0  
2 f ( )  3( f ( )) 2  0  
è localmente asintot. stabile
è instabile
Schema riassuntivo per lo studio della stabilità di un equilibrio 
quando f è dotata di derivate.
l.a.s =
s.l.a.s =
i.l.a.s =
r. =
s.r. =
i.r. =
localmente asintoticamente stabile
superiormente localmente asintoticamente stabile
inferiormente localmente asintoticamente stabile
repulsivo
superiormente repulsivo
inferiormente repulsivo
ORBITE PERIODICHE (CICLI)
Definizione : Sia { I , f } un s.d.d.
un ciclo di ordine s (o orbita periodica di (minimo) periodo s, o
s-ciclo) è un insieme di s valori in I {0 , 1 , s-1 } diversi tra loro
e tali che :
1 = f (0)
2 = f (1)
……
0 = f (s-1)
s = periodo dell’orbita ( o ordine del ciclo )
Le orbite di periodo s si trovano calcolando i
punti fissi di f s(x) = x
xt
Xt+1
1
0
2
f
1
s=3
0
2
t
xt
Esempio :
il s.d.d. { (0,+), f (x) = 1/x } presenta un solo punto di equilibrio  = 1
ed  orbite periodiche { x0 , x0 - 1 }
xk 1 
xk+1
1
 f ( xk )
xk
x0
1 / x0
1 / x0
x0
xk
Equilibrio ed orbite periodiche di { (0,+), 1/x }
STABILITA’ DELLE ORBITE PERIODICHE
localmente attrattivo
repulsivo
Esempio

E’ un teorema molto semplice da applicare se è noto l’ s-ciclo.
La vera difficoltà consiste nel sapere se esiste un s-ciclo e nella sua
determinazione.
Esempio :
2
se f ( x)  4( x  x ) e I  [0,1]
per determinare un 4-ciclo si devono trovare i punti fissi di
f 4 ( x)  f ( f ( f ( f ( x))))
cioè
f 4 ( x)  x
che è un’equazione di 16° grado !!
esempio

f 2 ( x)  f ( f ( x))  4 4( x  x 2 )  [(4( x  x 2 )]2

MAPPA LOGISTICA
Evoluzione di una popolazione
MALTHUS
y k 1  y k  ay k  (1  a ) y k
r =1+a> 1
 la popolazione cresce
0<r<1  la popolazione decresce
è un modello di crescita esponenziale 
crescita illimitata (inadatto nel lungo periodo)
Correzione di VERHULST
Risorse limitate: la velocità di crescita diminuisce proporzionalmente alla popolazione
yk 1  (r  yk ) yk  ry k  yk
2
r,>0
se H = r / 
xk = yk /H 
y 

yk 1  ryk 1  k 
H

xk 1  rxk 1  xk 
xk 1  xk 1  xk 
r,H>0
r>0
DINAMICA DELLA CRESCITA LOGISTICA
xk 1  xk 1  xk 
0 4
affinchè
mappa logistica
max f ( x)  1
0 x1
xk 1
xk 1
1
/4
0
1/ 2
1
xk
0
1
 =1/2, 1, 2, 3, 4
xk
PUNTI DI EQUILIBRIO DELLA LOGISTICA AL VARIARE DI 
xt 1  f ( xt ,  )  xt 1  xk 
 0
punti di equilibrio
punti di equilibrio

x  λx 1  x
*
*
*

x1*  0
*2
 λx
 1  λ x*  0
x2* 
vediamo se sono asintoticamente stabili :

*
* 
f ( x )    2x  
2


( x*  0)
( x* 
 1
)

 1

x*  0
x* 
 1

è asintotica mente stabile  0    1
è asintotica mente stabile   1  2    1

 3    1
 1   3
si può osservare che :
per 0    1 l' unico punto di equilibrio è x*  0
(perché la funzione interseca la
xt+1
bisettrice una volta sola)
xt
per 1    3 gli equilibri sono due :
x*  0
instabile
e
x* 
 1

asintoticamente stabile
xt+1
xt
per   1 vi è un cambio di stabilità di x*  0
che si può rappresentare geometricamente così:
x*
asintoticamente stabile
instabile
1

per 1    3 vi sono 2 punti di equilibrio : uno stabile ed uno
instabile:
x*
x*  (  1) / 

1
3
Cosa succede per   3 ?
La soluzione x*  (  1) /  diventa instabile e compare una
soluzione di periodo 2 :
xt+1
x*
x* 
(  1)
=3.4


1
3
3.449
Si dimostra che ciò avviene fino a quando
  3 è
3    3.449 un punto di biforcazione
(a forchetta o di raddoppiamento del periodo)
xt
  3.449 la soluzione di periodo 2 diventa instabile e compare
una soluzione di periodo 4
x
xk+1
*
xk

1 3 3.449
3.55
i valori visitati si trovano
cercando i punti di f 4(x)
  3.55 avviene la transizione al periodo 8
I valori di  in cui avvengono i cambi di stabilità si avvicinano tra
di loro e tendono a   3.57
Dopo tale valore il sistema mostra un comportamento caotico
Benchè generato da un sistema deterministico ha le caratteristiche
di un sistema random
COSTANTE DI FEIGENBAUM
F = 4.6692016091029
k  k 1
F
k   k 1  k
lim
il numero è una costante universale (come  , e )
osservazioni
• La presenza di non linearità può portare al
caos
• Con il caos compare la sensibilità alle
condizioni iniziali
• In presenza di caos la predizione, anche per
un sistema deterministico con poche
equazioni, diventa praticamente impossibile
Alcune caratteristiche di un sistema caotico:
Sensibilità alle condizioni iniziali
Mappa logistica,=3.9,
30 iterazioni.
Il comportamento della soluzione è molto vario
Teoria delle biforcazioni
Alcuni tipi di diagrammi di biforcazione
Diagramma di biforcazione di f ( x,  ) :
punti fissi
di f
parametro
biforcazione transcritica
biforcazione a forchetta (Hopf)
x
x

punti fissi asintoticamente stabili
punti fissi instabili

biforcazione tangente
(nodo-sella)
biforcazione con raddoppio
(flip)
x
linea di
punti fissi

f ( x,  )    x  x2
x
punti periodici
di periodo 2
x  x ( )

f ( x,  )  (1   ) x  (k   ) x2
k 0
LOGISTICA
SISTEMI NON LINEARI
 xt  f ( xt 1, yt 1)

 yt  g ( xt 1, yt 1)

 x*  f ( x* , y * )
( x , y ) è un punto d' equilibrio   *
* *

 y  g(x , y )
*
*
* *
studiamo la stabilità del sistema nelle vicinanze di ( x , y )
Supponiamo f e g continue e derivabili
* *
 espandiamo il sistema in ( x , y ) usando una serie di Taylor:

f ( x* , y* )
f ( x* , y* )
*
*
( xt 1  x ) 
( yt 1  y* )
 xt  x 
xt 1
yt 1


* *
* *
 y  y*  g ( x , y ) ( x  x* )  g ( x , y ) ( y  y* )
t
t 1
t 1


x

y
t

1
t

1

ponendo :
f ( x* , y* )
a11 
xt 1
g ( x* , y* )
a21 
xt 1
f ( x* , y* )
a12 
yt 1
g ( x* , y* )
a22 
yt 1
 xt  x*   a11 a12   xt 1  x* 



*  a
*
 yt  y   21 a22   yt 1  y 
J = matrice jacobiana
(nel caso di un sistema lineare è la matrice dei
coefficienti)
t  At 1
PUNTI FISSI IPERBOLICI
Definizione :
Supponiamo che 1 2 siano gli autovalori dello jacobiano.
* *
Il punto fisso ( x , y ) si dice :
iperbolico se 1  1 e 2  1
(se sono complessi si considera la parte reale)
non iperbolico se 1  1 o 2  1
TEOREMA DI HARTMAN GROSSMAN
Nelle vicinanze di un punto fisso iperbolico il sistema non lineare
si comporta come quello lineare ovvero ha la stessa stabilità.
Se tutti gli autovalori nell’intorno di un punto di equilibrio sono,
in modulo, <1 allora l’equilibrio è stabile e localmente attrattivo.
SISTEMA DI HENON
MICHAEL HENON
Nato a Parigi nel 1931 , astronomo dell’osservatorio di Nizza.
Voleva modellizzare le orbite delle stelle intorno ai centri delle loro galassie.
Henon considerò i centri gravitazionali come oggetti 3-d (invece che oggetti
puntiformi ovvero 0-d )
Per semplificare lo studio delle orbite delle stelle considerò la loro intersezione
con un piano.
Dopo circa 12 intersezioni i punti incominciarono a disegnare una forma che
sembrava la sezione di un toro.
Henon cercò di fare previsioni circa le intersezioni future dell’orbita con il
piano.
Infine, usando le differenze finite, trovò il seguente modello :
a

 xt 1  yt  1.4  xt2  1


 yt 1  0.3  xt
b
dinamica
caotica
Calcoliamo i punti fissi di Henon
 xn 1  1  a  xn2  y n

 y n 1  b  xn
punti fissi
xn 1  xn  x *
yn 1  xn  y *
 x*  1  ax *2  y *
 x*  1  ax *2 bx *

 y*  bx *
(b  1)  (1  b) 2  4a
x *1, 2 
,
2a
 ax *2  x * (1  b)  1  0
 (b  1)  (1  b) 2  4a 

y *1, 2  b


2a


2
(
1

b
)
 4a  0
 La mappa di Henon ha 2 punti fissi 
esempio :
a  3 / 16 b  1/ 2  i punti fissi sono A  (-4,-2) B  (4 / 3,2 / 3)
lo Jabobiano :
  2ax 1 

J  
0
 b
Gli autovalori di J in A sono 1  0.28 2  1.78
 A è un punto di sella
Gli autovalori di J in B sono 1  1 e 2  0.5

il punto B è non iperbolico
Per altri valori di a e b:
b  0.4 a  0.2
b  0.4 a  0.5
b  0.4 a  0.9
orbita periodo 1
orbita periodo 2
orbita periodo 4
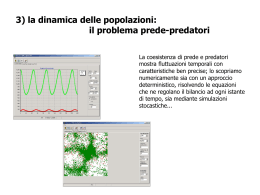
Modello di Lotka-Volterra
Il modello di Lotka-Volterra è il più semplice tra i modelli di
preda predatore. Il modello è stato sviluppato
indipendentemente da Lotka (1925) e da Volterra (1926).
A metà degli anni 20 il biologo Umberto d’Ancona studiava le
variazioni delle popolazioni di varie specie di pesci che
interagivano l’una con l’altra: squali, etc. e pesci
commestibili. D’Ancona si rivolse ad un famoso matematico
italiano: Vito Volterra
Vito Volterra suddivise tutti i pesci in due popolazioni, quella delle prede x(t) e quella
dei predatori y(t), e fece le seguenti ipotesi:
Le prede non competevano molto intensamente fra loro nella ricerca di cibo, quindi, in
assenza di predatori, il numero di prede (commestibili) cresceva in accordo con la
legge di Malthus x(t+1)=x(t)+ax(t)
per qualche costante positiva a.
La presenza di predatori faceva si che il fattore di crescita non fosse costante ma
decrescesse linearmente con il numero di predatori:
x(t+1)=x(t)+(a-b.*y(t)).*x(t);
Analogamente i predatori in assenza di prede avevano un naturale tasso di decrescita –
dy(t) dovuto ai decessi e proporzionale al loro numero attuale. La presenza di prede
faceva si che il loro numero aumentasse proporzionalmente al numero delle prede x.
Perciò
y(t+1)=y(t)+(c.*x(t)-d).*y(t);
a,b,c,d erano costanti >0. Si può verificare che l’unico equilibrio non banale è: (d/c, a/b)
ma si tratta in generale di un equilibrio instabile.
a=0.1; d=0.2; b=0.1; c=0.1;
Analizziamo graficamente lo spazio delle fasi
del sistema
A = troppi predatori: inizia a diminuire il numero di prede.
B = poche prede i predatori diminuiscono.
C = I predatori sono così pochi che le prede possono aumentare.
D= molte prede, pochi predatori: I predatori possono aumentare.
Goodwin’s model
Richard Goodwin (1967) formulò un modello non-lineare dei cicli economici
basato sulla lotta di classe: datori di lavoro-lavoratori, tramite le equazioni di
Lotka-Volterra .
Il modello di Goodwin cerca di dimostrare la relazione ciclica tra il lavoro e il
salario in una economia basata sul lavoro.
Le caratteristiche principali del modello sono le seguenti: alta occupazione
genera inflazione nei salari che li può far aumentare; ciò, a sua volta, riduce i
profitti dei capitalisti e così riduce gli investimenti futuri e la produzione. Tale
riduzione della produzione riduce a sua volta la domanda di lavoro e l’ inflazione
dei salari. I salari dei lavoratori diminuiscono. Ma non appena i salari
diminuiscono i profitti aumenteranno e con essi gli investimenti. Ciò porta di
nuovo all’aumento dell’occupazione e poi dei salari. Il ciclo quindi si ripete.
Bibliografia
http://www.cmp.caltech.edu/~mcc/Chaos_Course/Outline.html
http://www.enm.bris.ac.uk/staff/berndk/chaosweb/