POPOLAZIONI INTERAGENTI
In natura nessuna popolazione è isolata.
Nel caso di due specie che condividono un ecosistema si può avere:
Competizione -Mutualismo
Predazione-parassitismo
p (t )
Popolazione delle prede
q (t )
Popolazione dei predatori
In assenza di predatori:
• le prede aumentano
• in modo proporzionale (ipotesi del modello)
dp
 A * p (t )
dt
A0
tasso di accrescimento
In assenza di prede:
• I predatori diminuiscono (muoiono di fame)
• in modo proporzionale
dq
  D * q(t )
dt
D0
Tasso di mortalità
Introduciamo l’interazione tra le specie
MODELLO
DI
LOTKA-VOLTERRA
Alfred James Lotka
demografo americano
(1880-1949)
Vito Volterra
matematico italiano
(1860-1940)
dp
 A * p (t )  f ( p, q )
dt
interazione
dq
  D * q (t )  g ( p, q )
dt
La forma del termine di interazione segue la nota legge
di massa azione della chimica:
La velocità di collisioni molecolari di due specie chimiche
in una soluzione è proporzionale al prodotto delle due
concentrazioni
f ( p, q )
Interazione delle prede con i predatori:
proporzionale a p (tasso di mortalità)
proporzionale a q (incontri)
f ( p, q )   * p * q

coefficiente di predazione per le prede
Interazione dei predatori con le prede:
g ( p, q )
proporzionale al numero di prede (incontri-cibo)
proporzionale al numero di predatori
g ( p, q )   * p * q



coefficiente di
predazione dei predatori
efficienza di predazione
Equazioni
di
Lotka-Volterra
dp
 Ap  pq
dt
dq
  Dq   pq
dt
Sistema differenziale
del I ordine
Quesiti
• Cosa cambia rispetto i modelli precedenti ad 1 popolazione
• Come si comportano le due popolazioni a ”lungo andare”
• Le popolazioni raggiungono un equilibrio?
• E’ reale il rischio di estinzione delle prede?
STABILITA’
DI SISTEMI DIFFERENZIALI
DEL I ORDINE
dx
 f1 ( x , y )
dt
dy
 f 2 ( x, y )
dt
t fissato:
la coppia (x(t), y(t) ) può essere vista come un punto di coordinate (x,y)
oppure come il vettore posizione x(t)=[ x(t), y(t)]
( x(t ), y (t ))
( x0 , y0 )
 x0 , y0 
x(t)=[ x(t), y(t)]
Al variare di t
il punto (x(t), y(t) ) descrive una traettoria che rappresenta graficamente la
soluzione del sistema di equazioni
Vettore velocità

Il vettore
dx  dx dy 
 , 
dt  dt dt 
rappresenta la variazione istantanea in x e in y
è chiamato vettore velocità

dx  dx dy 

,
dt  dt dt 
tangente alla curva soluzione
Piano delle fasi

E’ l’insieme delle direzioni:
dx  dx dy 
 , 
dt  dt dt 
Esempio di spazio delle fasi
Nel piano delle fasi è
importante
stabilire la posizione
dei punti (x, y) in cui
il vettore  dx , dy 
è nullo.  dt dt 
In tali punti le
variazioni delle
funzioni x(t) e y(t)
risultano nulle
Sono pertanto i punti stazionari o punti di equilibrio

Nei punti in cui il vettore
dx
0
dt
dx  dx dy 
 , 0
dt  dt dt 
risulta:
dy
0
dt
I punti stazionari sono l’intersezione dell’insieme di
dx
 0 (x nullcline) con l’insieme di punti in
punti in cui
dt
dy
 0 (y nullcline)
cui
dt
dx
 0 il vettore direzionale è parallelo all’asse y
Nei punti in cui
dt

dx  dx dy 

,
dt  dt dt 

dy
dt
dx  dy 
 0, 
dt  dt 
dx
dt
x nullcline
Nei punti in cui dy  0 il vettore direzionale è parallelo all’asse x
dt

dx  dx 
  ,0 
dt  dt 
y nullcline
Stati di equilibrio e diagramma delle fasi
del modello Lotka-Volterra
dx
 x ( A  y )
dt
dy
  y ( D  x)
dt
Equilibrio: le popolazioni non cambiano
derivate nulle
x0
y0
x ( A  y )  0
y ( D  x)  0
x 
*
D

y 
*
A

dy
0
dt
P2
y  A/
P1
dx
0
dt
x  D/
Per il significato biologico ha interesse solo il quadrante x  0, y  0
Le rette
x
D

e
y
A

sono le due nullcline
dy
0
dt
IV
I
P2
y  A/
dx
0
dt
II
III
P1
x  D/
f1
dx
 x ( A  y )
dt
dy
  y ( D  x) f 2
dt
zona
f1
f2
I
<0
<0
II
>0
<0
III
>0
>0
IV
<0
>0
dy
0
dt
IV
I
P2
y  A/
II
P1
dx
0
dt
III
x  D/
In assenza di prede (x=0) il punto P1 è attrattivo: estinzione
(I predatori sopravvivono solo se ci sono le prede)
P1 invece è repulsivo per le prede in assenza di predatori (y=0)
(le prede aumentano se non ci sono i predatori)
Il Punto P2:
(D /  , A /  )
OSSERVAZIONI
• Il livello di equilibrio della popolazione x (prede) è D /  e quindi non
dipende dai parametri della popolazione x , ma dipende dai parametri
associati ai predatori.
D   *x )
Affinchè le prede siano stazionarie, ( x  D / 
debbono crescere in modo che il tasso di predazione dei predatori (  * x )
si mantenga uguale al tasso di mortalità dei predatori D
A /  e quindi non
dipende dai parametri della popolazione y, ma dipende dai parametri associati
alle prede
• Il livello di equilibrio della popolazione y (predatori) è
A  y )
Affinchè i predatori si mantengano stazionari, ( y  A / 
il tasso di mortalità dovuto alla predazione  * y
deve mantenersi
uguale al tasso di accrescimento A delle prede
dy
0
dt
IV
I
P2
y  A/
II
P1
dx
0
dt
III
x  D/
Attorno a P2 le traettorie hanno un comportamento ciclico:
ad un aumento delle prede segue un aumento dei predatori, che a sua volta
provoca una diminuizione delle prede, seguita da una diminuizione dei predatori e
così via …
Esiste un equilibrio “precario”
tra le forze che portano ad oscillazioni che aumentano
e le forze che portano ad oscillazioni che diminuiscono
Piccoli cambiamenti nel sistema possono rompere tale equilibrio
Centro neutrale strutturalmente instabile
Caso generale
Si possono avere diverse situazioni
(t   )
Le traettorie potrebbero convergere a P2 seguendo delle spirali
Spirale stabile
Oppure le traettorie potrebbero descrivere delle curve
di forma ellittica attorno al punto P2
Centro neutrale
Oppure le traettorie potrebbero allontanarsi da P2,
seguendo delle spirali
Spirale instabile
Il modello di Lotka –Volterra
non è ecologicamente stabile
Si può dimostrare che il punto P2 del modello di Lotka-Volterra
è un centro neutrale
Le soluzioni x e y girano attorno al punto P2.
Il punto stazionario non è attrattivo, cioè non è
asintoticamente stabile
Inoltre:
se la soluzione è perturbata a partire da una determinata orbita, essa
non torna all’orbita iniziale, ma piuttosto segue una nuova orbita.
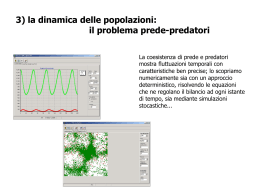
Dinamica e piano delle fasi
di due popolazioni di tonni e squali
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
Problema preda-predatore
%
Modello di Lotka-Volterra
%
%
X'(t) = A X(t) - alpha X(t)Y(t)
%
Y'(t) = - D Y(t) + Beta X(t)Y(t)
%
X(0) = x0
Y(0) = y0
%
% A
tasso di crescita della preda
% alpha
coefficiente di predazione della preda
% D
tasso di mortalità dei predatori
% Beta
coefficiente di predazione del predatore
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all
global A alpha D Beta
A =1;alpha=0.1;D=1;Beta=0.2;
%Alpha=1;Beta=0.2;Gamma=1;Delta=0.1;
t0=0;
tf=20;
tspan=[t0,tf];
y0=[6 2]';
h= 0.01;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
Risoluzione del sistema
%
di equazioni differenziali
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
options = odeset('OutputFcn',@odephas2);
[t,y] = ode23s(@fvolt, tspan, y0,options);
figure(2)
subplot(2,1,1),plot(t,y)
title('Soluzioni del problema di Lotka-Volterra')
xlabel('tempo'); ylabel('popolazioni')
legend('preda','predatore')
subplot(2,1,2),
plot(y(:,1),y(:,2),'b',D/Beta,A/alpha,'o')
function F=fvolt(t,z)
global A alpha D Beta
F=[A*z(1) - alpha*z(2)*z(1); -D*z(2) + Beta*z(1)*z(2)];
return