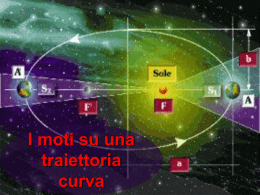
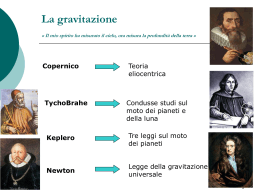
Meccanica
2013-2014
Gravitazione
19
Gravitazione
Forza
Mediatore
Intensità
relativa
Andamento
asintotico
Raggio
d'azione
Interazione forte
gluone
1038
r0
10-15 m
fotone
1036
1/r2
bosoni Z,
W+ e W-
1025
(1/r) exp(-r/r0)
gravitone?
100
1/r2
Interazione
elettromagnetica
Interazione
debole
Gravità
Campo di forze centrali
10-18 m
Centro della forza
- La forza in qualsiasi punto P è nella direzione OP
r
=
r
- Il modulo della forza in P è funzione solo di
OP
F = ± F (r )ur
(attrattiva, repulsiva)
F (r )
r = ru r
P
O
• Teorema
del momento angolare per una forza centrale
dL = r × F = r × F (r )ur = 0
dt
• Piano della traiettoria:
L = r × mv
L ⊥ (r , v )
Costante
In un campo di forze centrali
il vettore momento angolare
si conserva
Posizione e velocità
(quindi traiettoria)
si mantengono sempre
sullo stesso piano
L
O
r
v
Forze centrali
L
O
r
• Velocità areale:
vθ
v
vr
L = r × mv = r × m(vr + vθ ) = r × mvθ
1 2
dA
2 dθ
dA
r dθ
=
L = rmvθ = mr
= 2m
2
O
dt
dt
= ωr
r
dA L
La “velocità areale” dA/dt
r dθ
=
= Cost.
rimane
costante
dt 2m
2
Orbita
2m
π
r
2π r 2π
A L
2mA
circolare:
=
T
=
=
Orbita chiusa:
=
T=
v
ω
mvr
T 2m
L
F
• Lavoro di una forza centrale
F = ± F (r )ur
B
B
W = ∫ F (r )u r ⋅ ds = ∫ F (r )dr
A
dr θ ds
P
A
r
= f (rB ) − f (rA )
Le forze centrali sono conservative
B
ur
A
rA
O
rB
u r ⋅ ds = ds cos θ = dr
Gravitazione
Forze centrali
F (r )
Definizione:
r = ru r
F = ± F (r )ur
P
O
Proprietà:
1. Il momento angolare si
conserva
2. La traiettoria si
mantiene sullo stesso
piano
3. La “velocità areale” è
costante
4. Le forze centrali
sono conservative
dL
=0
dt
L ⊥ (r , v )
L
O
r
v
Costante
dA
L
=
= Const
dt 2m
B
dA =
O
r
r dθ
W = ∫ F (r )u r ⋅ ds = f (rB ) − f (rA )
A
1 2
r dθ
2
Gravitazione
Da Keplero a Newton
Le tre leggi di Keplero
Descrizione empirica del moto dei pianeti
Basate sulle osservazioni di Tycho Brahe (1546-1601)
I - Le orbite dei pianeti sono ellittiche,
il Sole occupa uno dei fuochi
(La più rivoluzionaria!)
∆t
P
a
S
∆t
II - La velocità areale del raggio
che unisce il sole al pianeta è
costante: ∆A
b
∆t
= Const
La velocità del pianeta non è costante
Giovanni Keplero
(1571 – 1630)
III - Il quadrato del periodo di rivoluzione è proporzionale
al cubo del semiasse maggiore
T 2 = kS a3
Eccentricità:
La stessa costante per le orbite di
tutti i pianeti intorno al Sole
b2
ε = 1− 2 ≤ 1
a
ε =0
cerchio
Area:
A = πab = πa 2 1 − ε 2
Orbita
ellittica
Orbita circolare con lo
stesso raggio medio
Da Keplero a Newton
Moto della Terra intorno al Sole Forza (“di gravità”)
Assume orbita circolare. II Legge di Keplero:
dA
1 dθ
= Cost. = r 2
dt
2 dt
dθ
= Cost.
dt Moto circolare uniforme
Forza centripeta
2
2
4
π
4
π
m
F = mω 2 r = m 2 r =
T
kS r 2
III Keplero:
T 2 = kS r 3
La forza è inversamente
proporzionale al quadrato
della distanza
Newton ipotizza che questa legge valga per due masse qualsiasi
Forza che il Sole esercita sulla Terra:
FS ,T
4π 2 mT
=
kS r 2
Dev’esserci una analoga forza che la Terra esercita sul Sole:
Principio di azione-reazione:
FS ,T = FT , S
4π 2 mT 4π 2 mS
=
2
kS r
kT r 2
4π 2
4π 2
=
≡ G(TS )
Definiamo:
mS k S mT kT
FS ,T
FT , S
Isaac Newton
(1642 – 1727)
4π 2 mS
=
kT r 2
4π 2 1
4π 2 1
=
2
k S mS r
kT mT r 2
mS mT
= G(TS ) 2 = FT ,S
r
Gravitazione universale
FS ,T = FT ,S
mS mT
= G(TS ) 2
r
Vale solo per Sole-pianeti?
Legge universale?
G(TS ) = G per qualunque m1 e m2
Verifica: Forza peso
Corpo di massa m nei pressi della superficie terrestre:
F =G
mT m
rT2
Corpo a simmetria sferica (Terra)
Come se tutta la massa fosse
concentrata nel centro
Se eguaglia la forza peso:
mT m
G 2 = mg
rT
GmT
g= 2
rT
rT era noto, ma
G e mT erano ignoti !
Newton: Metodo per stimare il prodotto
Forza della Terra sulla Luna
FT , L
mT mL
2
=G
=
m
ω
L LdL
2
dL
mm F = −G 1 2 2 u r
r
Isaac Newton
(1642 – 1727)
GmT
2
noti
 2π  3
GmT = 
 dL
 TL 
Legge di gravitazione universale
2
 2π  d L3
g =
 2
T
 L  rT
Calcolo: conferma!
(Inizialmente discrepanze significative…)
Misura diretta di G (Cavendish, 1798)
Qual è il valore di
G?
Bilancia di torsione:
m1
r2
G=
F
m1m2
M = Fl = k0θ
k0θ
F=
l
m2
θ
m2
m1
Verifica misura di θ : rimmuovendo le masse
ristabilire la condizione iniziale
m1
la torsione del filo deve
G = 6.67 ⋅ 10−11 m 3kg −1s −2
Gravitazione
Keplero
I
Newton
Le orbite dei pianeti sono ellittiche,
il Sole occupa uno dei fuochi
III
T 2 = kS a3
F = mω 2 r
F = ma
F1,2 = − F2,1
Newton
mm F = −G 1 2 2 u r
r
Legge di gravitazione universale
Cavendish
G = 6.67 ⋅ 10−11 Nm 2 kg −2 = 6.67 ⋅ 10−11 m 3kg −1s −2
E’ una forza centrale
F = ± F ( r )ur
1. Il momento angolare si conserva
2. La traiettoria si mantiene sullo stesso piano
3. La “velocità areale” è costante Keplero II
4. Forza conservativa
Massa del Sole
Sistema Terra-Sole
mT mS
2
=
m
ω
T T dTS
2
dTS
2
 2π 
= mT 
 dTS
 TT 
3
4π 2 dTS
mS =
G TT2
(III Kelpero!)
4π 2
(1.5 ⋅1011 m)3
=
6.67 ⋅10−11 m3 kg −1s −2 (3.15 ⋅107 s) 2
= 2 ⋅1030 kg
Massa della Terra
Sistema Terra-Luna
3
4π 2 d LT
24
mT =
≃
6
⋅
10
kg
2
G TL
Immagine del Sole ai raggi X
F =G