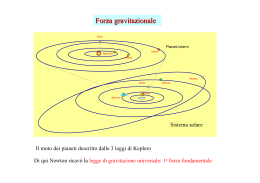
Lezione 6
Forze gravitazionali
Leggi di Keplero
L’ esistenza di una forza gravitazionale tra corpi materiali e’ stata provata in modo indiretto a
partire dallo studio dei pianeti del sistema solare.
• Intorno al 1540 Copernico avanzò l'ipotesi eliocentrica del sistema solare:
• i moti dei pianeti furono oggetto di numerose e accurate misure da parte di Brahe (tra il 1576
e la fine del secolo),
• Keplero formulò tra il 1600 e il 1620, le sue tre leggi.
1) I pianeti percorrono orbite ellittiche intorno al sole che occupa uno dei fuochi
dell'ellisse, figura 11.6a.
2) La velocità areale con cui il raggio vettore che unisce il sole ad un pianeta descrive
l'orbita è costante, figura 11.6b.
3) II quadrato del periodo di rivoluzione di ogni pianeta è proporzionale al cubo del
semiasse maggiore dell'ellisse: T2 = ka3
Deduzione della forza gravitazionale
Le tre leggi di Keplero danno una descrizione puramente cinematica
del moto dei pianeti, ma non descrivono la forza responsabile del
moto. La spiegazione dinamica (ossia la deduzione della forza a
partire dallo studio del moto) fu proposta da Newton nel 1666 e resa
nota nel 1687. Da essa prese corpo la teoria della gravitazione
universale
• Se si assume che le orbite dei pianeti siano circolari (r= cost) e se
la velocità areale è costante, il moto di un pianeta è circolare
uniforme: infatti, per la prima legge di Keplero :
= Cost
ω=
dθ
= ω0
dt
La forza che agisce sul pianeta, e lo forza a percorrere una traiettoria circolare con velocità
costante, deve essere esclusivamente centripeta,
T è il periodo di rivoluzione, m la massa del satellite e r il raggio dell'orbita del pianeta.
• Utilizzando la terza legge di Keplero T2 = kr3 si ottiene:
ossia la forza esercitata dal sole sui pianeti, è inversamente proporzionale al quadrato
della distanza dal sole.
Deduzione della forza gravitazionale
La forza esercitata dal sole sulla terra può quindi essere scritta
e, nell'ipotesi che una formula simile valga per qualsiasi coppia di corpi, la forza esercitata
dalla terra sul sole sarà :
e, per il il principio di azione e reazione
|FTS| = |FST|.
Dall'eguaglianza si ottiene mTkS = mSkT. Definendo la costante
abbiamo per il modulo della forza sole-terra :
(11.3)
E la direzione è quella della retta congiungente il sole alla terra.
Newton ipotizzò che si trattasse di una formula universale ed enunciò la legge di gravitazione
universale:
date due masse qualsiasi, di dimensioni trascurabili rispetto alla distanza mutua, tra di esse
agisce una forza attrattiva diretta lungo la retta congiungente le due masse, il cui modulo
dipende direttamente dal prodotto delle masse e inversamente dal quadrato della distanza.
La costante di proporzionalità γ = 6.67 10-11 m3/kgs2 è una costante universale, che non
dipende dai valori delle masse e dalla geometria del sistema, ma è caratteristica
dell'interazione gravitazionale.
Innumerevoli verifiche sperimentali, soprattutto in campo astronomico, hanno confermato la
correttezza dell'ipotesi. La prima misura diretta della forza di gravità è stata effettuata da
Cavendish nel1798 mediante una bilancia di torsione
Relazione tra costante gravitazionale ed accelerazione di gravità
La (11.3) per un corpo di massa m posto sulla terra, che è un corpo
sferico di massa mT e raggio rT e’:
La formula è valida se si ammette che un corpo a simmetria sferica
eserciti una forza come se la massa fosse tutta concentrata nel suo
centro.
D'altra parte F = mg per cui:
Newton non conosceva né il valore di γ né la massa della terra.
Tuttavia, era noto il periodo di rotazione della luna e una stima
astronomica della distanza terra/luna. Per il sistema terra-luna, si
può scrivere:
per la forza esercitata dalla terra sulla luna, centripeta per la luna;
segue γmT = ωL rL2 = 2π/TL rL2. Dunque dal periodo di rotazione
della luna attorno alla terra ( 29 giorni = 2.36 106s) e dalla distanza
terra-luna,(3.84108m) è possibile determinare il prodotto γmT e
quindi di g.
Al tempo di Newton il valore stimato per la distanza terra-luna era
sbagliato e solo dopo una misurazione astronomica si poté trovare
un buon accordo.
P
Proprietà della forza gravitazionale
r
ur
La forza gravitazionale e’ una forza a lungo range: pur
decrescendo con l’inverso della distanza dalla massa che la
genera, e’ presente in tutto lo spazio. Questo rappresenta una
modifica delle proprietà dello spazio in cui la forza e’ prodotta e si
esprime dicendo che nello spazio e’ presente un campo di forze
E’ una forza centrale: in ogni punto dello spazio la sua direzione
passa sempre per un punto fisso (centro della forza) e il suo
modulo dipende solo dalla distanza dal centro OP = r = F(r)ur.
Corpi soggetti a questo tipo di forze hanno la proprietà di
conservare il momento angolare L.
dL
= r × F = r × F (r )u r = 0 quindi
L = r × mv = Cost
dt
Da questa legge di conservazione deriva la seconda legge di
Keplero. Infatti.
L = r × mv = r × m(v r + v θ ) = r × mv θ
dθ
dθ
2
In modulo ;
L = r ⋅ mvθ = r ⋅ mr
Ossia
r2 ⋅
dt
= r ⋅m
dθ
dA
=2
= Cost
dt
dt
dt
vr
v
vθ
Proprietà della forza gravitazionale
E’ una forza conservativa. Questa e’ una proprietà
comune a tutte le forze centrali. Infatti il lavoro della
forza per uno spostamento da un punto A ad un punto
B dello spazio vale:
B
B
rB
W = ∫ F ⋅ ds = ∫ F (r )u r ⋅ ds = ∫ F (r ) ⋅ dr = f (rB ) − f (rA )
A
A
rA
La forza gravitazionale ha la stessa dipendenza spaziale della forza elettrostatica che e’
alla base della struttura atomica. Questa analogia e’ stata utilizzata, all’ inizio del 900, per
proporre un modello “orbitale” della struttura dell’ atomo che ha dato spiegazione di molti
dati sperimentali ed ha costituito la base della fisica atomica
Energia potenziale gravitazionale
II lavoro compiuto durante lo spostamento ds di una
massa m2 sulla traiettoria nel campo di una massa m1
A
(11.5)
B
II segno negativo indica che la forza gravitazionale è
attrattiva ossia con verso opposto ad u1
il prodotto scalare u1 • ds (figura 11.17), è pari alla
proiezione di ds su u1 e quindi a dr, variazione del
modulo della distanza tra m1 e m2 a seguito dello
spostamento ds. Pertanto
Il lavoro non dipende dalla traiettoria, ma solo dalle
posizioni iniziale e finale,
(11.8)
Energia potenziale gravitazionale
L’ energia potenziale del campo campo gravitazionale si definisce in un modo univoco
in tutto lo spazio assumendo che il suo valore per r→∞ tenda a zero. Dall’ equazione
precedente si ottiene ,
Il valore negativo dell’ energia potenziale indica che e’ necessario compiere un
lavoro contro la forza di gravità per allontanare la massa m2 dalla massa m1
Esempio Due masse ml e mz si trovano a distanza molto grande,
praticamente infinita; la massa m1 è fissa, la massa m2 ha energia
cinetica Ek,in = 1/2 m2v02 Calcolare la velocità della massa quando
è a distanza r da m1
Soluzione L'energia meccanica iniziale del sistema delle due
masse è Em = Ek in = 1/2 m2v02, mentre quando le masse distano r
tra loro l‘ energia meccanica vale:
Eguagliando le due espressioni si trova:
II risultato è vero qualunque sia la traiettoria seguita da m2 nel
campo di m1 perché la forza e’ conservativa
Velocità di fuga dal campo gravitazionale
Calcolare la velocità di fuga di un corpo dalla terra.
Soluzione Nella condizione iniziale abbiamo un corpo di massa m
sulla superficie terrestre, con energia cinetica Ek in = 1/2 mv2. Si
vuole che il corpo arrivi a distanza infinita con velocità v0 > 0.
Scriviamo la conservazione dell'energia meccanica per il valore v0 :
Il valore minimo di v, detto vF, (velocità di fuga), corrisponde a v0 = 0.
Si trova
indipendente dalla massa del corpo. Poiché rT= 6.37 • I06 m,
abbiamo vF= 11.2 km/s = 4 • I04 km/h .
La stessa formula vale per qualsiasi altro pianeta, con gli
appropriati valori di massa e raggio. Nel caso della luna si
trova, per esempio, vL = 2.4 km/s = 8.5 • I03 km/h.
Moti di satelliti
Un satellite di massa m descrive un'orbita circolare di raggio r attorno
ad un pianeta di massa M; con un periodo di rivoluzione T = 2πω.
Calcolare il valore della massa M del pianeta e l'energia del satellite.
Soluzione
La legge di Newton F = ma applicata al satellite si scrive
ossia;
Vediamo che, noto il valore di γ, la massa del pianeta si può dedurre da
misure sul moto del satellite. il risultato non dipende dalla massa del
satellite. ks = T2/r3 è detta la costante del satellite.
L'energia cinetica del satellite è:
L’energia totale del satellite e’
=−
Ep
2
+ Ep =
Ep
2
<0
L’ energia totale del satellite e’ negativa perché l’ energia potenziale (che lega il satellite al
pianeta) e’ maggiore della sua energia cinetica,(che tende allontanarlo). Si dice che il
satellite si trova in uno stato legato. L’ energia Em si dice energia di legame
Moti di satelliti terrestri
Un satellite artificiale di massa m = I03 kg descrive un'orbita circolare intorno alla terra. per
ad un raggio r
Da
con
m2
γ ⋅ mT = 4 ×10 2
s
14
2×107 m
=
r s
Velocità orbitale
Se la velocità del satellite è inferiore alla velocità orbitale, questo percorre una traiettoria
sub orbitale inizialmente di tipo parabolico.
Periodo di rotazione
= 3.14 × 10 −7 r −3 / 2 s
= −2×1014
Energia di legame
17
m
4
×
10
Forza gravitazionale : F = 4 × 10
N
=
r2
r2
14
m
J
2
r
Moti di satelliti terrestri
Per un satellite che orbiti nell’ atmosfera (h < 100 km << rT) si può assumere r ~ rT.. Pertanto:
Un satellite si dice geo-stazionario se percorre la sua orbita in un giorno (
Il raggio dell’ orbita deve essere ::
Ossia ad un’ altezza di circa 36,000 kM dalla superficie terrestre.
)