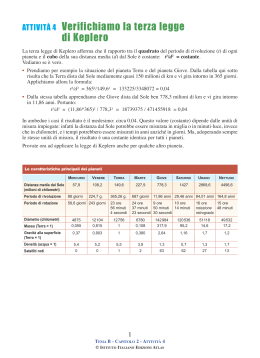
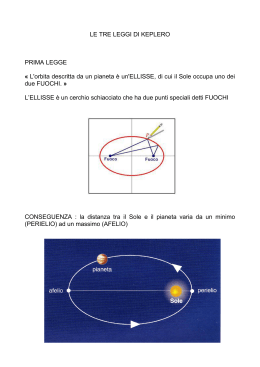
LA LEZIONE: LA LEGGE DI GRAVITAZIONE
Stelle fisse e astri erranti
Oggi, nonostante l’inquinamento luminoso, osservando il cielo notturno privo di nuvole
si riesce a distinguere l’apparizione di Venere (la prima “stella” della sera) e più tardi
quello di gruppi di stelle “fisse” dislocate in posizioni regolari che mantengono
inalterate le distanze relative. Tra le centinaia di oggetti celesti osservabili a occhio
nudo pochissimi mostrano movimenti apprezzabili: il Sole, la Luna e 5 pianeti (Marte,
Mercurio, Venere, Giove e Saturno). L’astronomia matematica (da Tolomeo fino a
Copernico) ha cercato di ridurre il movimento complesso di questi astri erranti a un
insieme di movimenti semplici: circolari e uniformi. Le condizioni particolari del sistema
solare (la massa della nostra stella predominante rispetto a quella dei pianeti, orbite
quasi periodiche e situate all’incirca sullo stesso piano) hanno spinto verso questo
sviluppo. Le possibilità didattiche di un simile approccio non sono però prese in
considerazione per le difficoltà matematiche. Anche se l’utilizzo dei calcolatori ha reso
possibile studiare in modo semplice i movimenti di circoli, a loro volta, mossi da circoli
con movimenti uniformi. Per iniziare dobbiamo però prima ricordare alcune espressioni
relative al moto circolare uniforme e richiamare il concetto antico di deferente ed
epiciclo.
Un moto piano semplice
Un corpo (punto materiale) che si muove lungo una circonferenza con velocità angolare
costante ω a una distanza r dal centro è rappresentato, come chiarito nei testi del
biennio, da un vettore r, avente componenti:
x = r cos(t)
y = r sen(t).
Dal punto di vista fisico ogni componente segue l’equazione caratteristica di un
oscillatore armonico lineare di periodo T = 2p/. L’interpretazione matematica è quella
usuale goniometrica in cui l’angolo descritto dal raggio è uguale a t, rispetto a un
sistema opportuno di coordinate. Ritorniamo al moto dei pianeti.
Moto retrogrado: deferente ed epiciclo
Una delle anomalie delle orbite dei pianeti osservata da Terra è la presenza di moti
retrogradi. Il pianeta si muove per un lungo tratto, diciamo da est verso ovest, e le
osservazioni nei giorni successivi ci portano a ritroso verso est. Un leggero
spostamento che dura un tempo relativamente breve rispetto al periodo di rivoluzione,
per poi ritornare nel giusto verso. In altre parole la traiettoria del pianeta ogni tanto si
interseca formando una serie di nodi. La soluzione adottata dai Greci per spiegare il
moto anomalo è molto semplice. Curve di questo tipo si possono ottenere componendo
due movimenti circolari e uniformi. Il primo, relativo alla circonferenza principale di
rotazione (deferente) e l’altro dovuto all’epiciclo, una rotazione con velocità diversa e
raggio inferiore, il cui centro segue la rotazione del deferente. Proviamo a visualizzare il
modello.
figura 1
Nella figura il deferente ha raggio r1 e l’epiciclo raggio r2. Il movimento in ogni istante
del punto C può essere individuato dalla somma dei vettori AB+BC, le cui componenti
non è difficile vedere sono: x = r1 cos(a) – r2 cos(a) e y = r1 sen(a) – r2 sen(a).1
Programmi per disegnare curve parametriche sono ormai gratuiti ed esistono pagine
web dedicate come http://fooplot.com/
Sostituendo le velocità angolari  la curva viene a dipendere dal parametro tempo
t:
x = r1 cos(t) – r2 cos(tt) e y = r1 sen(t) – r2 sen(tt). Attribuendo dei valori
per tentativi è facile vedere (cambiando le velocità angolari) la composizione dei due
moti con la formazione dei nodi.
Figura 2
Figura 3
Procedendo con più movimenti circolari, la curva può complicarsi variando l’ampiezza
dei nodi come in figura 3. Oggi questi movimenti, non necessariamente periodici, in
meccanica celeste sono chiamati quasi periodici.
Ovviamente cambiando sistema di riferimento dalla Terra (Tolomeo) al Sole
(Copernico) il numero di epicicli da considerare è diverso, ma alcuni movimenti dei
pianeti rimangono assai difficili da descrivere.
1
Sommando le singole componenti del vettore x = r1 cos(a) + r2 cos(a) e y = r1 sen(a) +
r2 sen(a).
Leggi di Keplero
Nella figura che segue è rappresentata l’ellisse2 che descrive l’orbita di Mercurio3,
prendendo come riferimento il Sole.
Figura 4
L’eccentricità del pianeta è quella più grande se confrontata con le eccentricità dei
pianeti conosciuti da Keplero. Eppure la volontà di visualizzare e fissare in modo
inequivocabile la prima legge di Keplero: i pianeti descrivono un’orbita ellittica con il
Sole posizionato in uno dei suoi fuochi, ha generato una forzatura didattica. Così gli
assi dell’ellisse sono in genere rappresentati deformati e la curva nei libri di testo
risulta notevolmente schiacciata. Ritorniamo alla nostra rappresentazione di Mercurio e
disegniamo, a partire dal fuoco, occupato dal Sole, un raggio vettore (con r variabile).
La distanza tra il centro dell’ellisse e il fuoco, piccola per la scala in figura, è pari al
prodotto del semiasse maggiore a per l’eccentricità e.4
Figura 5
Il raggio vettore, che in ogni istante definisce la distanza tra Sole e pianeta, in accordo
alla seconda legge di Keplero, spazza aree uguali in uguali intervalli di tempo. In altre
parole la velocità del pianeta è variabile. Nel punto più lontano dal Sole la velocità del
2
Per disegnare un’ellisse, sempre nella notazione parametrica conviene utilizzare le equazioni:
x = a cos(E), y = b sen (E), con a e b semiassi dell’ellisse. L’angolo E indicato in astronomia come
anomalia eccentrica ha un significato geometrico, al proposito si veda a esempio il libro
http://people.na.infn.it/~covone/astrofisica/fondamenti_meccanica.pdf
3
Se il semiasse maggiore viene posto uguale a 1, quello minore è approssimativamente 0,98.
4
Per trasformare l’ellisse in coordinate polari si pone x = ae + r cos q, y = r sen q
pianeta ha il valore più basso, viceversa nel punto più vicino il valore più alto. La
seconda legge è matematicamente equivalente alla proporzionalità inversa tra distanza
e velocità. Essa deriva dal principio di conservazione del momento angolare. Le prime
due leggi di Keplero sono solo idealizzazioni delle osservazioni astronomiche dei moti
planetari se non integrate con opportune correzioni. L’intuizione di Newton è che la
teoria della gravitazione possa descrivere esattamente le orbite ellittiche dei pianeti
intorno al Sole nell’ipotesi che il moto non dipenda dagli altri pianeti. Torniamo ancora
a Keplero. La terza legge: il quadrato dei periodi di rivoluzione T sono proporzionali al
cubo dei semiassi maggiori a della ellissi percorse dagli astri erranti (T 2=ka3). Abbiamo
già ricordato che trasformare questa figura in una circonferenza non è una forzatura
grandissima. Nel moto circolare uniforme l’accelerazione centripeta 5 è uguale a w2r,
quindi per la seconda legge della dinamica F = m w2r= mr(2p/T)2. La forma della forza
dev’essere in accordo alla terza legge di Keplero6, proporzionale all’inverso del
quadrato della distanza e proporzionale alla massa m del pianeta. Ipotizzando la
completa simmetria tra Sole e pianeta anche la forza di reazione esercitata dal pianeta
sul Sole dev’essere proporzionale alla massa M del Sole. Infine ponendo queste due
forze uguali come intensità si arriva a scrivere per la forza gravitazionale:
F= GMm/r2.
La legge di gravitazione di Newton
Newton nelle dimostrazioni delle conseguenze della legge di gravitazione universale (la
forza agisce tra una mela e la Terra, così come tra la Luna e la Terra) utilizza metodi
geometrici, ma la rapida diffusione della sua teoria è dovuta alla nascente matematica
degli infinitesimi. I pianeti sono così ridotti a punti materiali con la massa concentrata
nei centri. L’effetto gravitazionale su un corpo all’interno della Terra a una distanza r
dal centro, viene a dipendere solo dalla massa della sfera r, in altre parole tutta la
massa della Terra a una distanza maggiore di r, non porta contributi gravitazionali. Le
parabole (caratteristiche dei corpi lanciati dalla Terra), le orbite circolari ed ellittiche
(Luna e pianeti) sono paragonate ed estese all’iperbole, dimostrando che le coniche
sono la forma generale delle traiettorie descritte dall’interazione gravitazionale tra due
corpi. Il peso in prossimità di un pianeta diviene, trascurando la rotazione attorno al
proprio asse, uguale alla forza gravitazionale. Lo sviluppo successivo della meccanica
celeste ha visto soprattutto l’utilizzo di metodi perturbativi. Esistono però soluzioni
particolari del problema di tre corpi interagenti gravitazionalmente che, nati come
curiosità nei lavori di Eulero e di Lagrange, sono oggi applicate al controllo delle sonde
spaziali. Immaginiamo una sonda che si trovi tra la Terra e il Sole, la forza
gravitazionale del Sole supera come intensità quella verso la Terra e l’intensità
risultante è la differenza tra questi due effetti. L’intensità della forza è anche uguale al
prodotto della massa della sonda per l’accelerazione centripeta. Se il periodo di
rotazione della sonda è sincronizzato con quello della Terra i tre corpi possono rimanere
allineati. Basta una piccola deviazione della stazione dal punto di equilibrio perché le
perturbazioni si amplifichino, il valore limitato dell’energia necessaria per correggere
continuamente l’orbita rende comunque questa posizione vantaggiosa. La distanza di
questo punto di equilibrio instabile è di circa un centesimo della distanza Terra Sole 7.
La posizione è chiamata Lagrangiano L1 ed è stata utilizzata in diversi progetti delle
agenzie spaziali. La posizione da molti anni è occupata dalla sonda ACE che studia i
raggi cosmici. Dopo l’opera di Newton, la fisica terrestre e quella celeste sono ormai
definitivamente inseparabili.
5
A esempio approssimando l’orbita della Terra con un raggio costante di circa 1,5 1011 m, si ha una
velocità di circa 3 104 m/s e un’accelerazione verso il Sole di 6 10-3 m/s2.
6
Basta sostituire nell’espressione precedente T2=kr3.
7
Per un calcolo semplice della distanza si veda http://www.phy6.org/stargaze/Ilagrang.htm