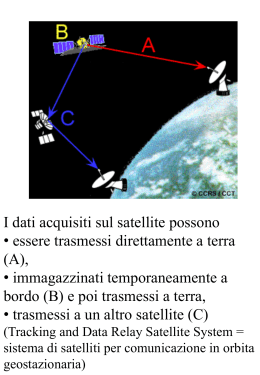
Il satellite SOYUZ VS03 ha come scopo
principale quello di garantire, entro il
2014, un sistema efficiente di navigazione
satellitare in grado di offrire un servizio di
posizionamento globale sicuro: il GPS
europeo.
Questo satellite mira ,come ho già
accennato, alla creazione di 3 servizi:
1. Servizio di base ( «OPEN SERVICE») ;
2. Servizio governativo ( « PUBLIC
RELATED SERVICE»);
3. Servizio di ricerca e salvataggio
(«SEARCH AND RESCUE SERVICE») .
Poniamo caso che si voglia analizzare questo tipo di moto satellitare.. Come procedere?
Se si conosce il periodo di tempo ( vale a dire l’intervallo minimo di tempo affinché un ente
ritorni nella sua posizione di partenza ) , la quota di arrivo raggiunta dal satellite e il
raggio medio della terra , si potrebbero ricavare sia la velocità che l’accelerazione
centripeta del corpo.
Il satellite ,quindi, percorrerà una traiettoria di raggio R:
R = Rt + quota raggiunta dal satellite
Inoltre, sappiamo che il periodo T è …
T= 24ore=86400 s
Dunque, la velocità si ricaverà dalla
applicazione della formula :
La velocità è indipendente dalla massa del satellite ma è influenzata dal raggio dell’orbita ..
Vm= Δs/ Δt = 2∏r / T
.. In cui Δs è lo spazio percorso dal satellite , Δt è l’intervallo di tempo necessario a
percorrere lo spazio ( corrisponde a T ) .
L’accelerazione centripeta ,invece, si ottiene applicando probabilmente:
Ac= 𝑽𝟐 / R
In cui 𝑽𝟐 è la velocità al quadrato, R è il raggio percorso dal satellite .
Inoltre, ipotizzando che il moto in questione sia circolare uniforme, è possibile
calcolare l’ampiezza dell’angolo descritta dal corpo ,se , però, si conoscono gli archi di
circonferenza percorsi dal satellite .
Angolo ἀ= Δl / Δt
Dove ἀ indica l’ampiezza dell’angolo, Δl l’arco di circonferenza percorso e Δt
l’intervallo di tempo impiegato.
NB Gli archi di circonferenza percorsi sono direttamente proporzionali agli intervalli
di tempo impiegati !!
In conclusione, la forza centripeta ( ovvero la forza che costringe il corpo a muoversi
lungo una traiettoria circolare ) sarà uguale all’attrazione gravitazionale della massa
M ( il satellite).