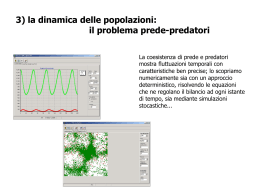
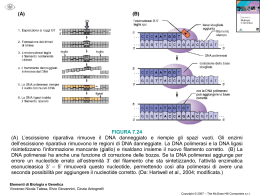
The ultimate goal
“Deciphering” the DNA nucleotide sequence of a living system*.
Tools
…
• information theory
• linguistic analogy
…
• identification of “signal sequence”
…
*It used to be the most difficult macromolecule to analyse. Now it is
possible to determine the nucleotide sequence at a rate of several
hundred nucleotide a day. (August 2005: 1011 bases)
ζ = 0.283
ζ = 0.362
ζ = 0.206
ζ = 0.537
ζ = 0.244
ζ = 0.391
ζ = 0.255
Serie di numeri di diverse origini
Marcata asimmetria in
favore dei digits
bassi nella prima cifra
Legge di Benford
Processi moltiplicativi
Primi 3 digits dei titoli di borsa:
60% 1,2 e 3
40% da 4 a 9
s
t
o
c
k
m
a
r
k
e
t
Invarianza di scala
Soluzione generale: qualsiasi legge di potenza
Distribuzione di probablità dei prezzi delle azioni:
P(N) in una data valuta P(N’) dopo la trasformazione in un’altra valuta
n = primo digit
Funzione decrescente di n
Distribuzione uniforme
nella variabile log N
Legge di Benford
Per α>1 i digit bassi diventano ancora più probabili→ Legge di Benford generalizzata
Due domande
Una delle proprietà matematiche che si applica ad un vasto
numero di fenomeni statistici è il teorema del limite centrale
x1 , x2 , K , x N
Siano un insieme di N (i=1…N) variabili
casuali indipendenti di cui media, µi, e
varianza, σi, esistono e sono finite
S = S ( x1 , x2 , K , x N )
Per esempio
P (S ) =
σ
2
=
N
∑ σ i2
i =1
Per N → ∞ S è distribuita normalmente
S = x1 + x2 + K + x N
1
− ( S − < S > )2
e
2π σ
< S >=
N
∑
i =1
2σ 2
< xi >
Consideriamo una variabile casuale N che cambia nel tempo t con
la legge
N ( t + 1) = N ( t ) + ξ
dove ξ è una variabile casuale
Per t → ∞ la distribuzione P(N, t) → uniforme
Le fluttuazioni sono indipendenti e legate a qualche parametro dinamico esterno
In molti casi, per esempio nel caso dei prezzi delle azioni,
le fluttuazioni
sono invece “relative” al valore della variabile
α>1
1−α N max
N
1−α
N (k )
=
(
1
1−α
N max
− N (k )1−α
1−α
)
1−α
N max
<< N (k )1−α