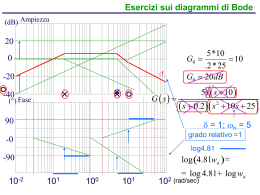
Analisi armonica
Esercitazione
Per un sistema di controllo in retroazione con f.d.t.
Wc=C(s)P(s)/(1+C(s)P(s) definiamo:
modulo alla risonanza del sistema controllato
r
Wc ( jr )
Mr
Wc ( j 0)
è la frequenza in corrispondenza della quale si ha il massimo assoluto di
Poiché per i sistemi controllati a ciclo chiuso
si ha Wc(j0)=1 si usa in genere la definizione
M r Wc ( jr )
W0 ( j)
Analogamente, per i sistemi in retroazione
si definisce Banda passante la pulsazione
alla quale il modulo è attenuato di 3db
rispetto al valore |Wc(j0)|
Diagrammi di Bode
•
•
•
•
•
•
•
•
•
•
•
•
•
>> s=tf('s')
•
>> k=20*log10(10)
Bode Diagram
Transfer function:
10
----s+1
>> bode(g)
Magnitude (dB)
>> g=10/(s+1)
10
0
-10
-20
0
Phase (deg)
Transfer function:
s
20
-45
-90
-2
10
-1
10
0
10
Frequency (rad/sec)
•
•
k=
20
1
10
2
10
Diagrammi di Bode
>> g=10/(s*(s+1))
Bode Diagram
80
Transfer function:
10
------s^2 + s
Magnitude (dB)
60
Phase (deg)
•
•
•
•
•
•
•
•
>> bode(g)
40
20
0
-20
-40
-60
-90
-135
-180
-2
10
-1
10
0
10
Frequency (rad/sec)
1
10
2
10
Diagrammi di Bode
Bode Diagram
>> g=20*(s+2)/((s+3)*(s+1))
Transfer function:
20 s + 40
------------s^2 + 4 s + 3
>> dcgain(g)
30
Magnitude (dB)
•
•
•
•
•
•
•
•
20
System: g
Frequency (rad/sec): 2.01
Magnitude (dB): 16.9
10
0
-10
•
ans =
-20
0
13.3333
•
>> k=20*log10(ans)
•
k=
•
22.4988
•
•
>> bode(g)
>>
Phase (deg)
•
-45
System: g
Frequency (rad/sec): 2
Phase (deg): -52.1
-90
-2
10
-1
10
0
10
Frequency (rad/sec)
1
10
2
10
>> t=[0:0.01:10];
>> in=5*sin(2*t);
>> lsim(g,in,t)
>> plot(in)
>> lsim(g,in,t)
>> bode(g)
>> lsim(g,in,t)
>> 35/5
•
ans =
•
•
7.0
>> 20*log10(35/5)
Linear Simulation Results
50
input
40
output
System: g
Time (sec): 7.48
Amplitude: 35
Input: In(1)
Time (sec): 3.92
Amplitude: 5
30
20
Amplitude
•
•
•
•
•
•
•
•
10
0
-10
-20
•
•
ans =
16.9020
-30
-40
0
1
2
3
4
5
Time (sec)
6
7
8
9
10
>> dcgain(g)
Step Response
14
ans =
10
ans =
13.3333
Amplitude
13.3333
20*2/3
8
6
4
2
0
>> step(g)
System: g
Time (sec): 5.3
Amplitude: 13.3
12
0
1
2
3
Time (sec)
4
5
6
>> g=10/(s^2+1)
Bode Diagram
Transfer function:
10
------s^2 + 1
>> bode(g)
Magnitude (dB)
200
150
100
50
0
-50
-180
Phase (deg)
•
•
•
•
•
•
•
•
-225
-270
-315
-360
-1
10
0
10
Frequency (rad/sec)
1
10
>> t=[0:0.01:10];
>> in=5*sin(2*t);
>> lsim(g,in,t)
Linear Simulation Results
50
input
40
output
30
Amplitude
20
10
0
-10
-20
-30
-40
-50
0
1
2
3
4
5
Time (sec)
6
7
8
9
10
Risonanza
>> in1=5*sin(t);
>> lsim(g,in1,t)
Linear Simulation Results
250
200
150
Amplitude
100
50
0
-50
-100
-150
-200
0
1
2
3
4
5
Time (sec)
6
7
8
9
10
Calcolo di picco di risonanza e banda
passante di un sistema in retroazione
>> g=1/(s*(s+10))
>> w=feedback(100*g,1)
Transfer function:
100
-------------s^2 + 10 s + 100
>> bode(w)
Esercizi proposti
1
• Tracciare i diagrammi di Bode di un
sistema stabile con 2 poli e uno zero
• Simulare la risposta del sistema per un
segnale sinusoidale di ampiezza 10 e
pulsazione 5 rad/sec
• Calcolare il guadagno in continua e
verificare il calcolo tracciando la risposta al
gradino
Esercizi proposti
2
• Tracciare i diagrammmi di Bode di un processo
con un polo stabile ed un polo nell’origine
• Simulare la risposta del sistema per un segnale
sinusoidale di ampiezza 10 e pulsazione 5
rad/sec
• Calcolare il guadagno in continua e verificare il
calcolo tracciando la risposta al gradino
Esercizi proposti
3
• Tracciare i diagrammi di Bode del sistema con funzione
di trasferimento:
• G(s)=10*(s+2)/((s+1)*(s^2+9))
• Simulare la risposta del sistema per un segnale
sinusoidale di ampiezza 10 e pulsazione 5 rad/sec
• Simulare la risposta del sistema ad un segnale
sinusoidale di pulsazione pari alla pulsazione di
risonanza
• Calcolare il guadagno in continua e verificare il calcolo
tracciando la risposta al gradino
Scaricare