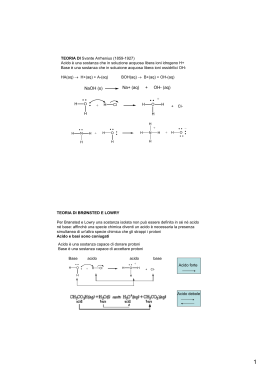
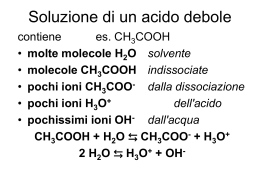
ACIDI, BASI e pH
• Teoria di Arrhenius: sono acide (basiche) tutte
quelle sostanze che, poste in acqua, sono
capaci di dissociarsi formando ioni H+ (OH-).
• Teoria di Brönsted-Lowry: un acido (base) è una
specie che ha tendenza a perdere (acquistare)
un protone.
• Teoria di Lewis: un acido (base) è una qualsiasi
sostanza capace di accettare (donare) una
coppia di elettroni di non-legame
Esempio. Nelle seguenti reazioni, qual è l’acido e quale la base?
NaOH
OH- + Na+
Base
HCl + H2O
Cl- + H3O+
Acido Base
Base
NH3 + H2O
Base
Acido
Acido
OH- + NH4+
Base
Acido
Coppia
coniugata
acido-base
La forza degli acidi e delle basi
forza acida di un qualsiasi acido HA è data dal valore numerico più
o meno elevato della costante di equilibrio della reazione:
[H3O+][A–]
K = ——————
[HA][H2O]
HA + H2O = H3O+ + A–
[H3O+][A–]
K·[H2O] = Ka =—————
[HA]
Ka
costante di dissociazione, o costante di ionizzazione, dell'acido
più elevato è il valore di Ka, più l'acido è forte, più tende a
dissociarsi
più piccolo è il valore di Ka, più l'acido è debole, meno tende a
dissociarsi
esiste una relazione tra la forza di un acido e quella della sua base
coniugata più un acido è forte, più la sua base coniugata è debole e
viceversa
B + H2O = HB+ + OH–
[HB+][OH–]
K·[H2O] = Kb = ——————
[B]
La costante di equilibrio Kb viene definita
costante didissociazione, o costante di ionizzazione, della base
Più elevato è il valore di Kb, più la base è forte
L'autoionizzazione dell'acqua
H2O + H2O = H3O+ + OH–
Acido
Base
[H3O+][OH–]
K = ——————
[H2O]2
a 25 C:
Acido
Base
K·[H2O]2 = Kw = [H3O+][OH–]
prodotto ionico dell'acqua
Kw = [H3O+][OH–] = 10–14
pH
l'inverso del logaritmo della concentrazione molare
degli ioni idrogeno presenti in tale soluzione
pH = –log [H3O+]
pH = –log [H+]
• se pH < 7 acida
• se pH = 7 neutra
• se pH > 7 alcalina (o basica)
il pH può essere rispettivamente minore di 0 o maggiore di 14
• se [H3O+] > 1 M, il pH < 0
• se [OH–] > 1 M, il pH > 14
Appendice: i logaritmi
Si dice logaritmo in base a di un numero x l'esponente y da dare ad a per
ottenere x.
Ovvero se:
x = ay allora y = logax
loga1 = 0
loga(xz) = logax + logaz
loga(x/z) = logax – logaz
logaxk = k logax
Esempio. Calcolare il pK, pH e pOH di una soluzione neutra di acqua a 25 C.
Kw = [H3O+][OH–] = 10–14
pKw = -log Kw = -log (10-14) = 14
Poiché la soluzione è neutra:
[OH–] = [H3O+]
Kw = [H3O+][OH–] = [OH–]2 = [H3O+]2 = 10–14
[OH–] = [H3O+] =
10–14 = 10–7 M
pOH = pH = 7
pKw = -log Kw = -log ([H3O+][OH-]) =
= -log[H3O+] - log[OH-] =
= pH + pOH
Il pH di soluzioni di acidi forti, o di basi forti
pH, di una soluzione di HA con CHA = 0,1 M
H3O+ + A–
HA + H2O
iniziale
finale
0.1
-
-
-
-
-
0.1
0.1
[H3O+] = CHA
pH = –log [H3O+]= –log CHA = -log 0.1 = 1
per soluzioni di acidi forti monoprotici la concentrazione degli ioni
idrogeno è pari alla concentrazione molare dell’acido stesso
pOH, di una soluzione di B di CB = 0,1 M
B + H2O
OH- + HB+
[OH-] = CB
pOH = –log [OH-]= –log CB = -log 0.1 = 1
pH = 14 – pOH = 14 – 1 = 13
per soluzioni di basi forti monoidrossiliche la concentrazione degli
ioni idrossile è pari alla concentrazione molare della base stessa
Calcolare il pH e la concentrazione delle specie ioniche in una soluzione
8,62·10-1 M dell’acido forte HClO4.
HClO4 + H2O
H3O+ + ClO4 –
8,62·10-1 mol HClO4= mol H3O+ = mol ClO4 –
[H3O+] = [ClO4 – ] = 8,62·10-1M
pH = –log [H3O+]= –log (8,62·10-1M) = 0,0645
Il pH di soluzioni di acidi deboli o di basi deboli
pH, di una soluzione di HA, acido debole
Co = concentrazione molare iniziale
HA + H2O
H3O+ + A–
[A–][H3O+]
Ka = —————
[HA]
A equilibrio raggiunto, quali sono le concentrazioni, delle specie
H3O+, A–, HA ?
le possibili fonti di ioni H3O+ sono due:
• la dissociazione dell'acido
• l'autoionizzazione dell'acqua
l’autoionizzazione dell’acqua trascurabile, quindi tutti gli ioni H3O+
presenti in soluzione provengono dalla dissociazione dell'acido
Incognita
[H3O+] = [A–]
[A–][H3O+]
Ka = —————
[HA]
[H3O+]2
————
[HA]
Incognita
1.Considerazione. Ka è “piccola” = la reazione di dissociazione
dell'acido decorre in misura esigua
2. Approssimazione. delle moli iniziali solo una “piccola” parte subisce
ionizzazione, quindi si può approssimare:
[HA]
Ka
[H3O+]2
——————
[HA]
Co
[H3O+]2
————
C0
il pH di soluzioni di acidi deboli
[H3O+]
Ka·Co
pH = 1/2 pKa - 1/2 logC0
Purchè: Ka sia piccola (acido piuttosto debole) e Co grande
(soluzione sufficientemente concentrata), tale che
Ka << C
pOH, di una soluzione di B:
B + H2O
o
OH- + BH+
[BH+][OH–]
Kb = —————
[B]
trascurando gli ioni OH– provenienti dall'autoionizzazione dell'acqua,
[BH+] = [OH–]
dato l'esiguo valore di Kb, si può approssimare che:
[B]equilibrio = Co – [B]dissociata = Co – [BH+]formatosi = Co – [OH–]
[BH+][OH–]
Kb = —————
[B]
[OH–]2
———
[B]
[OH–]2
———
Co
pOH, e quindi pH (pH = 14 - pOH), di soluzioni di basi deboli
[OH–]
Kb·Co
Co
Esempio. Calcolare il pH in una soluzione 1,00 M di acido acetico sapendo che la sua
costante di dissociazione è Ka= 1,85·10–5.
CH3COOH + H2O = CH3COO– + H3O+
[CH3COO–][H3O+]
Ka = ———————— = 1,85·10–5
[CH3COOH]
[CH3COOH]
[H3O+] = [CH3COO–]
Ka
[H3O+]
Ka·Co
[H3O+]2
——————
[CH3COOH]
[H3O+]
Co
[H3O+]2
————
C0
1,85·10–5·1,00 = 0,00430 M
pH = –log [H3O+]= –log (4,30·10-3 M) = 2,366
L’ammoniaca è una base debole con Kb= 1,79·10–5. Calcolare quale concentrazione
deve avere una soluzione di ammoniaca perché il suo pH sia 11,040.
NH3 + H2O = NH4+ + OH[NH4+][OH-]
Kb = —————— = 1,79·10–5
[NH3]
[H3O+] = 10–11,040 = 9,12·10–12 M
[OH–] = Kw / [H3O+] = 1,00 10–14/ 9,12·10-12 = 1,10·10-3 M
[OH–]
Kb·Co
C0
C0
[OH–] 2
——————
Kb
(1,10·10-3 M) 2
—————— = 6,76 ·10-2 M
1,79·10–5