Il seguente materiale NON deve assolutamente sostituire i
libri di testo e/o il materiale didattico indicato dal docente
titolare della disciplina.
Appunti di Dispositivi
Elettronici per i Sistemi
Informativi
Per il Corso di Laurea in Ingegneria
dell’Informazione
Davide SPINOLA
INDICE
-
INTRODUZIONE
-
PARTE 1: CENNI DI MECCANICA QUANTISTICA
-
PARTE 2: TEORIA DELLE BANDE
- Legge di Moore…………………………..…………………………….……….......Pag.5
- Teorema di scalamento a campo elettrico costante……………...……..……….…..Pag.6
- Processi di fabbricazione…….………………….………………………………..…Pag.8
- Costi di fabbricazione…...…………………………………………...….……….….Pag.10
- Riscaldamento dei chip…………………...………………………………….….…..Pag.11
- Energia quanta: effetto fotoelettrico………………………………………….……...Pag.14
- Dualità onda-particella: Ipotesi di De Broglie……………………………..…….….Pag.15
- Il principio di Indeterminazione di Heisenberg……..……………………………....Pag.15
- Equazione d’onda di Schrödinger………….……….........................................….…Pag.16
- Significato fisico della funzione d’onda………..……………………………….…..Pag.18
- Elettrone nello spazio libero………………………………………………………....Pag.19
- Elettrone quasi libero………………...………………………………………….…..Pag.25
- Funzioni di Bloch……………………………………….………..………..……..…Pag.31
- Elettroni e lacune……………………………………………………...……..….…..Pag.40
- Probabilità di occupazione e diagramma a bande di energia…….………….……....Pag.41
- La giunzione pn…………………………………………….……………....………..Pag.43
- La giunzione pn polarizzata………………………………………………………….Pag.45
-
PARTE 3: ETEROSTRUTTURE: QUANTUM WELL, WIRE & DOT
- Eterogiunzioni & eterostrutture…….…………………………..…………………...Pag.49
- Il Quantum Well……………………………………..………………………….......Pag.50
- Il Quantum Wire…………………………………………………….………………Pag.64
- Il Quantum Dot……….. ……………………………………………………………Pag.69
-
PARTE 4: TRANSISTOR A SINGOLO ELETTRONE (SET)
-
PARTE 5: FOTONICA
-
PARTE 6: STRUTTURA LASER A SEMICONDUTTORE
- Il Box a singolo eletttrone…………………………………………………………...Pag.73
- Analisi elettrica del box a singolo elettrone………………………………………....Pag.75
- Transistor a singolo elettrone (SET)………………………………………...………Pag.81
- Il Rates di tunneling…………………………………………..…….…………….…Pag.88
- Applicazioni dei SET nei circuiti logici………………………………….………….Pag.89
- Rete di Pull-Up & Pull-Down in tecnologia SET……...………..…….…….……....Pag.90
- Vantaggi e svantaggi dei SET rispetto ai MOSFET……………………………...…Pag.94
- Guide d’onda ottiche ……………………………………………………...………...Pag.99
- Accoppiatore ottico direzionale curvilineo: Risonatore ad anello………………......Pag.102
- Fisica dei LASER a semiconduttore………………………………………......……Pag.115
- Interazioni di fotoni con atomi……………………………..………..……………....Pag.115
- Semiconduttori a gap diretto e gap indiretto………………………….………...…...Pag.116
- Inversione di popolazione………….………....…………………………………..…Pag.118
- Struttura LASER a semiconduttore: Cavità risonante di Fabry-Perot……………….Pag.118
- Rate Equations dei laser……………………………………………………...……....Pag.129
-
PARTE 7: MODULATORE ELETTRO-OTTICO DI MACH-ZEHNDER
-
PARTE 8: MEMORIE IN SCALA NANOMETRICHE
- L’nterferometro di Mach-Zehnder come modulatore………………………………..Pag.139
- DRAM con materiali ad elevata permettività ………………………………..……...Pag.144
- RAM ferroelettriche (FeRAM)………………………………………………….……Pag.147
2
3
Appunti di DISPOSITIVI ELETTRONICI PER I
SISTEMI INFORMATIVI
Per il Corso di Laurea in Ingegneria dell’Informazione
- INTRODUZIONE -
-
Legge di Moore
La Legge di Moore è una legge empirica che non ha basi statistiche e, pertanto, non è frutto di dimostrazione
bensì essa è una legge che richiede un approccio ‘a posteriori’, cioè che sarà solo dimostrabile nel corso degli
eventi.
La Legge di Moore enuncia:
“La capacità dei processori e/o delle memorie sarà raddoppiata ogni 18 mesi fino al 2015, anno in cui non
si potrà più andare oltre con le prestazioni a causa di un limite di natura fisica.”
Graficamente:
[Chip speed]
2015
[years]
La Legge di Moore, di conseguenza, ha indotto sul mercato un abbattimento dei costi in quanto rappresenta
la continua evoluzione di dispositivi sempre più miniaturizzati.
Difatti, se avessimo un processo di realizzazione a
(anno 2001) è possibile supporre che la
lunghezza di canale di un MOS sia circa pari a
. Con una tecnologia a
(anno 2009) la lunghezza
di un MOS è di
.
Prendendo in considerazione le Equazioni di Poisson:
Dove:
;
Il componente da realizzare viene studiato attraverso queste due equazioni. Nella giunzione
determinare il campo elettrico che si crea si osserva il profilo del drogaggio.
Sapendo che il drogaggio è un termine costante, è possibile esplicitare come il rapporto:
E risolvendo l’Equazione di Poisson attraverso la sostituzione di
elettrico
:
per
nella prima equazione si ricava il campo
4
Sapendo inoltre che:
5
Otteniamo:
Integrando ambo i membri rispettivamente per
ricaviamo:
Si ottiene, in conclusione:
-
Teorema di scalamento a campo elettrico costante
Il campo elettrico
non cambia se, scalando le dimensioni lineari di un fattore , si scalano tutte le altre
dimensioni, compresa la tensione di polarizzazione e, contemporaneamente, la densità di drogaggio di un
fattore .
Prendiamo come riferimento il MOS:
Se volessimo realizzare il MOS a
si deve:
Ma è necessario anche ridurre tutte le altre grandezze di un fattore , come ad esempio la tensione
ampiezze dell’onda in tensione… mentre la densità di drogaggio deve essere scalata di un fattore .
, le
Se si risolve l’Equazzione
nel MOS di partenza e in quello scalato si ottiene lo stesso campo
elettrico
, cioè costante.
L’altro metodo applicabile è quello del potenziale costante, che presenta vantaggi e svantaggi:
- Un MOS realizzato col metodo del potenziale costante risulta essere più veloce (in termini
prestazionali) rispetto a quelli realizzato a campo elettrico costante.
- In questi dispositivi vige il problema dell’elettromigrazione: nelle curve caratteristiche delle porte
elettriche integrate si possono creare negli angoli dei campi elettrici fittizi che, col tempo, rischiano
di degradare il metallo e creare, pertanto, dei cortocircuiti miniaturizzati su porte vicine.
Supponiamo di prendere in considerazione un invertitore CMOS:
Il tempo di carica dipende da:
Con:
.
Dove:
Con:
.
Si nota che nella versione scalata il tempo di carica e di scarica risulta essere più basso rispetto al modello di
default e, pertanto, questo comporta un aumento della velocità (in termini prestazionali) del dispositivo.
6
-
Processi di fabbricazione
Il wafer di silicio si crea con il metodo Czochralski.
Esso consiste in un contenitore contenente, al suo interno, del silicio fuso ove è sovrapposta in maniera
sospesa un’asta che ruota su sé stessa a velocità costante con alla punta un pezzo di silicio puro, detto
Quest’asta entra ed esce, ruotando contemporaneamente, dal contenitore di silicio fuso finché non si ha la
formazione di un cilindro si silicio intorno all’asta, in quanto il seme funge da cristallizzante.
Il cilindro ottenuto verrà, successivamente, sezionato a fette e sottoposto a due processi, chiamati
rispettivamente POLISHING e LAPPING.
Il POLISHING serve a pulire le sezioni ottenute da ulteriori difetti (sbavature) dovuto alla sezionatura
mentre il LAPPING serve a rimuovere i difetti indotti dal POLISHING precedentemente.
7
.
Da ciò viene utilizzato il parametro:
rappresenta la percentuale di chip che risultano funzionanti dal punto di vista
elettrico secondo le regole di progetto.
Le cause di malfunzionamento dei chip possono essere date da difetti durante la mascheratura e la diffusione
oppure per difetti cristallografici. Per evitare questi malfunzionamenti, pertanto, si opera nelle cosiddette
“camere pulite”.
Supponiamo che nel wafer ci siano 4 chip con dei malfunzionamenti di cui non staremo a considerare le
cause. In questo caso la resa in quanto c’è ‘almeno’ un malfunzionamento in ogni chip.
Ma se si riducesse la dimensione del chip, allora altri chip potrebbero trovarsi in un’area del wafer non
affetta da malfunzionamenti e, così facendo, la resa aumenta.
Pertanto, con:
Allora si ha:
8
Dove, nell’ipotesi in cui i difetti fossero nulli
diviene:
E’ opportuno fare presente che la probabilità di poter trovare difetti è data, soprattutto, dal processo di
fabbricazione, ove un processo di fabbricazione più complesso presenterà una probabilità più alta di
comparsa di difetti e, di conseguenza, minor resa.
Graficamente è possibile rappresentare tale caratteristica, nominando con la lettera un processo di
fabbricazione semplice e con la lettera un processo di fabbricazione complesso:
Si esplicita, ora, il parametro:
rappresenta il numero totale di chip realizzati sul wafer.
E’ chiaro che maggiore è l’area
del chip meno se ne possono implementare.
Inoltre se si riduce la dimensione superficiale del wafer la retta di resa geometria si abbassa.
Infine, si elencano gli ultimi tre parametri utili alla fabbricazione di dispositivi miniaturizzati:
rappresenta il rapporto tra numero di piastrine funzionanti dopo la fase
di suddivisione del wafer e il numero di piastrine funzionanti prima di
tale fase.
rappresenta il rapporto tra il numero di piastrine funzionanti dopo la fase di package e
il numero di piastrine iniziali.
-
Costi di fabbricazione
I costi di fabbricazione si dividono in due categorie:
costi di fabbricazione del wafer + costo del controllo della qualità del wafer
costi package + testing finale.
Pertanto, il costo totale
è dato da:
Dove:
.
Il costo totale diviene:
Esplicitando il parametro:
.
Ricaviamo il costo dei singoli chip:
Dove:
Si noti che affinché il valore di diminuisca è indispensabile ridurre opportunamente
e
oppure
aumentare, sempre opportunamente, . Aumentare
significa o aumentare le dimensioni del wafer oppure
9
ridurre le occupazioni di area del chip, di cui entrambi i casi rientrano nella casistica denominata ‘problema
ingegneristico’.
Facendo riferimento alla realtà, in Francia vi è una fonderia che produce wafer ove ha stimato che
aumentando le dimensioni del wafer da
a
vi sono dei vantaggi, i quali sono:
1. Si può rilasciare il controllo di pulizia delle camere pulite e, quindi, la realizzazione di fabbriche a
‘spazio aperto’ con riduzione del numero di filtri che effettuano la pulizia, con conseguente
riduzione dei costi di manutenzione.
2. Il calo del 30% dei costi.
Ovviamente vi sono anche dei svantaggi, i quali sono:
1. Costo del wafer con prezzo che oscilla tra i
e da
. Questo avviene in quanto
su un wafer da
vi sono i processi di polishing e lapping e, soprattutto, il controllo di qualità
della piattezza del wafer stesso, dato che aumentando il diametro aumenta la probabilità che questo
possa flettersi.
-
Riscaldamento dei chip
Consideriamo il seguente schema:
Il chip, riscaldandosi, trasmette calore al substrato e, pertanto, dissipa calore nell’ambiente.
E’ possibile rappresentare quanto detto attraverso la relazione:
E’ possibile rappresentare il tutto attraverso un modello elettrico equivalente secondo la seguente topologia:
Si risolve, ora, il seguente circuito servendoci delle equivalenze ove la potenza dissipata dal calore è
riconducibile ad un generatore di corrente, la temperatura alle tensioni e le resistenze alle resistenze
termiche:
potenza di calore dissipata dal chip;
10
resistenza termica tra la superficie del substrato e la superficie esterna del contenitore;
11
resistenza termica tra la superficie esterna del package e l’ambiente esterno;
temperatura ambiente (supposta costante);
temperatura del chip.
Risolvendo il circuito attraverso le Leggi di Kirchhoff si ottiene:
Sapendo che la temperatura del chip, nel caso peggiore, è pari a circa 150°C e, quindi, anche la potenza
nota così come la temperatura ambiente,
, si ricavano i valori di
e
affinché si possa
dimensionare il package tale da operare a tali temperature:
è
In conclusione, riprendendo in considerazione il postulato della Legge di Moore, è ben chiaro che il limite
fisico che si incontrerà nel 2015 (sotto strette supposizioni) è riguardante proprio il riscaldamento dei chip. In
tempi attuali i chip vengono realizzati con al loro interno ben 55milioni di transistor, comportando già in
queste condizioni un consumo e una dissipazione di calore rilevanti. Vista la continua evoluzione delle
tecnologia sarà dato per scontato che il numero di transistor all’interno dei chip sarà ulteriormente aumentato
ma, al tempo stesso, aumenterà di gran lunga la potenza e la temperatura di esercizio rendendo, così,
inutilizzabili questi dispositivi a temperatura ambiente.
Ed è proprio per questo che si sta’ abbandonando la strada del Silicio effettuando ricerca su nuove possibili
configurazioni e/o tecnologie.
12
Appunti di DISPOSITIVI ELETTRONICI PER I
SISTEMI INFORMATIVI
Per il Corso di Laurea in Ingegneria dell’Informazione
- PARTE 1 –
- CENNI DI MECCANICA QUANTISTICA -
Il movimento di oggetti di grandi dimensioni, come i pianeti e i satelliti, possono essere previsti con un un
alto grado di precisione attraverso la fisica classica che si basa sulle leggi del moto di Newton. Ma alcuni
risultati sperimentali, che coinvolgono elettroni e onde elettromagnetiche ad alta frequenza (in questo caso è
opportuno parlare si grandezze subatomiche), sembrano essere in contrasto con la fisica classica, ovvero non
rispettano le leggi della fisica classica. Tuttavia, questi esperimenti possono dare risultati attraverso i principi
della meccanica quantistica. La teoria della meccanica quantistica ondulatoria è la base per la teoria della
fisica dei semiconduttori.
Nei materiali a semiconduttore le caratteristiche elettriche sono direttamente correlate al comportamento di
elettroni nel reticolo cristallino che compongono il cristallo di semiconduttore. Il comportamento e le
caratteristiche di tali elettroni può essere descritto dalla formulazione della meccanica quantistica detta onda
meccanica.
Prima di approfondire la matematica della meccanica quantistica, ci sono tre principi di cui abbiamo bisogno
di prendere in considerazione: il principio di quanti di energia, il principio di dualità particella-onda ed
infine il principio di indeterminazione.
- Energia Quanta: effetto fotoelettrico
Un esperimento che dimostra una contraddizione tra i risultati sperimentali della teoria classica della luce è
chiamato l'effetto fotoelettrico.
Supponiamo di avere un fascio di luce monocromatica che incide su una superficie pulita di un materiale;
sotto certe condizioni gli elettroni sono emessi dalla superficie.
L'effetto osservato è che ad una intensità costante incidente, la massima energia cinetica
dell’elettrone
varia linearmente con la frequenza, con una frequenza limite
(dove è la frequenza della luce).
Questo risultato è mostrato in figura in basso:
Planck ha postulato nel 1900 che la radiazione termica emessa da una superficie riscaldata sottoforma di
energia discreta è chiamata quanti. L'energia di questi quanti è dato dalla relazione:
Dove la pulsazione è espressa come:
Pertanto si ottiene:
dove è la frequenza della radiazione, è una costante ormai nota come costante di Planck ed, infine, è la
Costante di Planck normalizzata.
Nel 1905, Einstein ha interpretato i risultati fotoelettrici enunciando che l'energia di un'onda luminosa è
contenuta sottoforma discreta di fasci di particelle. Pertanto, la particella come quantità di energia luminosa
si chiama fotone, la cui energia è data anche da
.
13
Un fotone con energia sufficiente relativo al fascio luminoso incidente può rimuovere un elettrone dalla
superficie del materiale.
L'effetto fotoelettrico mostra, pertanto, la natura discreta del fotone e la particella dimostra un
comportamento del fotone.
La massima energia cinetica del fotone per rimuovere un elettrone può essere scritto come:
Dove
è l’energia del fotone incidente mentre
dalla superficie.
è l'energia minima richiesta per rimuovere un elettrone
- Dualità onda-particella: Ipotesi di De Broglie
Abbiamo visto che le onde luminose, attraverso l'effetto fotoelettrico, si comportano come se fossero
particelle. La particella, quindi, ha un comportamento simile a quello delle onde elettromagnetiche.
Nel 1924, De Broglie postulò l'esistenza di onde di materia suggerendo che, poiché le onde di particelle
mostrano un comportamento simile a quello di onde di materia, le particelle potevano mostrare proprietà
ondulatorie.
L'ipotesi di De Broglie era l'esistenza della dualità "onda-particella” da cui deriva il principio di dualità
onda-particella.
La quantità di moto di un fotone è data da:
dove la lunghezza d'onda delle onde di luce. Poi, De Broglie ha ipotizzato che la lunghezza d'onda di una
particella può essere espresso come:
dove
è il modulo (inteso come quantità scalare) del momento della particella e è conosciuta come la
lunghezza d'onda di De Broglie dell'onda materia.
Pertanto, effettuando le sostituzioni, ri ricava la quantità di moto di un fotone espressa in funzione della sua
energia come:
- Il principio di Indeterminazione di Heisenberg
Il principio di indeterminazione di Heisenberg afferma che non è possibile descrivere con assoluta
precisione il comportamento di particelle subatomiche.
1. Il principio di indeterminazione di Heisenber si suddivide in due istruzioni, le quali sono:
E’ impossibile descrivere simultaneamente, con assoluta precisione, la posizione e il momento di una
particella. Se l'incertezza del momento è
e l'incertezza della posizione è , allora il principio di
indeterminazione è indicato come:
con
dove
viene chiamata costante di Planck modificata.
14
2. E’ impossibile descrivere simultaneamente, con assoluta precisione, l'energia di una particella e
l'istante di tempo in cui la particella ha questa energia. Anche in questo caso, se l'incertezza nella
energia è dato dal
e l'incertezza nel tempo è data da , allora il principio di indeterminazione è
indicato come:
Un modo per visualizzare il principio di indeterminazione è considerare la misurazione simultanea di
posizione e momento, e la misurazione simultanea di energia e di tempo. Il principio di indeterminazione
implica che queste misurazioni simultanee sono in errore in una certa misura.
Una conseguenza del principio di indeterminazione è che non possiamo determinare la posizione esatta di un
elettrone.
- Equazione d'onda di Schrödinger
I risultati sperimentali che coinvolgono onde elettromagnetiche e particelle, che non possono essere spiegate
dalle deggi della fisica classica, ha richiesto una formulazione riveduta della meccanica classica.
Schrodinger, nel 1926, avendo recepito il principio di quanti introdotta da Planck e la dualità onda-particella
da De Broglie ha formulato la meccanica ondulatoria, attraverso l’enunciazione dell’Equazione di
Schrodinger.
L’Equazione di Schrodinger è ricavabile attraverso delle “corrispondenze” tra grandezze.
Ipotizziamo di voler determinare l’energia totale del fotone per rimuovere un elettrone dalla superficie di
incidenza; attraverso la meccanica classica possiamo dire che essa è data dalla somma di due contributi
energetici: energia cinetica e l’energia potenziale .
Pertanto, andremo a scrivere:
Sapendo che l’energia cinetica nella meccanica classica è così definita:
Possiamo sostituirla nella espressione energetica totale:
Dalla Fisica Classica sappiamo, anche, che la quantità di moto di un corpo (espressa in modulo) è esprimibile
attraverso l’uguaglianza:
Pertanto, esplicitando la velocità , è possibile affermare:
Sostituendo questo valore nella espressione energetica:
15
La corrispondenza per il ricavo dell’Equazione di Schrodinger è così effettuata:
La meccanica quantistica, quindi, crea una struttura matematica basata sulle Leggi della meccanica classica.
Si noti che all’interno delle parentesi
deve essere inserita la funzione d’onda in riferimento all’elettrone:
Pertanto, effettuando la corrispondenza, otteniamo:
L'Equazione di Schrodinger tempo-variante riferito all’onda tridimensionale, non relativistica, è data da:
dove
è la funzione d'onda tempo-variante,
è la funzione potenziale indipendente dal
tempo, è la massa dell’elettrone e è la costante immaginaria.
L'equazione di Schrodinger è un postulato fondamentale della meccanica quantistica ondulatoria.
La funzione d'onda
viene usata per descrivere il comportamento dell’elettrone matematicamente
e
può essere una quantità complessa.
In condizione di stazionarietà si può determinare la funzione d’onda tempo-invariante semplicemente
attraverso la tecnica di separazione delle variabili: supponiamo che la funzione d'onda tempo-variante può
essere scritta nella forma:
dove
è una funzione della posizione
e
è una funzione del tempo .
Sostituendo questa forma di soluzione nella Equazione d'onda di Schrodinger tempo-variante si ottiene:
Se dividiamo per
, l’equazione diventa:
Il lato sinistro dell'equazione è in funzione della posizione
mentre dal lato destro dell'equazione è
funzione del tempo e dello spazio
.
Il lato destro di questa equazione deve essere pari ad una costante che rappresenta l’energia totale
dell’elettrone:
16
Pertanto si ottiene l’Equazione di Schrodinger tempo-invariante:
Prendendo in considerazione la costante , essa è riconducibile ad una equazione d’onda del tipo:
Risolvendo semplicemente attraverso la tecnica di risoluzione di una semplice equazione differenziale del
primo ordine, la soluzione dell’equazione d’onda
può essere scritta nella forma:
Dove diviene:
con
Sapendo che:
Sostituendo in
diviene:
Pertanto l’elettrone si comporta nel tempo come un’onda avente una pulsazione angolare pari ad
Stare in condizione di stazionarietà significa che l’elettrone nel tempo si comporta come un’onda sinusoidale
di pulsazione .
- Significato fisico della funzione d'onda
Per descrivere il comportamento di un elettrone all’interno di un cristallo ci si serve della funzione d'onda
.
E’ ragionevole chiedersi quale sia la relazione tra la funzione d’onda
e l'elettrone.
La funzione d'onda totale
, ossia tempo-variante, è il prodotto della funzione posizionedipendente e della funzione tempo-dipendente, cioè:
Poiché la funzione d'onda totale
è una funzione complessa, essa non può rappresentare una
quantità fisica reale.
Max Born ha postulato che la funzione
indica la probabilità di trovare la particella
tra e
e in un determinato momento, pertanto:
funzione densità di probabilità
data dal prodotto:
17
dove
è il complesso coniugato di
Effettuando il prodotto della funzione d'onda totale
ha:
così esprimibile:
e il suo complesso coniugato
18
si
Pertanto, abbiamo che:
La funzione densità di probabilità è, pertanto, indipendente dal tempo.
Una grossa differenza tra la meccanica classica e la meccanica quantistica è che in meccanica classica la
posizione di una particella o di un corpo può essere determinato con precisione mentre in meccanica
quantistica la posizione di una particella la si trova in termini di probabilità.
Poiché la funzione
rappresenta la funzione densità di probabilità, per un singolo elettrone
posto nello spazio tridimensionale dato dalle coordinate spaziali
in assenza di forze esterne al sistema
in analisi si deve normalizzare la funzione densità di probabilità per determinare la probabilità di trovare
l’elettrone stesso, vale a dire:
La probabilità di trovare la particella in qualche punto dello spazio tridimensionale è certa.
L’integrale permette di normalizzare la funzione d'onda ed è una condizione al contorno che viene utilizzata
per determinare alcuni coefficienti della funzione d'onda.
- Elettrone libero nello spazio
Consideriamo il moto di un elettrone nello spazio libero monodimensionale, lungo per semplicità di
trattazione. Se non vi è alcuna forza esterna che agisce sull’elettrone (ad esempio un campo elettrico nelle
vicinanze oppure una d.d.p.), allora la funzione potenziale
sarà costante e
, quindi:
L’Equazione di Schrodinger tempo-invariante può essere così scritta:
Ricaviamo dall’operatore Laplaciano:
Mentre l’energia totale della particella:
Otteniamo:
19
Dove:
Risolvendo l’equazione:
La soluzione a questa equazione differenziale può essere scritta nella forma:
Con:
E con:
Effettuando il prodotto scalare tra essi otteniamo:
Dall’algebra vettoriale sappiamo che il prodotto scalare tra versori relativi a piani differenti sono nulli:
Sapendo che il modulo del versore è una quantità sempre unitaria e che l’angolo
zero.
Caso contrario invece:
Pertanto, il prodotto scalare tra il vettore d’onda e il vettore posizione è:
del piano
rispetto
è
Trovandoci in un’analisi unidimensionale lungo , possiamo effettuare l’uguaglianza:
20
Dove, semplificando, si ricava:
Pertanto esplicitando E ricaviamo:
L’autovalore energia E esprime la relazione parabolica che c’è tra il vettore d’onda spaziale
dell’elettrone.
Graficamente è rappresentabile come:
La soluzione dell’equazione d’onda
e l’energia E
diviene:
Dove:
Al determinare l’autovalore energia si ricava l’autofunzione
.
In corrispondenza di una quantità di energia posseduta dall’elettrone c’è un valore del vettore d’onda
corrispondente, positivo.
Pertanto, fissato il valore di
si ha un determinato valore di da cui è possibile ricavare l’autofunzione
.
Ritorniamo, ora, alla soluzione dell’Equazione di Schrodinger tempo-invariante:
Dalle corrispondenze effettuate tra meccanica classica e meccanica quantistica si è eguagliato che la quantità
di moto dell’elettrone, in meccanica classica, è pari a, in meccanica quantistica:
La quantità vettoriale
rappresenta la quantità di moto dell’elettrone, che è così rappresentabile:
Mentre in gradiente:
Sostituendo nella equazione sopra otteniamo:
Effettuando un’analisi monodimensionale (a titolo esemplificativo), possiamo esplicitare il modulo
come:
Pertanto, si ricava che:
Considerando l’autofunzione semplicemente secondo la sola parte diretta per valori positivi di
otteniamo:
Quindi, effettuando le dovute semplificazioni si ha:
Analizzando singolarmente ogni versore associato:
Sommando i termini ottenuti:
In conclusione, possiamo scrivere:
Ed è proprio il momento dell’elettrone libero a spiegare il funzionamento dei laser (che si vedrà più avanti).
L'ipotesi di De Broglie era l'esistenza della dualità "onda-particella” da cui deriva il principio di dualità
onda-particella.
21
Sapendo che la quantità di moto è data anche da:
dove
22
la lunghezza d'onda è esprimibile come:
Pertanto, effettuando le sostituzioni, si ricava che la quantità di moto può essere espressa sia in funzione
della pulsazione che del vettore d’onda spaziale
E quindi, volendo esplicitare il vettore d’onda spaziale
:
Il Valore atteso del momento dell’elettrone libero, definito nelle tre dimensioni, è:
Analizzando solo lungo la componente unidimensionale :
Con:
L’integrale diviene:
Esplicitando nelle tre dimensioni:
23
Appunti di DISPOSITIVI ELETTRONICI PER I
SISTEMI INFORMATIVI
Per il Corso di Laurea in Ingegneria dell’Informazione
- PARTE 2 –
- TEORIA DELLE BANDE -
Introduciamo, ora, le linee basilari della teoria delle bande, che costituisce l’approccio fisico fondamentale
della moderna teoria degli elettroni nei solidi. Questa prende spunto dalla considerazione della periodicità
atomica delle strutture cristalline ed è proprio questa periodicità che porta alla formazione di bande, note
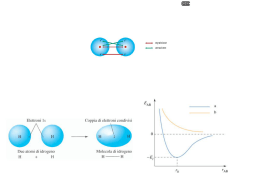
come banda di valenza in cui è più probabile che esista l’elettrone (alla
) e banda di conduzione
dove è più probabile che l’elettrone esista (alla
) entrambe separate da una regione di banda proibita,
chiamata bandgap ove l’elettrone non potrà MAI esistere (per semiconduttori intrinseci).
Un semiconduttore è un solido cristallino o amorfo la cui conduttività elettrica è tipicamente intermedia tra
quella di un metallo e un isolante e può essere cambiata significativamente alterando la temperatura o il
contenuto di impurità del materiale, o mediante illuminazione con luce. Essi assorbono ed emettono fotoni,
subendo le transizioni tra i diversi livelli di energia consentiti, in accordo con la teoria generale
dell’interazione fotone-atomo, presentando delle proprietà che sono uniche per certi aspetti:
1. Un materiale semiconduttore non può essere visto come una raccolta di atomi non interagenti, ciascuno
con i propri livelli di energia individuale. La prossimità degli atomi in un solido rappresentano una serie di
livelli energetici che rappresentano l'intero sistema.
2. I livelli di energia dei semiconduttori assumono la forma di gruppi di livelli ravvicinati che formano
bande. In assenza di eccitazione termica (T = 0 K), questi sono sia completamente occupati dagli elettroni o
completamente vuoti. La massima banda riempita da elettroni viene chiamata banda di valenza, mentre la
banda completamente vuota è chiamata banda di conduzione. Le due bande sono separate da un gap di
energia, chiamato band-gap.
3. Le interazioni termiche e/o ottiche possono impartire energia ad un elettrone, facendolo passare attraverso
il gap dalla banda di valenza alla banda di conduzione (lasciando dietro di sé uno stato vuoto chiamata
lacuna). Il processo inverso può anche verificarsi: un elettrone può decadere dalla banda di conduzione nella
banda di valenza e riempire una lacuna (a condizione che essa è accessibile) per mezzo di un processo
chiamato ricombinazione elettrone-lacuna.
Abbiamo quindi due tipi di particelle che trasportano la corrente elettrica e che possono interagire con i
fotoni: elettroni e lacune.
I dispositivi elettronici, principalmente, fanno uso di silicio (Si) come materiale semiconduttore ma composti
come arseniuro di gallio (GaAs) sono della massima importanza per la fotonica.
-
Elettrone quasi libero
Il più semplice modello consiste nell’introdurre la teoria dell’elettrone quasi libero: in questo caso
l’elettrone risente, seppur debolmente, dell’energia potenziale associata agli ioni nel cristallo.
Poiché gli ioni nel cristallo si ripetono nelle tre dimensioni spaziali
, per semplicità di trattazione si
considererà soloil potenziale periodico nello spazio reale unidimensionale che è rappresentabile nel seguente
modo:
Rappresentazione nello spazio reale
Dove la quantità rappresenta la distanza tra uno ione e l’altro e viene denominato passo reticolare, mentre
viene denominata frequenza reticolare.
Sappiamo che un elettrone libero nello spazio presenta la sua energia nella forma:
24
Consideriamo, ora, gli effetti collegati alla periodicità della struttura cristallina. Gli elettroni, oltre a
comportarsi come particelle discrete, possiedono un carattere ondulatorio (De Broglie). Questa proprietà è
stata già utilizzata nella descrizione degli elettroni liberi, sopra.
Consideriamo un reticolo monodimensionale, con passo reticolare , e immaginiamo di far crescere
lentamente l’energia e corrispondentemente
, attraverso il grafico parabolico. Quando
diventa
abbastanza grande ( abbastanza piccola) l’onda elettronica andrà incontro ad una riflessione di Bragg,
come succede per i raggi X nella identificazione della struttura cristallina in analisi.
Pertanto possiamo enunciare la Legge di Bragg:
“data un’onda elettronica con vettore d’onda ; se quest’onda elettronica interagisce con una struttura
periodica si ha che il vettore d’onda finale
è uguale alla somma del vettore d’onda iniziale con il
vettore reciproco :
Ove il modulo del vettore reciproco
è pari a:
Il vettore reciproco lo si denomina tale, cioè “reciproco”, in quanto dipende dall’inverso del periodo
della struttura periodica, ovvero
.”
Graficamente la Legge di Bragg consiste si una sottrazione vettoriale tra il vettore d’onda finale
vettore d’onda iniziale dando come risultato il vettore reciproco :
Guardando l’energia potenziale in uno spazio reale essa presenta periodicità pari ad
mentre nello spazio ha periodicità pari a
, vale a dire
Graficamente:
Rappresentazione nello spazio reale
, vale a dire
.
e il
25
Rappresentazione nello spazio
Supponiamo di voler applicare la Legge di Bragg nel caso in cui il vettore d’onda finale
opposto al vettore d’onda iniziale :
sia uguale e
Sostituendo tale valore nella equazione appartenente alla Legge di Bragg otteniamo:
Vale a dire:
Il valore del vettore d’onda ottenuto dimostra che ogni qual volta il vettore d’onda iniziale assume come
valore iniziale
si ha condizione di riflessione.
Ponendo
I° ordine:
allora il vettore d’onda inziale varrà
e, pertanto, si è in condizione di riflessione del
Quindi, in una dimensione, i riflessi di Bragg si realizzano quando:
La stessa riflessione di Bragg si verifica quando
da valori superiori. Qualunque tipo di onda
propagantesi in un mezzo periodico subisce lo stesso fenomeno (Brillouin). La figura in basso mostra
l’andamento di contro sia nel caso degli elettroni liberi sia in presenza di un mezzo periodico (cristallo).
26
27
Come vedremo, per
zone o bande distinte.
si determinano gaps di energia dovuti a queste riflessioni. Questi limiti separano
L’intervallo per
prende il nome di prima zona di Brillouin. Esternamente a questa vi è la seconda
zona di Brillouin e così via.
Per meglio capire i gaps di energia, dobbiamo considerare che le interferenze costruttive (le riflessioni) si
verificano per valori di
sia per onde viaggianti verso sinistra
che verso destra
,
presentando un cambio di fase di tra le due onde riflesse dagli atomi.
Le soluzioni per questi valori di sono costituite da uguali componenti di onde viaggianti verso destra,
, e verso sinistra
.
Riprendiamo l’Equazione di Schrodinger riferita all’elettrone libero:
Poiché tutte e due le onde si riflettono sommandosi
e sottraendosi
queste si riflettono, allora le due interazioni possono essere espresse come:
Dalle due interazioni
Dove:
Pertanto si ha:
Graficamente si ottiene:
e
tra loro ogni qualvolta
, pertanto, si viene a formare un’onda stazionaria del tipo:
28
Si noti che l’onda dispari
presenta i massimi tra due ioni mentre l’onda pari
ha i massimi
in corrispondenza dei due ioni, pertanto nella disposizione dispari la probabilità di trovare l’elettrone è tra i
due ioni mentre per l’onda pari la probabilità di trovare l’elettrone è sui due ioni.
A seguito della sua distribuzione, l’elettrone risulterà essere legato al reticolo se si distribuisce come un’onda
pari in quanto essendo vicino agli ioni risente del campo di forze da essi generato, mentre se l’elettrone si
distribuisce come un’onda dispari allora esso si troverà in mezzo ai due ioni non risentendo del loro campo
di forze (anche se esso è presente ma molto debole) e, quindi, l’elettrone è libero di muoversi.
In conclusione si può affermare che in corrispondenza del vettore d’onda iniziale
assumere due livelli energetici possibili.
Graficamente:
l’elettrone può
29
30
- Funzione di Bloch
Un teorema fondamentale che riguarda gli elettroni nei cristalli fu dimostrato da Bloch nel 1928. Questo
stabilisce che le funzioni d’onda degli elettroni nei cristalli devono avere la forma delle funzioni di Bloch:
Il parametro è il vettore d’onda mentre è il vettore posizione. La funzione potenziale periodico del
reticolo
è una funzione periodica di periodo
del reticolo cristallino, ovvero:
Dove
è una qualunque traslazione reticolare. Questa funzione dipende dal vettore d’onda .
Una funzione di Bloch è una funzione d’onda dell’elettrone libero,
, modulata da una funzione che ha la
periodicità del reticolo,
, cioè: un’onda piana modulata.
In una dimensione possiamo scrivere che:
Ovvero, otteniamo:
Con:
Il potenziale periodico del reticolo lo si può esprimere attraverso la Serie di Fourier:
Sapendo che:
31
La Serie diviene:
Pertanto è possibile esprimere ψ(x) come somma di termini dipendenti dalle armoniche del potenziale
Risulta, quindi, che
è un’onda piana modulata per un determinato coefficiente
Esplicitiamo l’Equazione di Schrodinger in forma contratta:
.
Dove:
Che è della forma:
Sostituendo con le Serie ricavate:
Di cui, sviluppiamo matematicamente la derivata parziale rispetto ad
Pertanto, si ha:
del primo termine:
:
Invece, il prodotto del secondo termine:
32
Ponendo che:
Ottengo:
In conclusione, l’Equazione di Schrodinger è così esprimibile:
Dalla condizione della riflessione I° ordine in termini vettoriale:
In modulo si ha:
Sostituisco nell’Equazione di Schrodinger:
Semplificando l’Equazione annullando le sommatorie e i termini esponenziali ricaviamo:
Si vuole, ora, determinare gli autovalori energia
Per convenzione poniamo l’uguaglianza:
Il termine
e i coefficienti in
in modo da poter esplicitare
.
esprime l’energia associata all’elettrone libero della generica onda piana (elettrone che si
muove come un vettore
).
Sostituendo nell’Equazione di Schrodinger si ottiene:
Mettendo in ordine i termini in
:
Esplicitiamo, ora, il Teorema di Bloch il quale enuncia:
“Sia data l’Equazione di Schrodinger con potenziale periodico; la soluzione dell’Equazione di Schrodinger è
data dalla somma di infinite onde piane.
Imponendo questa soluzione si passa da una equazione differenziale ad una equazione algebrica, del tipo:
Dato che l’equazione algebrica presenta infiniti termini non è possibile attuare una risoluzione di questa in
senso assoluto bensì è richiesto l’utilizzo di una risoluzione numerica (computazionale).
Per ovviare alla risoluzione numerica si adottano delle semplificazioni, le quali sono:
1. Ammettere che il potenziale periodico
è dato da un numero finito di armoniche.
Di tutti i valori di
si sceglie una quantità arbitraria che verrà chiamata
e la si
sostituisce nella uguaglianza:
Pertanto, esplicitando
si ha:
L’Equazione algebrica diviene:
Fisicamente significa che la sommatoria delle onde piane non sono indipendenti: la K-esima onda
piana dipende dalla (K-esima - G-esima) onda piana.
Quindi il coefficiente
dipende dal coefficiente
in quanto ogni armonica del potenziale
periodico
influenza tutte le armoniche delle onde piane.
2. Possiamo rappresentare il potenziale periodico con solo l’armonica “dominante”, ovvero dove si
forma il band-gap al valore di
corrispondente a
.
Quindi, sostituendo nelle equazioni algebriche e mettendole a sistema ricaviamo:
33
Supponiamo che il potenziale periodico sia pari:
Poiché il band-gap si crea ha quando |
, con
34
, ci poniamo nella condizione in cui:
Ovvero:
Sostituendo nel sistema con
si ha:
Poiché, attraverso una “forzatura” si ha che:
Il sistema diviene:
Ovvero:
Le due soluzioni del sistema rappresentano l’energia dell’elettrone libero in corrispondenza del
bordo-banda.
Si vede che
assume due valori in corrispondenza del bordo-banda pertanto si è dimostrato,
matematicamente, che si crea il band-gap la cui ampiezza è pari a due volte
Effettuando un’analisi generalizzata, si pone:
.
Il sistema diviene:
35
In forma matriciale:
Risolvendo l’equazione di secondo grado in
:
Le energie dell’elettrone libero in corrispondenza del bordo-banda, nel caso generalizzato, sono:
Adesso si vuole determinare il come si presenta il profilo delle bande in corrispondenza del bordobanda.
Poniamo che il vettore:
Ovvero il termine indica che vi è uno spostamento dal bordo-banda di una quantità pari proprio a
.
Ritornando al sistema ricaviamo:
Che in forma matriciale diviene:
Effettuando il prodotto algebrico tra le due parentesi si ricava un’equazione di secondo grado
espressa in
:
Si noti che si è ritrovata un’altra equazione di secondo grado espressa in
possiamo esprimerla come:
In conclusione:
Ritornando all’equazione espressa in
I possibili valori di
, il delta è così esprimibile:
(radici dell’equazione) sono:
. Risolvendola
36
Mentre la larghezza del bandgap è approssimabile:
Attraverso una ‘forzatura’ è possibile eguagliare:
Otteniamo:
Sapendo inoltre che:
Sostituendo a
Otteniamo:
il valore posto in precedenza:
37
Graficamente:
Si definisce
la regione spaziale compresa nell’intervallo spaziale –
Il diagramma a bande viene disegnato, ora, shiftando le curve di
congiuntenti all’origine:
38
.
Si introduce, ora, il concetto di
intesa come una carica positiva
ove la sua energia è:
Il diagramma a bande visto come elettrone-lacuna è così rappresentato:
Banda di conduzione relativa all’elettrone
Banda di valenza relativa alla lacuna
Si noti che il diagramma a bande è composto da due archi di parabola invertiti tra loro di cui vengono
descritti per piccoli valori di
cambiando la massa a riposo nella relazione:
Sostituendo al valore di i valori di massa effettiva dell’elettrone
(in funzione del materiale in esame) si ricava:
e di massa effettiva della lacuna
39
- Elettroni e lacune
Nei semiconduttori elementari, quali Si (silicio) e Ge (germanio), ci sono quattro elettroni di valenza per
atomo, la banda di valenza ha un numero di stati quantici tali che in assenza di eccitazioni termiche la banda
di valenza è completamente riempita e la banda di conduzione è completamente vuota; di conseguenza, il
materiale non può condurre l'elettricità.
Con l'aumento della temperatura, tuttavia, alcuni elettroni saranno eccitati termicamente tali da oltrepassare il
bandgap e arrivare alla banda di conduzione dove, essendo vuota, si trova una grande varietà di stati non
occupati (vedi sotto).
Questo processo, svolgendosi in tutto il reticolo cristallino e supponendo l’applicazione di un potenziale
elettrico esterno, contribuisce nel generare una corrente elettrica. Inoltre, la migrazione di un elettrone dalla
banda di valenza genera uno stato vuoto quantico (lacuna), consentendo ai restanti elettroni nella banda di
valenza di scambiare posti tra loro sotto l'influenza di un campo elettrico.
Questo processo può essere considerato, nel suo complesso, come il movimento, nella direzione opposta agli
elettroni, di posti lasciati vuoti; cioè la lacuna si comporta come se si dispone di una carica positiva.
Il risultato di ogni elettrone eccitato è, quindi, la creazione di un elettrone libero nella banda di conduzione e
una lacuna libera nella banda di valenza. I due portatori di carica sono liberi di deriva sotto l'effetto del
campo elettrico applicato e per generare così una corrente elettrica. Il materiale si comporta come un
semiconduttore la cui conduttività aumenta rapidamente con la temperatura.
40
-
Probabilità di occupazione e diagramma a bande di energia
In assenza di eccitazione termica (T = 0 K), tutti gli elettroni occupano i livelli più bassi di energia possibili.
La banda di valenza viene poi riempita completamente dagli elettroni (non ci sono buche) e la banda di
conduzione è completamente vuota (non contiene elettroni, però è piena di lacune).
Quando la temperatura viene aumentata, l’eccitazione termiche è tale da sollevare alcuni elettroni dalla
banda di valenza alla banda di conduzione, lasciando così degli stati vuoti nella banda di valenza (forilacune). Le leggi della meccanica statistica impongono che in condizioni di equilibrio termico a temperatura
T, la probabilità che un dato stato di energia è occupata da un elettrone è determinato dalla funzione
Fermi:
dove
è la costante di Boltzmann e
è una costante nota come Energia di Fermi o livello di Fermi.
La Funzione di Fermi è anche nota come Distribuzione Fermi-Dirac.
Il livello di energia
può essere occupato da un elettrone [con probabilità
]:
Il livello di energia
può essere occupato da una lacuna [con probabilità
]:
La funzione
non è essa stessa una distribuzione di probabilità piuttosto è una sequenza di probabilità di
occupazione di livelli di energia successivi.
Poiché
qualunque sia la temperatura T, il livello di Fermi è il livello di energia per cui la
probabilità di occupazione sarebbe ½.
La funzione di Fermi è una funzione monotona decrescente di (vedi figura sotto).
Analizziamo la Funzione di Fermi nei seguenti casi:
1. Allo zero assoluto si ha che
e nella condizione in cui
: la quantità esponenziale
tenderà ad infinito (positivo) e, pertanto, la funzione
sarà pari a zero. Questo dimostra che la
probabilità di trovare l’elettrone è nulla.
41
2. Allo zero assoluto si ha che
e nella condizione in cui
: la quantità esponenziale
tenderà ad infinito (negativo) e, pertanto, la funzione
sarà pari all’unità. Questo dimostra che
la probabilità di trovare l’elettrone è massima, ovvero al 100% (o per meglio dire – con certezza).
Alla temperatura
si ha che
, pertanto:
per
e
per
.
Questo stabilisce il significato di , che è la divisione tra i livelli energetici occupati e non occupati a T =
0K.
Poiché
è la probabilità che il livello di energia
sia occupato da un elettrone mentre
è la
probabilità che
sia occupata da una lacuna, è possibile riassumere come:
= probabilità di occupazione di un elettrone (Banda di Conduzione)
= probabilità di occupazione di una lacuna (Banda di Valenza).
Queste funzioni sono simmetriche rispetto al livello di Fermi.
La figura sopra mostra la funzione di Fermi
e la probabilità che il livello di energia
è riempito con
un elettrone mentre
è la probabilità che il livello di energia
sia riempito con una lacuna.
Nella banda di valenza,
è la probabilità che il livello di energia
è occupata da una lacuna.
A
,
per
e
per
cioè, non ci sono elettroni nella banda di
conduzione e lacune nella banda di valenza.
3. Nella condizione in cui
, ponendo a
un qualsiasi valore, si ha che l’esponenziale tenderà
all’unità e, pertanto, la funzione
sarà pari ad un mezzo. Questo dimostra che la probabilità di
trovare l’elettrone è al 50%.
Nella realtà non è possibile trovare l’elettrone nella regione di band-gap e, pertanto, è possibile ottenere
risultati concreti per valori energetici maggiori di
e minori di .
E’ possibile tracciare il diagramma a bande in funzione della posizione attraverso i livelli energetici di
conduzione e valenza
e :
42
Dove si esplicitano:
Livello energetico che presenta l’elettrone all’infinito (nella condizione in cui questo non è legato ad
alcun reticolo);
Affinità elettronica;
Livello energetico di Fermi-intrinseco posto, come riferimento, a metà del band-gap;
Funzione lavoro.
Le regole per tracciare il diagramma a bande sono le seguenti:
1. Il livello
deve essere una curva continua;
2. L’affinità elettronica e il bandgap sono caratteristiche del reticolo cristallino e, quindi, devono
assumersi costanti dipendentemente dal materiale in esame.
Queste due condizioni implicano, pertanto, che sia che
siano costanti.
-
La giunzione pn
La giunzione pn è una omogiunzione (in quanto il substrato è in silicio) tra un semiconduttore di tipo p ed un
semiconduttore di tipo n. Esso agisce come un diodo che può servire in elettronica come raddrizzatore, porta
logica, regolatore di tensione (diodo Zener), e in optoelettronica come un diodo emettitore di luce (LED),
diodo laser, fotorivelatore, e cella solare.
Una giunzione pn consiste nel contatto metallico di due semiconduttori drogati di tipo p e di tipo n,
rispettivamente l’uno con l’altro.
La regione di tipo p ha un'abbondanza di lacune (portatori maggioritari – carica positiva ) e pochi elettroni
mobili (portatori minoritari), mentre la regione di tipo n essendo composta ha un'abbondanza di elettroni e
lacune pochi mobili (portatori maggioritari – carica negativa ) (vedi figura in basso).
Entrambi i portatori di carica sono in continuo movimento in tutte le direzioni per eccitazione termica.
Quando le due regioni vengono portate a contatto (vedi la figura in basso), hanno luogo i seguenti fenomeni:
1. Gli elettroni e le lacune si diffondono da zone ad alta concentrazione verso zone a bassa
concentrazione. Questo processo prevede che gli elettroni passino dalla regione n alla regione p
lasciando così (nella regione n) gli atomi donatori di carica positiva ionizzati di loro appartenenza;
quando questi giungono nella regione p si ricombinano con le lacune che, in questa regione,
abbondano.
Analogamente, le lacune diffondono dalla regione p alla regione n lasciando così gli atomi accettori
di carica negativa ionizzati di loro appartenenza. Pertanto, nella regione n le lacune si ricombinano
con gli elettroni mobili.
43
2.
3.
4.
5.
6.
7.
Dato che questo processo di diffusione non può durare all’infinito vi è una rottura dell’equilibrio di
carica tra le due giunzioni.
Come risultante del processo di diffusione si viene a formare una regione stretta su entrambi i lati di
contatto delle regioni n e p (giunzione) ove i portatori di carica sono nulli. Questa regione prende il
nome di strato di esaurimento dove sono presenti solo gli ioni fissi (ioni positivi nella regione n
privi di elettroni di valenza e ioni negativi nella regione p privi di lacune).
Lo spessore di tale strato in ciascuna regione è inversamente proporzionale alla concentrazione dei
droganti nelle regioni stesse.
Le cariche fisse situate nello strato di esaurimento creano un campo elettrico che punta dal lato n
verso il lato p della giunzione. Questo campo interno prende il nome di built-in in quanto ostacola la
diffusione di ulteriori portatori mobili (elettroni e/o lacune) attraverso la giunzione.
In condizione di equilibrio si stabilisce una d.d.p. tra i due lati dello strato di esaurimento, ove il
lato n presenta un potenziale maggiore rispetto il lato p.
Il built-in fornisce una energia potenziale più bassa per un elettrone sito nella regione n rispetto alla
regione p; pertanto, le bande di energia risulteranno piegate.
In equilibrio termico vi è una sola funzione di Fermi per l’intera struttura in modo che i livelli di
Fermi delle regioni p e n siano allineati.
Non vi sono flussi netti di corrente che attraverso la giunzione.
44
-
La giunzione pn polarizzata
Un potenziale applicato esternamente alla giunzione pn altererà la differenza di potenziale tra le regioni p ed
n. Ciò, a sua volta, modifica il flusso dei portatori di maggioranza in modo che la giunzione può essere
utilizzata come "gate".
Se la giunzione viene "polarizzata direttamente", applicando una tensione positiva
alla regione p (vedi
figura in basso), il suo potenziale viene aumentato rispetto alla regione n; in questo modo la presenza della
tensione di polarizzazione esterna determina un allontanamento dall'equilibrio e un disallineamento dei
livelli di Fermi nelle regioni p ed n, così come nello strato di esaurimento.
La presenza di due livelli di Fermi nello strato di svuotamento,
e
, rappresenta uno stato di quasiequilibrio.
Poiché in un semiconduttore drogato di tipo si ha maggioranza di elettroni, la probabilità di trovare questi
in una banda di conduzione
è maggiore e, pertanto, il livello di Fermi-intrinseco
si alza rispetto ad un
semiconduttore drogati di tipo , ove si ha maggioranza di lacune e la probabilità di trovare gli elettroni in
una banda di conduzione è molto bassa, così come il livello di Fermi-intrinseco si abbassa.
Attraverso il diagramma del bordo-banda si noti che:
Figura 0
45
46
Figura 1
Figura 2
Si noti dalla rappresentazione grafica, sopra (figura 0), che per il lato drogato di tipo si ha che il livello
energetico di Fermi-intrinseco
è minore della quantità energetica di gap pari a
, pertanto ci
troviamo nella condizione in cui è possibile effettuare l’approssimazione:
.
La funzione distribuzione di Fermi ci darà un valore tale da determinare la probabilità di trovare l’elettrone.
In questo caso, nell’ipotesi in cui
Si è dimostrato che, nella regione , la probabilità di trovare l’elettrone è pressoché nulla. Questo è in linea
sul fatto che la regione trivalente presenta un eccesso di lacune, e no di elettroni.
Si noti, ora, che per il lato drogato di tipo si ha che il livello energetico di Fermi-intrinseco
è maggiore
della quantità energetica di gap pari a
, pertanto ci troviamo nella condizione in cui è possibile
effettuare l’approssimazione:
.
La funzione distribuzione di Fermi ci darà un valore tale da determinare la probabilità di trovare l’elettrone.
In questo caso, nell’ipotesi in cui
Si è dimostrato che, nella regione , la probabilità di trovare l’elettrone è (quasi) massima. Questo è in linea
sul fatto che la regione pentavalente presenta un eccesso di elettroni, e no di lacune.
Di conseguenza, se polarizzassimo il semiconduttore attraverso una polarizzazione di tipo “diretta”, la
barriera di potenziale andrebbe sempre più a portarsi a livello fino ad un livello energetico di Fermi in linea
con la metà del livello energetico di gap, come mostra la figura 1 sopra. Questo “livellamento” permette la
conduzione di corrente.
Caso inverso, invece, attraverso una polarizzazione di tipo “indiretta” si ha un aumento della barriera di
potenziale tale da impedire la conduzione, come mostrato in figura 2.
47
48
Appunti di DISPOSITIVI ELETTRONICI PER I
SISTEMI INFORMATIVI
Per il Corso di Laurea in Ingegneria dell’Informazione
- PARTE 3 - ETEROSTRUTTURE: QUANTUM WELL, WIRE & DOT -
-
Eterogiunzioni & Eterostrutture
La eterogiunzione è una giunzione tra materiali aventi gap energetici diversi. La eterogiunzione presenta,
inoltre, differenti barriere di potenziale per gli elettroni e per le lacune, al contrario delle omogiunzioni.
Due semiconduttori dissimili con band-gaps differenti uniti per formare una etero giunzione.
Le eterostrutture sono formate da multiple eterogiunzioni.
Se uno strato sottile di un materiale a bandgap-stretto, chiamato “A”, viene interposto a sandwich tra un
materiale a largo-bandgap, chiamato “B”, allora si ottiene una doppia eterogiunzione come mostrato in
basso:
Se il livello “A” è sufficientemente sottile per le proprietà quantistiche, allora tale disposizione dei gaps
prende il nome di singolo quantum well, che significa in italiano singola buca quantica.
49
Se nel sistema sono presenti i portatori di carica mobili (elettroni e lacune), sia termicamente (come prodotto
intrinseco) o per dopaggio (come prodotto estrinseco), allora essi tenteranno di abbassare le loro energie.
Pertanto, in questo esempio, gli elettroni (che vengono riconosciuti come i cerchi neri – pieni) che si trovano
inizialmente nella banda di valenza e le lacune (che vengono riconosciuti come i cerchi bianchi – vuoti) che
si trovano inizialmente nella banda di conduzione si ricombineranno nel quantum well in modo da diffondere
gli elettroni nella banda di conduzione e le lacune nella banda di valenza.
La struttura rappresentata sopra appartiene al sistema del 1°-tipo; in questa tipologia il bandgap di un
materiale (A) si trova interamente all’interno del bandgap del materiale avente bandgap più ampio (B), così
entrambi i portatori mobili sono localizzati nella stessa regione dello spazio per rendere più efficiente
(veloce) la ricombinazione.
Un esempio strutturale di eterostruttura quantica nelle tre dimensioni è:
Per creare le eterostrutture si adotta un processo tecnologia denominato
dove richiede che i
parametri reticolari siano uguali tra loro altrimenti non si crea il legame tra le celle e non avviene
l’accrescimento di un materiale sull’altro. Il bandgap della lega
) aumenta all’aumentare del
dell’arseniuro di gallio (cioè la concentrazione molare di
nella lega) rispetto all’
-
Il Quantum Well (Buca Quantica)
Consideriamo una eterostruttura avente la seguente condizione:
Una struttura avente questa caratteristica prende il nome di Quantum Well.
Graficamente:
50
Mentre il diagramma a bande è il seguente:
Per studiare un dispositivo di questo tipo ci si serve dell’Equazione di Schrodinger.
Si noti che l’elettrone oltre a risentire dei potenziali periodici dei reticoli dei due materiali risente anche del
potenziale della barriera, pertanto bisognerà aggiungere all’operatore Helmitoniano anche il potenziale della
barriera
.
Il problema di trattazione si risolve imponendo che l’elettrone abbia nella buca la massa effettiva in banda di
conduzione dell’
e nelle altre zone al di fuori della buca la massa effettiva in banda di conduzione
dell’
.
Indichiamo con
il potenziale della barriera che si distribuisce nel seguente modo lungo la posizione :
Si ipotizzi che le barriere sono semi-infinite, cioè che la buca di potenziale presenti un valore no infinito
bensì un valore finito pari a .
Possiamo passare, ora, a scrivere l’Equazione di Schrodinger indicando con
la massa effettiva
dell’elettrone, cioè:
L’Equazione di Schrodinger in forma contratta è della forma:
51
Dove, esplicitando l’operatore hamiltoniano diviene:
52
Si osservi che la struttura è traslazionalmente invariante nella direzione e , cioè che effettuando una
traslazione arbitraria lungo e y le proprietà chimico-fisiche non cambiano.
Di conseguenza, l’invarianza traslazionale lungo una direzione si traduce, matematicamente, nel separare le
variabili nell’equazione differenziale:
Pertanto, sostituendo nell’Equazione di Schrodinger otteniamo:
Ora, considerando le equazioni differenziali rispetto
e z ricaviamo:
Si noti che le equazioni di differenziali rispetto ed sono proprio le Equazioni di Schrodinger nel caso di
un elettrone libero avente massa effettiva
, difatti risolvendole si ricavano gli autovalori energia
dell’elettrone stesso lungo e :
Quindi, sapendo che l’autovalore energia nelle tre direzioni
di rispettivamente lungo
, allora si può scrivere:
Dove, dall’algebra vettoriale si sa che:
Quindi si ottiene:
è dato dalla somma dei singoli contributi
Dove:
53
Con:
Pertanto si può affermare che l’elettrone è libero di muoversi in banda di conduzione come se fosse un
‘elettrone libero’ avente massa effettiva e l’andamento è un moto parabolico e continuo e ad ogni valore di
corrisponde un valore di
.
Ora consideriamo la componente lungo
Dove, suddividendo in intervallo spaziali possiamo distinguere il well e le barriere:
Si ha che il potenziale
è simmetrico per riflessioni, del tipo
, e pertanto:
Quindi nel well l’autofunzione
non sarà un’onda piana che si propaga (come nel caso delle direzioni e y
) in quanto l’onda nel well non ha la possibilità di spaziare lungo z perché incontrando le due barriere essa
viene riflessa.
Pertanto l’autofunzione
nel well, cioè in
, si presenterà come un arco di funzione
trigonometrica che è la combinazione di
Considerando la regione well:
e
.
L’autofunzione in
è pari a:
54
Dove, si esplicitiamo:
Per la simmetria del potenziale, pertanto, le autofunzioni sono a parità pari e a parità dispari:
Per gli stati confinati al pozzo, l'energia deve essere inferiore alla barriera di altezza
riorganizzare l'equazione di Schrödinger per la barriera di destra:
, in modo da
Risolvendola:
Otteniamo:
Con:
Queste condizioni al contorno per gli stati confinanti il pozzo (well) sono indicate come le condizioni al
contorno standard.
Prendendo in considerazione la funzione pari della soluzione generale dell’Equazione di Schrodinger
nell’intervallo
si può scrivere:
Queste funzioni d'onda sono reali e le autofunzioni di questo sistema confinato non conducono corrente e
quindi sono indicati come stati stazionari.
Utilizzando queste forme processuali della funzione d'onda nelle loro equazioni di Schrödinger
corrispondenti, si ha:
è l’autovalore di energia comune nelle due equazioni ma è indispensabile determinare una equazione che
permetta di determinare propriamente . Questa equazione la si ottiene imponendo le condizioni di
continuità delle funzioni
e della sua derivata prima:
Si consideri l'interfaccia in
Eguagliando le due espressioni di
Derivando ambo i membri per :
si possono esprimere le due equazioni:
si ottiene:
55
Ovvero:
56
Mettendo a rapporto l’equazione (1) con l’equazione (2):
Cioè:
In conclusione:
Ribaltando la funzione si ottiene:
Analizzando ora per
si noti che si ottiene la stessa funzione ricavata sopra:
Effettuando gli stessi procedimenti adottati prima si ricava:
Prendendo, ora, in considerazione la funzione dispari della soluzione generale dell’Equazione di Schrodiger
per l’intervallo
si ha:
Considerando l’interfaccia in
ricaviamo:
57
Eguagliando le due equazioni:
Derivando ambo i membri rispettivamente per :
Diviene:
Dividendo rispettivamente la funzione (1) per la funzione (2) otteniamo:
Cioè:
Quindi:
Ribaltando la funzione si ha:
Ricordando che sia
di .
che
sono funzioni dell’energia
, allora anche le equazioni
e
sono funzioni
Pertanto, ricapitolando, si sono ricavate le Equazioni Trascendenti (non hanno soluzioni in forma chiusa):
Sapendo che:
Attraverso l’iterazione di Newton-Raphson è possibile determinare, approssimativamente, i valori in modulo
di :
Si dimostra che il numero delle soluzioni per le funzioni pari
e dispari
è discreto:
All’interno del Well, al suo interno, i livelli di energia si distribuiscono nel seguente modo:
I livelli di energia (riferito in numero di livelli) dipende dall’altezza e larghezza del well.
E’ evidente che la prima soluzione pari è minore rispetto alla prima soluzione dispari,
.
Quando l’elettrone è nel well si distribuisce su un livello discreto di energia; da qui deriva il nome
“Quantum Well”, ove si evince che l’elettrone risiede su livelli quantizzati di energia.
58
Se andiamo a diagrammare la funzione
fissando i valori di energia otteniamo:
Rappresentando globalmente:
Se volessimo determinare la costante per la funzione
riferita al Quantum Well appena trattato,
dobbiamo imporre la condizione di normalizzazione che consiste nel seguente procedimento.
Prendiamo in considerazione la funzione a simmetria pari:
59
Effettuando il modulo quadro si ricava la funzione densità di probabilità:
Dove, dalla goniometria, il coseno quadro è esprimibile anche come:
Pertanto, otteniamo:
Sappiamo che la probabilità di trovare l’elettrone nel well è certa:
Pertanto, sostituendo nell’integrale la funzione densità di probabilità otteniamo:
Pertanto, esplicitando :
Sostituendo
nell’autofunzione
Quindi, in conclusione:
si ha:
60
Ritorniamo, ora, al quantum well e sappiamo che l’autovalore energia è esprimibile come:
E’ importante notare che i due autovalori energetici
e
non hanno lo stesso significato fisico in quanto
l’autovalore energia
si presenta sottoforma di livelli quantizzati di energia.
Pertanto nelle strutture quantum well gli elettroni presentano un’energia quantizzata nel well,
,e
una energia da elettrone quasi libero nella banda di conduzione.
Quindi nel well l’elettrone si muove liberamente sul piano
mentre lungo si posiziona su livelli
quantizzati di energia. A causa di ciò il quantum well viene definito a dimensionalità 2D.
Ora consideriamo un caso particolare: una buca quantica infinita (infinite quantum well)
E’ evidente che la probabilità di trovare l’elettrone nella barriera è nulla in quanto essa è infinita.
Al di fuori del well,
, e quindi l'unica soluzione possibile è
, che a sua volta implica che tutti i
valori di energia
sono consentiti.
All'interno della buca di potenziale di ampiezza , l'equazione di Schrodinger si semplifica in:
61
Il che significa che la soluzione di
è:
62
L’autofunzione è:
Mentre l’autovalore energia è:
Verificando le condizioni al contorno per la buca quantica infinita ricaviamo che:
Pertanto studiando l’autofunzione ricavata dall’Equazione di Schrodinger nella buca quantica infinita
possiamo esplicitare il valore di :
Per
sappiamo, dalle condizioni al contorno, che
e, pertanto, otteniamo:
Quindi, attraverso le condizioni al contorno si è ricavato che:
Ora, per
sappiamo, dalle condizioni al contorno, che
Quindi, sapendo dalla goniometria che il
Nel nostro caso, allora, possiamo imporre che:
Quindi si è ricavato:
e
si annulla per multipli interi di :
otteniamo:
Sostituendo tale valore di
nell’autovalore energia
si ottiene:
Si noti che il livello nel quantum well, , è quantizzato in quanto dipende da un numero intero
Pertanto, si può imporre che i diversi livelli nel well sono:
Se cambiassimo la larghezza del well si ha che:
63
.
A livello fisico si ha che se aumentando la larghezza del well l’elettrone cade dalla banda di conduzione alla
banda di valenza lasciando così una lacuna nel I° livello, emettendo un fotone.
Se la larghezza del well fosse ridotta i livelli si innalzano e quando gli elettroni decadono emettono fotoni ad
una frequenza diversa. Questa ultima casistica è adottata nella realizzazione di laser a frequenze diverse.
Schematicamente:
In forma generale possiamo esprimere
come:
-
Il Quantum Wire (Filo Quantico)
Il filo quantico è una ulteriore riduzione dello strato di
rispetto al quantum well in maniera tale da
ottenere due dimensioni, che nel nostro caso sono e , confrontabili mentre la restante dimensione
rimane molto più grande di esse.
Consideriamo la eterostruttura avente la seguente condizione:
Una struttura avente questa caratteristica prende il nome di Quantum Wire.
Graficamente:
Per studiare un dispositivo di questo tipo ci si serve dell’Equazione di Schrodinger.
Si noti che l’elettrone oltre a risentire dei potenziali periodici dei reticoli dei due materiali risente anche del
potenziale della barriera, pertanto bisognerà aggiungere all’operatore Helmitoniano anche il potenziale della
barriera
.
L’Equazione di Schrodinger in forma contratta è della forma:
Dove, esplicitando l’operatore hamiltoniano diviene:
Si osservi che la struttura è traslazionalmente invariante nella direzione , cioè che effettuando una
traslazione arbitraria lungo y le proprietà chimico-fisiche non cambiano.
Di conseguenza, l’invarianza traslazionale lungo una direzione si traduce, matematicamente, nel separare le
variabili nell’equazione differenziale:
64
Pertanto, sostituendo nell’Equazione di Schrodinger otteniamo:
Ora, considerando le equazioni differenziali rispetto
65
e z ricaviamo:
Si noti che l’equazione differenziale rispetto è proprio l’Equazione di Schrodinger nel caso di un elettrone
libero avente massa effettiva
, difatti risolvendola si ricava l’autovalori energia dell’elettrone stesso lungo
:
Quindi, sapendo che l’autovalore energia nelle tre direzioni
di rispettivamente lungo
, allora si può scrivere:
è dato dalla somma dei singoli contributi
Dove:
Pertanto si può affermare che l’elettrone è libero di muoversi in banda di conduzione come se fosse un
‘elettrone libero’ avente massa effettiva e l’andamento è un moto parabolico e continuo e ad ogni valore di
corrisponde un valore di . A causa di ciò il quantum wire viene definito a dimensionalità 1D.
Ora consideriamo la componente lungo
Graficamente:
66
E’ evidente che la probabilità di trovare l’elettrone nella barriera è nulla in quanto essa è infinita.
Al di fuori del wire, sia in che in ,
, e quindi l'unica soluzione possibile è
e
, che a
sua volta implica che tutti i valori di energia
e
sono consentiti.
All'interno della buca di potenziale bidimensionale di ampiezza e , l'equazione di Schrodinger si
semplifica in:
Il che significa che la soluzione di
e
è:
Mentre l’autovalore energia è:
Verificando le condizioni al contorno per la buca quantica infinita ricaviamo che:
Pertanto studiando l’autofunzione ricavata dall’Equazione di Schrodinger nella buca quantica infinita
possiamo esplicitare il valore di
e :
Per
e
otteniamo:
sappiamo, dalle condizioni al contorno, che
e
e, pertanto,
Quindi, attraverso le condizioni al contorno si è ricavato che:
Ora, per
e
e
sappiamo, dalle condizioni al contorno, che
otteniamo:
e
mentre
67
Quindi, sapendo dalla goniometria che il
si annulla per multipli interi di :
Nel nostro caso, allora, possiamo imporre che:
Quindi si è ricavato:
Sostituendo tale valore di
e
nell’autovalore energia
e
si ottiene:
Si noti che i livell nel quantum wire,
e , sono quantizzati in quanto essi dipendono dal un numero intero
e
.
Quindi è come se fosse una griglia di livelli quantizzati di energia lungo e z e il livello su cui si trova
l’elettrone è dato dalla combinazione di
e .
Dove è evidente che il livello fondamentale (cioè il più basso livello energetico) è dato dalla combinazione
e
.
Per la determinazione del secondo livello energetico si procede ricavando prima il livello energetico lungo
con
avente
e poi il livello energetico lungo con
avente
. Dopo si ripete il
procedimento al contrario, con
avente
e poi il livello energetico lungo con
avente
ottenendo, così, i livelli
e
.
Il livello energetico più altro tra
e
rappresenta il secondo livello energetico.
Tale procedura si ripete per la determinazione dei restanti livelli.
68
-
Il Quantum Dot (Punto Quantico)
Il punto quantico è una ulteriore riduzione dello strato di
rispetto al quantum wire in maniera tale da
ottenere tre dimensioni, che nel nostro caso sono
e , confrontabili.
Consideriamo la eterostruttura avente la seguente condizione:
Una struttura avente questa caratteristica prende il nome di Quantum Dot, dove si assumerà che esso sia
immerso in un potenziale infinito
.
Graficamente:
Si noti che l’elettrone oltre a risentire dei potenziali periodici dei reticoli dei due materiali risente anche del
potenziale della barriera, pertanto bisognerà aggiungere all’operatore Helmitoniano anche il potenziale della
barriera
.
L’Equazione di Schrodinger in forma contratta è della forma:
Dove, esplicitando l’operatore hamiltoniano diviene:
Di conseguenza, si traduce, matematicamente, nel separare le variabili nell’equazione differenziale:
Pertanto, sostituendo nell’Equazione di Schrodinger otteniamo:
Ora, considerando le equazioni differenziali rispetto
e z ricaviamo:
69
70
Si noti che non c’è alcuna Equazione di Schrodinger nel caso di un elettrone libero e, pertanto, a causa di ciò
si può affermare che l’elettrone non sarà libero in nessuna direzione
divenendo, così, il quantum dot
una struttura a dimensionalità 0D.
E’ evidente che la probabilità di trovare l’elettrone nella barriera è nulla in quanto essa è infinita.
Al di fuori del dot, sia in
,
, e quindi l'unica soluzione possibile è
e
, che a sua volta implica che tutti i valori di energia
e
sono consentiti.
All'interno della buca di potenziale tridimensionale di ampiezza
e , l'equazione di Schrodinger si
semplifica in:
Il che significa che la soluzione di
e
è:
Verificando le condizioni al contorno ricaviamo che:
Pertanto studiando l’autofunzione ricavata dall’Equazione di Schrodinger in corrispondenza delle barriere di
potenziale infinito possiamo esplicitare i valori di ,
e :
Sostituendo tale valore di
,
e
nell’autovalore energia
,
si ottiene:
In conclusione, possiamo affermare che il quantum dot è la struttura quantica base per realizzare i transistor a
singolo elettrone (SET) mentre il quantum well è la struttura quantica base per la realizzazione di modulatori
ottici (tipo Mach-Zehnder) e i laser.
71
72
Appunti di DISPOSITIVI ELETTRONICI PER I
SISTEMI INFORMATIVI
Per il Corso di Laurea in Ingegneria dell’Informazione
- PARTE 5 –
- TRANSISTOR A SINGOLO ELETTRONE (SET) -
-
Il Box a singolo elettrone
I dispositivi a singolo elettrone (SET – Single Electron Transistor) sono dispositivi realizzati in scala atomica
nei quali può essere controllato finanche lo spostamento anche del singolo elettrone.
L’implementazione di tali dispositivi nei circuiti integrati porta all’abbattimento dei consumi di potenza e
l’incremento delle prestazioni dei circuiti, poiché le dimensioni dei dispositivi diminuiscono radicalmente.
I dispositivi a singolo elettrone sono realizzati mediante struttura a quantum dot. Esempio più classico è dato
dal Box a singolo elettrone, costituito da un quantum dot connesso a due elettrodi come rappresenta la figura
in basso, rispettivamente, il modello fisico e il modello circuitale equivalente:
Un elettrodo è collegato al quantum dot attraverso una giunzione tunnel. L’altro elettrodo, chiamato elettrodo
di gate, è accoppiato al quantum dot per mezzo di un isolante attraverso il quale un elettrone non può passare
per effetto tunnel.
Il funzionamento del box a singolo elettrone si basa sul fenomeno del Coulomb Blockade (Blocco di
Coulomb) il quale consiste nel bloccare l’iniezione/eiezione di un singolo elettrone dal o verso il quantum
dot. Il bloccaggio coulombiano è un fenomeno associato alla quantizzazione della carica in un sistema in cui
il movimento degli elettroni è vincolato all’effetto tunnel.
Si consideri il diagramma a bande mostrato in basso:
73
74
Lo stato energetico
è occupato. Pur applicando una tensione , il livello
disponibile è superiore a
quello dell’elettrone,
, che quindi non può passare sul box per effetto tunnel.
L’energia di carica
rappresenta la differenza di energia tra lo stato energetico
e lo stato
.
Se la tensione applicata al sistema è tale da portare il livello energetico
ad allinearsi con il livello di
Fermi nella regione di sinistra (riferita all’elettrodo),
, allora l’elettrone potrà passare sul dot per effetto
tunnel ovvero se l’energia
fornita al sistema è maggiore o uguale a
.
In caso contrario, il passaggio di un ulteriore elettrone sul dot è impedito.
Graficamente:
Il bloccaggio coulombiano avviene fra lo stato generico in cui ci sono elettroni e quello in cui ce ne sono
.
E’ possibile tracciare una caratteristica in relazione al numero di elettroni nel dot, , e alla tensione
osservando, così, la discretizzazione della carica:
Se si applica una tensione al gate, un elettrone dell’elettrodo può guadagnare sufficiente energia per
passare nel dot per effetto tunnel, caricandolo negativamente. Un ulteriore incremento della tensione di gate
può portare il numero di elettroni a due. Quindi, in un box a singolo elettrone, il numero di elettroni nel
quantum dot è controllato, uno per volta, per mezzo della tensione di gate .
Quando la dimensione del quantum dot è piccola, l’energia di carica
di una singola carica in eccesso nel
dot aumenta. Se la dimensione del quantum dot è sufficientemente piccola e
è molto più grande
dell’energia termica
, non ci sono elettroni che si muovono per effetto tunnel né da né verso il box.
Il numero di elettroni nel dot assume un valore costante praticamente pari a zero, quando entrambi gli
elettrodi sono a terra. L’energia posseduta dagli elettroni dipende anche dalla temperatura del sistema.
Se l’energia termica
è maggiore di
il singolo elettrone può comunque fluire attraverso la giunzione
tunnel autonomamente per fluttuazioni termiche.
La condizione, quindi, per bloccare il passaggio di elettroni per attivazione termica è che:
Dove è la capacità del sistema quantum dot, è la carica dell’elettrone, è la temperatura del sistema
espressa in Kelvin ed, infine,
è la costante di Boltzmann.
Ciò implica che la temperatura sia solitamente inferiore ad
per dimensioni di
.
Per osservare il fenomeno di tunneling o l’effetto di Coulomb Blockade del singolo elettrone è necessario
che si verifichi un’ulteriore condizione: l’effetto tunnel deve essere tale da non consentire la delocalizzazione
dell’elettrone sulle facce del condensatore, perché la trattazione, in tal caso, risulterebbe erronea.
L’altra condizione è che la resistenza di tunneling
della giunzione deve essere maggiore della resistenza
quantistica .
Questa condizione è richiesta per sopprimere le fluttuazioni quantistiche nel numero di elettroni del dot in
modo che essere siano sufficientemente piccole; ciò consentirà alla carica di essere ben localizzata sul
quantum dot. La condizione è ottenuta assumendo il principio di indeterminazione di Heisenberg:
Assumendo
come energia di carica del quantum dot e
forma di una costante di tempo
.
Dal principio di indeterminazione si ha:
come tempo di permanenza sul dot, nella
Da cui si ottiene:
Con:
-
Analisi elettrica del box a singolo elettrone
Prendiamo in considerazione lo schema circuitale del box a singolo elettrone:
Applicando le LKT alla maglia interna otteniamo:
75
Da cui la tensione applicata al gate è data dalla somma:
Dove, sapendo che la tensione ai capi di una capacità è data dal rapporto della carica contenuta nel
condensatore per la capacità stessa del condensatore:
Sostituendo in
otteniamo:
Attraverso la Legge conservazione della carica abbiamo che la carica presente nel quantum dot è:
Ovvero:
Mentre la capacità totale del sistema quantum dot è:
Pertanto si sono ricavate le tre relazioni fondamentali del box a singolo elettrone:
1.
2.
3.
Si suppone, ora, che un elettrone attraverso la giunzione tunnel per effetto tunnel giungendo al quantum dot
in maniera tale che presenti una variazione di carica da –
a–
.
Definiamo:
Dove:
rappresenta l’energia spesa dal sistema per portare un elettrone
nel dot;
rappresenta l’energia necessaria per portare elettroni nel dot;
: rappresenta il lavoro speso da per portare
elettroni nel dot a
partire da elettroni iniziali.
76
Quindi l’intervallo di Coulomb Blockade è definito:
77
Pertanto quando si è nell’intervallo di Coulomb Blockade il numero di elettroni nel dot rimane fisso.
Definiamo, ora, l’energia libera del sistema per una transizione da –
a–
elettroni:
Dove la variazione di energia di carica per una transizione da –
a–
elettroni nel dot è pari a :
Con:
Pertanto si ottiene:
Infine, il lavoro
speso da
per una transizione da –
a–
elettroni nel dot è dato da:
Dove, sappiamo che:
Pertanto il lavoro
è espresso come:
Ricaviamo, ora, la variazione di carica
per una transizione da –
a–
e servendoci delle tre equazioni fondamentali del box a singolo elettrone.
Prendiamo in considerazione la tensione applicata al gate:
elettroni partendo da
Dalla Legge di conservazione di carica abbiamo ricavato che:
Quindi esplicitando
e sostituendola in
Sapendo infine che la somma
Ora esplicitiamo
78
otteniamo:
è uguale alla capacità complessiva del quantum dot, si ha:
:
Pertanto si è ricavata la carica
Ora, per una transizione da –
in funzione di
e .
a–
elettroni nel dot si ha una variazione di carica
Dove:
Pertanto si ricava:
Quindi, ritornando al lavoro
si ottiene:
In conclusione, l’energia libera del sistema
Adesso poniamo la condizione:
è pari a:
:
Quindi:
Pertanto isolando
79
:
In conclusione possiamo affermare che:
Definiamo, ora, l’energia libera del sistema per una transizione da –
Dove la variazione di energia di carica per una transizione da –
a–
a–
elettroni:
elettroni nel dot è pari a :
Con:
Pertanto si ottiene:
Infine, il lavoro
speso da
per una transizione da –
Dove, sappiamo che:
Pertanto il lavoro
è espresso come:
a–
elettroni nel dot è dato da:
Ricaviamo, ora, la variazione di carica
per una transizione da –
a–
e servendoci delle tre equazioni fondamentali del box a singolo elettrone.
Prendiamo in considerazione la tensione applicata al gate:
elettroni partendo da
Dalla Legge di conservazione di carica abbiamo ricavato che:
Quindi esplicitando
e sostituendola in
Sapendo infine che la somma
Ora esplicitiamo
otteniamo:
è uguale alla capacità complessiva del quantum dot, si ha:
:
Pertanto si è ricavata la carica
Ora, per una transizione da –
in funzione di
e .
a–
elettroni nel dot si ha una variazione di carica
Dove:
Pertanto si ricava:
Quindi, ritornando al lavoro
si ottiene:
In conclusione, l’energia libera del sistema
è pari a:
:
80
Adesso poniamo la condizione:
Quindi:
Pertanto isolando
:
In conclusione possiamo affermare che:
Unendo i due semi-intervalli ricavati si ottiene il range di valori di affinché il numero di elettroni nel dot
rimane invariato, cioè che si è in condizione di Coulomb Blockade:
Dove, per
diviene:
E così via per valori multipli interi di …
-
Transistor a Singolo Elettrone (SET)
Sebbene la struttura a box a singolo elettrone possa controllare il numero di elettroni in un quantum dot, esso
non ha proprietà di commutazione.
I dispositivi di commutazione sono elementi essenziali nei circuiti logici quindi per soddisfare questa
esigenza nei circuiti ULSI si considerano i transistor a singolo elettrone (SET).
Essi sono dispositivi a tre terminali che possono trasferire elettrone dal source al drain, uno alla volta. Quello
che cambia rispetto al box è che il quantum dot è separato da due elettrodi (source e drain) mediante due
giunzioni tunnel ed è accoppiata capacitivamente ad un elettrodo di gate.
Schematicamente:
81
Mentre il modello elettrico del SET è il seguente:
82
Il principio di funzionamento del SET si basa, sostanzialmente, sul box a singolo elettrone con l’aggiunta di
un secondo elettrodo di drain:
Attraverso il Teorema di Thevenin studiamo i due box ricavando le tensione equivalenti alle porte
e le loro capacità equivalenti:
-
I° BOX: porta
e
La capacità equivalente vista alla porta
è pari a:
Mentre, per la Legge di conservazione di carica si ha che:
Dove sappiamo che:
Pertanto sostituendo nella conservazione di carica otteniamo:
Dove si ricava:
In conclusione, per il I° BOX si è ricavato:
-
II° BOX: porta
La capacità equivalente vista alla porta
è pari a:
Mentre, per la Legge di conservazione di carica si ha che:
Dove sappiamo che:
83
Pertanto sostituendo nella conservazione di carica otteniamo:
Dove si ricava:
In conclusione, per il II° BOX si è ricavato:
Sapendo dal Box a singolo elettrone che l’intervallo di valori di
pari a:
affinché si realizzi il Coulomb Blockade è
Applicando un’analogia ai due box che costituiscono il SET si ricava:
Ricaviamo, ora, per quale range di valori di
e il SET è in regione di Coulomb Blockade a partire dai
due intervalli, riferiti rispettivamente per il I° e II° Box, riportati sopra.
Dall’analisi elettrica trattata in precedenza attraverso il Teorema di Thevenin si è ricavato che:
Pertanto sostituendo nei due intervalli di Coulomb Blockade, essi diventano:
84
Prendiamo in riferimento l’intervallo di Coulomb Blockade per il I° Box è ‘spezziamolo’ in due semiintervalli:
1.
2.
Risolvendo il primo semi-intervallo mettendo in evidenza
si ricava che:
1.
Mentre per il secondo semi-intervallo si ottiene:
Quindi, il range di valori di
affinché si verifichi il Coulomb Blockade è:
Prendiamo in riferimento l’intervallo di Coulomb Blockade per il II° Box è ‘spezziamolo’ in due semiintervalli:
3.
4.
Risolvendo il primo semi-intervallo mettendo in evidenza
si ricava che:
2.
Mentre per il secondo semi-intervallo si ottiene:
Quindi, il range di valori di
Ma sapendo che:
Diviene:
affinché si verifichi il Coulomb Blockade è:
85
In conclusione, le relazioni fondamentali che descrivono il range di valori di
Coulomb Blockade sono:
e
in cui si verifica il
86
E’ possibile tracciare la caratteristica
semplicemente effettuando l’analogia con l’equazione della
retta, del tipo
, dove si effettua l’associazione delle variabili
e
.
Procedendo per valori di
otteniamo:
Quindi, lungo l’asse delle ascisse il Coulomb Blockade si verificherà per valori di
Invece, per valori di
e per
.
ci serviamo dell’analogia:
Di cui, ‘spezzando’ in due semi-intervalli ricaviamo:
1.
2.
Attraverso l’associazione delle variabili,
del tipo:
1.
2.
Che risolte divengono:
1.
2.
e
, esse sono riconducibili a due equazioni delle rette
Quindi graficamente si traduce in una caratteristica di tipo romboidale dove vengono delimitate tutte le
regioni di Coulomb Blockade per valori di in funzione di e . L’area sottesa del rombo indica la
regione di Coulomb Blockade mentre i ‘picchi’ evanescenti evidenziati in azzurro rappresentano il passaggio
di corrente
in funzione di
(seppur discretizzata a causa del passaggio del singolo elettrone) per valori
di e
al di fuori delle regioni di Coulomb Blockade.
Mentre la caratteristica
, essa è della forma:
87
-
I Rates Tunneling
88
Si vuole, ora, individuare una procedura fisica per calcolare la corrente nel SET.
Enunciamo il Rate di tunneling:
Dove:
indica la variazione di energia libera del sistema nella transizione da
elettroni;
elettroni a
indica l’energia termica del sistema;
indica la carica dell’elettrone;
Resistenza di tunneling.
Si esplicita, inoltre, il Rate totale dell’effetto tunneling come:
Dove:
Rate di tunneling di source;
Rate di tunneling di drain.
Ed infine la probabilità di trovare
elettroni nel dot è pari a:
Si ricava:
RATE EQUATION: essa è una equazione di bilancio nel tempo data dalla differenza tra un processo di
generazione di elettroni e un processo di perdita di elettroni.
Si noti che la rate equation si presenta come una equazione differenziale del primo ordine nel tempo dove il
termine
rappresenta la velocità di variazione della probabilità di trovare elettroni nel dot.
I primi due termini dell'equazione principale, sopra, danno il rate di variazione della probabilità dagli stati
e
agli stati adiacenti , mentre gli ultimi due termini danno il rate di variazione della probabilità
dagli stati agli stati adiacenti
e
.
Sapendo, inoltre, che:
Pertanto la corrente
è pari a:
Pertanto la corrente
è proporzionale alla carica dell’elettrone per la differenza tra la velocità con cui un
elettrone entra ed esce dal dot (dal source verso il drain).
-
Applicazioni dei SET nei circuiti logici
Per implementare l’applicazione dei SET nei circuiti logici ci sono due logiche di implementazione:
1. Associare al singolo elettrone il livello logico alto (1);
2. Utilizzare il dispositivo nella logica di interruttore trascurando il numero di elettroni nel dot: quando
c’è il passaggio di elettroni nel dot si associa il livello logico alto (1) mentre in condizione di
Coulomb Blockade si associa il livello logico basso (0).
Nella 1. logica di implementazione vi è il rischio che ci possano essere errori di ‘interpretazione’ logica
indotti da fluttuazioni elettriche mentre nella 2. logica il sistema risulta essere più stabile.
Affinché il SET possa essere implementato nei circuiti logici si ricavano dei modelli analitici del SET sulla
base delle seguenti condizioni:
-
I terminali di source e drain sono connessi a delle capacità (elettrolitiche) molto più grandi rispetto
alle capacità intrinseche del SET. Questo assicura che le caratteristiche del SET non vengano
disturbate da correnti indotte dalla circuiteria esterna al SET, dove solo il contributo in tensione
(sempre della circuiteria esterna) può interagire col SET stesso.
-
Le resistenze di tunneling,
-
Per una data tensione di gate
-
Il SET deve lavorare in condizione di stazionarietà:
e
, devono essere necessariamente uguali tra loro.
si considerano solo i più probabili numeri di elettroni coinvolti.
Dove:
Si noti che la corrente
assume valore massimo quando la tensione
è nulla:
89
Mentre la tensione
Dove
è pari a:
risulta essere una funzione periodica di periodo pari a
90
.
Pertanto fissato un valore a
si hanno tutti i termini costanti a meno di .
Graficamente la corrente si presenta come:
-
Rete di Pull-Up & Pull-Down in tecnologia SET
Una porta CMOS statica complementare è costituita da due reti di transistor: il pull-up (PUN = Pull-Up
Network) realizzato con pMOS; il pull-down (PDN = Pull-Down Network) realizzato con nMOS. Il nodo di
uscita si trova tra PUN e PDN, come indicato dallo schema in basso:
A seconda della configurazione degli ingressi
il nodo di uscita (OUT) può essere connesso
o a massa o a
. Affinché la porta logica funzioni correttamente, il nodo di uscita non deve mai essere
connesso allo stesso tempo sia a massa sia a
e neppure che l’uscita sia in alta impedenza (isolata dalla
massa e da
). Ciò significa che per ogni configurazione degli ingressi uno e uno solo tra PUN e PDN
devono essere accesi. Infatti, se il PUN e il PDN sono entrambi spenti il nodo di uscita risulterebbe isolato
(condizione di alta impedenza) e la sua tensione sarebbe indeterminata. Se, al contrario, sia il PUN sia il
PDN fossero accesi, il nodo di uscita assumerebbe un potenziale intermedio tra 0V e
dando luogo ad un
valore logico indeterminato.
La più semplice porta logica che si può realizzare è l’INVERTER, ovvero la funzione logica NOT. L’inverter
CMOS statico è il mattone fondamentale di qualsiasi circuito logico CMOS. La funzionalità e il
comportamento elettrico di porte logiche più complesse possono essere derivate come facile estensione del
comportamento dell’inverter.
Lo schema circuitale di un inverter CMOS statico è riportato in basso:
Il PDN è costituito da un nMOS mentre il PUN è costituito da un pMOS. In prima approssimazione ciascun
transistor può essere schematizzato come un interruttore: quando
l’interruttore è chiuso (cioè
l’nMOS è in conduzione lasciando che la corrente scorra verso portandola a mentre il pMOS è
interdetto) mentre per
l’interruttore è aperto (cioè l’nMOS è interdetto mentre il pMOS è in
conduzione lasciando sì che l’uscita
si scarichi a zero – supposto che essa sia inizialmente carica a ).
Ora si traccia lo schema elettrico equivalente della rete pull-up & pull-down in tecnologia SET considerando
(dalle condizioni dettare prima per l’implementazione in circuiti logici) il sistema in condizione di
stazionarietà:
.
Determiniamo, ora, per quali valori di
capacitivo.
il SET permette la carica (pull-up) e scarica (pull-down) del carico
91
Iniziamo a studiare la rete di Pull-Up:
Si ricavano le LKT alle due maglie esterne:
Pertanto, dalle LKT, esplicitando la tensione ai capi del carico capacitivo otteniamo:
Dove con l’apice alla tensione si indica il valore per la quale si è fuori dalla regione di Coulomb Blockade
affinché possa scorrere corrente e, quindi, caricare il carico capacitivo .
Quindi affinché la tensione di uscita sia pari alla tensione di alimentazione
(cioè che il condensatore
si carichi fino ad una tensione pari a
) è indispensabile che la tensione
sia nulla (osservando la
LKT(2)):
Quindi, attraverso la LKT(1) ricaviamo che:
Dove la tensione
è pari a:
Quindi sostituendo nella LKT(1) otteniamo che si è fuori dalla regione di Coulomb Blockade e, quindi, il
carico capacitivo può caricarsi fino a
per valori di
pari a:
92
Studiamo, in conclusione, la rete di Pull-Down:
Si ricavano le LKT alle due maglie esterne:
Pertanto, dalle LKT, esplicitando la tensione ai capi del carico capacitivo otteniamo:
Dove con l’apice alla tensione si indica il valore per la quale si è fuori dalla regione di Coulomb Blockade
affinché possa scorrere corrente e, quindi, scaricare il carico capacitivo .
Quindi affinché la tensione di uscita sia pari a zero (cioè che il condensatore si scarichi fino ad una
tensione pari a ) è indispensabile che la tensione
sia nulla (osservando la LKT(2)):
Quindi, attraverso la LKT(1) ricaviamo che:
Dove la tensione
è pari a:
Quindi sostituendo nella LKT(1) otteniamo che si è fuori dalla regione di Coulomb Blockade e, quindi, il
carico capacitivo può scaricarsi fino a 0V per valori di
pari a:
93
-
Vantaggi e svantaggi dei SET rispetto ai MOSFET
Il vantaggio principe dei transistor a singolo elettrone rispetto ai comuni MOSFET, come detto prima, è
rappresentato dal basso consumo di potenza; gli aspetti negativi sono però rappresentati dai seguenti
problemi:
- Funzionamento a basse temperature;
- Elevata impedenza di uscita.
Attualmente, per poter funzionare a temperatura ambiente, il dispositivo SET deve avere dimensioni inferiori
ai 10nm. Strutture di tali dimensioni sono difficili da realizzare con la tecnologia attuale. Inoltre, l’elevata
impedenza di uscita (maggiore di 26kΩ) è giustificata dall’elevata resistenza delle giunzioni tunnel.
E' interessante notare che le grandezze che controllano il dispositivo e che ne permettono la misura sono
macroscopiche: la tensione di gate, ad esempio, è tipicamente dell'ordine dei mV; la corrente che scorre nel
dispositivo è piccola ma misurabile (dai pA ai nA), e questo nonostante il fatto che il trasporto sia
rigorosamente affidato al passaggio sequenziale di un elettrone alla volta.
94
95
Appunti di DISPOSITIVI ELETTRONICI PER I
SISTEMI INFORMATIVI
Per il Corso di Laurea in Ingegneria dell’Informazione
- PARTE 6 –
- FOTONICA -
L’INTEL ha iniziato lo studio sulla fotonica dopo un’analisi della Legge di Moore e, soprattutto, cercando di
risolvere i problemi di surriscaldamento delle piste metalliche costituendo un circuito integrato.
Nella tecnologia attuale, i chip presentano i collegamenti interni distribuiti su 6 strati di silicio e questo può
comportare l’insorgere di effetti capacitivi a causa della presenza di un dielettrico nel mezzo.
Ci possono essere, perciò, nelle commutazioni dei bit dei ritardi di propagazione che, considerati in un
intervallo di tempo considerevole, possono degradare l’informare rendendola inutilizzabile.
Tutti questi fattori hanno spinto la INTEL ad investire nelle interconnessioni ottiche.
Guardando il grafico in basso di noti la resa di diverse tipologie di materiale utilizzati per soddisfare delle
precise regole di progetto:
Si noti che fissata una regola di progetto è possibile abbassare
solo cambiando il materiale oppure
riducendo la costante dielettrica
. In effetti, si veda che la curva del rame coincide con la curva
dell’alluminio a basso (con costante dielettrica).
Dal grafico si evince che la curva con la miglior resa è quella del rame + aria che consiste in interconnessioni
‘a ponte’ ma, a causa della propria costituzione fisica, risulta poco robusto agli shock e, pertanto, non verrà
mai utilizzato.
Data la difficoltà nel realizzare interconnessioni veloci, miniaturizzate e a basso calore disperso la INTEL ha
ovviato il problema realizzando un chip costituito in questo modo:
elettronica
ottica
ottica
elettronica
Il chip è costituito da una sezione elettronica, una interfaccia ottica con connessa una portante ottica.
A valle del chip vi è la sezione elettronica che elabora il segnale di natura elettrica e lo trasmette
all’interfaccia ottica che, sotto opportune operazioni, converte il segnale elettrico in segnale ottico.
Attraverso la portante ottica il segnale viene inviato alla interfaccia ottica che si trova a monte del chip, ove
provvederà a convertire il segnale da ottico ad elettrico.
96
Dopo questa fase, il segnale convertito può essere inviato alla restante parte elettronica che provvederà ad
elaborare secondo progetto.
Pertanto, nella sezione ottica è importante individuare quali dispositivi li costituisce:
1.
2.
3.
4.
5.
Sorgente di luce;
Modulatori ottici;
Guide d’onda;
Multiplexer ottici;
Filtri ottici.
Il problema principale nella realizzazione di tale chip rimane la integrazione del silicio con l’ottica.
Per ovviare a tale problema sono stati adottati due approcci:
1. APPROCCO FRONT-END: consiste nella realizzazione di componenti ottici allo stesso livello dei
circuiti integrati. Per fare ciò il materiale adottato è principalmente il silicio ove viene denominata
come tecnologia SOI (Silicon On Insulator – Silicio su Isolante).
2. APPROCCIO ABOVE IC: consiste nella realizzazione di componenti ottici ‘sopra’ i circuiti
integrati. Pertanto vi sono due possibilità:
a. Realizzare i circuiti ottici con gli elettronici che possono essere depositati sopra i circuiti
integrati: come i silicati drogati del tipo nitruro di silicio, ossido di silicio ecc.
b. Separare la fabbricazione dei circuiti ottici da quelli elettronici formando il wafer bouding tra i
due chip.
La scelta, da parte di INTEL, si è diretta verso il 1° approccio in quanto il 2° approccio, attraverso il wafer
bouding, risulta estremamente costoso.
Vediamo, ora, come è costituita una guida d’onda ottica basata sulla tecnologia SOI:
Il
presenta un indici di rifrazione pari a:
, mentre il silicio puro presenta un indice di
rifrazione pari a:
.
Si deve capire, ora, la zona in cui il silicio è trasparente in modo da poter propagare il fascio laser.
L’indice di rifrazione del silicio nell’intervallo di lunghezze d’onda vale:
Fissando a seconda dei parametri geometrici
e è possibile avere il modo fondamentale quasi TE
(Trasverso Elettrico) o modi fondamentali di altro ordine. Il tutto ha dipendenza dai lobi e, pertanto, fissando
un opportuno valore di è possibile avere entrambi i modi fondamentali TE e TM.
97
98
La guida, in questo caso, si dice MODO MODALE in quanto coesistono i modi fondamentali TE e TM.
La configurazione di campo quasi TM è data da:
Dove:
Con:
.
Pertanto, si ottengono:
Si prova che quando la struttura tende ad essere di tipo ‘rettangolare’ risulta essere;
Mentre, quando la struttura assume una configurazione più ‘quadrata’ risulta:
L’indice efficiente maggiore indica, quindi, il modo fondamentale maggiore.
-
Guide d’onda ottiche
Vi è una tecnologia relativamente nuova per la trasmissione della luce la quale usa dei ‘condotti’ dielettrici,
che prendono il nome di guide d’onda ottiche.
Una guida d’onda ottica permette di dirigere un fascio luminoso anche in luoghi difficili ed, inoltre, permette
la realizzazione di dispositivi miniaturizzati per l’ottica e la optoelettronica.
Un mezzo avente indice di rifrazione maggiore
viene inserito nel mezzo di un mezzo avente indice
di rifrazione inferiore
agendo come 'trappola' per luce, entro la quale i raggi ottici rimangono
confinati a causa di molteplici riflessioni totali interne al confine stesso. Poiché questo effetto facilita il
confinamento della luce generata all'interno di un mezzo avente indice di rifrazione, può essere sfruttato nel
trasportare la luce da una posizione all'altra.
Le geometrie utili per le guide d'onda sono illustrate nelle due figure in basso.
La guida d'onda possono essere fabbricate in diverse configurazioni: le curve S sono utilizzate per
compensare l'asse di propagazione, il ramo Y gioca il ruolo di un divisore di fascio o combinatore mentre
due rami Y possono essere usati per realizzare un interferometro Mach-Zehnder.
Due guide d'onda in intersezione possono scambiare potenza e possono essere utilizzate come accoppiatori
direzionali.
Le guide d'onda sono realizzati mediante strati di GaAs e AlGaAs con indice di rifrazione diversi tra loro.
Prendiamo in riferimento l’accoppiatore ottico direzionale che è schematizzato in basso:
99
Da come si nota, la struttura è composta da due “piste” o, in gergo, guide d’onda separate tra esse da un gap
e aventi nella zona centrale una lunghezza ben definita .
A loro volta, le guide d’onda presentano degli indici di rifrazione tali da permettere al singolo modo di
poter essere riflesso lungo la guida stessa.
Nella trattazione analitica dell’accoppiatore ottico direzionale ci si serve degli indici effettivi
che
possono essere di due tipi, rispettivamente in funzione del modo utilizzato:
Pertanto, il principio di funzionamento dell’accoppiatore ottico direzionale si basa sulla Teoria dei Modi
Accoppiati.
Supponiamo di avere due guide d’onda parallele tra esse, separate da un gap e aventi entrambe lo stesso
indice di rifrazione, come mostrato in basso:
Ora si supponga di voler inviare all’ingresso della guida 1 il singolo modo. Da come si può notare la
propagazione del modo è di tipo evanescente lungo la guida e con l’avanzare della propagazione esso
presenta delle evoluzioni che sono suddivise in step (in questa trattazione):
1. Il singolo modo entra nella guida d’onda 1 con una determinata ampiezza, che è pari a (per
semplicità di trattazione)
2. Il modo, man mano che si propaga lungo la guida 1, ‘sente’ la presenza della guida d’onda 2, avente
anch’essa lo stesso indice effettivo;
3. Per opera dell’Effetto Modale o Tunneling Ottico, il modo oltrepassa il gap fino a giungere alla
guida 2 presentando, però, un’ampiezza minore di ;
4. In questa fase, entrambi i modi sono situati rispettivamente nella guida 1 e 2 presentano la stessa
ampiezza che, anche in questo caso, rimane sempre minore di ;
100
5. Il modo situato nella guida 1 subisce un’attenuazione che porta la sua ampiezza ad essere minore
rispetto al valore iniziale mentre il modo situato nella guida 2 aumenta sempre più la sua ampiezza
fino a raggiungere il valore ;
6. Come penultimo step, il modo nella guida 1 è ormai nullo mentre permane il modo nella guida
d’onda 2, con ampiezza pari a .
7. Il singolo modo è, ora, lungo la guida d’onda 2.
Si noti che al variare del valore di è possibile trasferire il modo da una guida all’altra. Ad esempio, se le
guide d’onda della figura sopra avessero avuto lunghezza pari a
si avrebbe avuto la presenza di entrambi
i modi nelle guide 1 e 2 ma con ampiezze dimezzate, a .
Pertanto, volendo distinguere due casi estremi, possiamo dire che:
1. Il modo viene immesso nella guida 1 ed esce dalla guida 1;
2. Il modo viene immesso nella guida 2 ed esce dalla guida 2.
In conclusione, affinché si possa pilotare il percorso che il modo deve percorrere si applicano due elettrodi
sulla lunghezza di accoppiamento sotto l’azione di una tensione esterna . In funzione del materiale con
cui è composto l’accoppiatore si ha la presenza dell’Effetto Elettro-Ottico:
Dove:
costante che tiene conto del materiale e forma strutturale dell’accoppiatore (compresi gli elettrodi);
variazione degli indici effettivi di rifrazione;
tensione applicata agli elettrodi.
Graficamente:
Per meglio comprendere l’accoppiatore ottico direzionale ci serviamo dell’accoppiatore ottico direzionale
curvilineo.
101
-
Accoppiatore Ottico Direzionale Curvilineo: Risonatore ad anello
L’accoppiatore ottico direzionale curvilineo si presenta nella seguente forma:
L’accoppiatore ottico direzionale curvilineo o anche risonatore ad anello è composto da due guide d’onda
che fungono, rispettivamente, da bus di entrata e bus di uscita. In mezzo alle due guide vi è un anello che
viene distanziato dai bus stessi per opera di due gaps,
e
, di uguale dimensione.
Il principio di funzionamento del risonatore ad anello è il seguente: si supponga di mandare lungo la guida
d’onda 1 un fascio di laser . Questo non avrà alcuna interazione con l’anello fino a quando non giunge al
punto di minima distanza,
, tra l’anello e la guida 1; in questo punto preciso si avrà il tunneling ottico
dove una parte di fascio proseguirà la sua propagazione lungo la guida 1,
mentre l’altra parte starà
propagandosi lungo l’anello.
Quando il modo lungo l’anello giunge al punto di minima distanza tra l’anello stesso e la guida 2,
,
allora una parte di fascio proseguirà la sua propagazione lungo la guida 2, , mentre la restante parte
terminerà il suo percorso congiungendosi ad
nel punto di minima distanza
cedendo ulteriore
energia ad stesso, avendo così compiuto un giro completo lungo l’anello.
102
I° CASO:
Si suppone, ora, di far tendere i gaps
e
2 ad infinito in modo da allontanare le due guide d’onda
dall’anello e che, inizialmente, nell’anello ci sia la presenza del fascio laser avente una quantità di energia
ottica pari a
. Inoltre, a causa della curvatura dell’anello e del contributo di scattering e diffrazione (per
conto delle rugosità superficiali) il fascio laser sarà soggetto a perdite di propagazione.
Man mano che il tempo passa l’energia ottica nell’anello,
, diminuisce con la seguente velocità:
Dove si esprime:
Quindi, risolvendo l’equazione differenziale del primo ordine nel tempo otteniamo:
Quindi:
Si noti, pertanto, che l’andamento dell’ampiezza tempo-variante del campo elettrico nell’anello (inteso come
fascio ottico) si presenta come un andamento esponenziale negativo che tende asintonticamente, per
,
a .
103
Graficamente:
104
Mentre il campo elettrico nell’anello è dato dalla relazione:
Dove rappresenta una coordinata curvilinea mentre la funzione
rappresenta la distribuzione
bidimensionale, normalizzata, del tipo
ed infine
è il coefficiente d’ampiezza tempovariante del campo elettrico nell’anello soggetto a perdite di propagazione.
II° CASO:
Supponiamo, ora, di ridurre i gaps
all’anello.
Graficamente:
in modo da far riavvicinare le guide d’onda
A causa di ciò l’ampiezza tempo-variante del campo elettrico presenterà una variazione di data dalla
relazione:
ove rappresenta la velocit di attenuazione nell’anello dell’ampiezza tempo-variante del campo elettrico,
dove:
tempo di vita medio dei fotoni associato alla guida di uscita (ring-bus d’uscita);
tempo di vita medio dei fotoni associato alla guida di ingresso (ring-bus d’ingresso);
fattore di accoppiamento tra il bus di ingresso e l’anello;
contributo che va ad aggiungersi all’energia dell’anello;
termine che tiene conto della differenza tra la pulsazione angolare
della
pulsazione angolare
105
del fascio
e
tipica del risonatore.
Da quanto detto in merito al principio di funzionamento del risonatore ottico, si ha che quando il fascio
viaggiante sull’anello è in prossimità del punto di minima distanza tra l’anello è la guida d’onda 1,
, (al
termine del giro completo) vi è una ‘interferenza’ con che può essere di due tipi: interferenza costruttiva o
interferenza distruttiva.
1. INTERFERENZA COSTRUTTIVA: essa si verifica quando il fascio viaggiante sull’anello, al
termine del giro completo su di esso, è in prossimità del punto di minima distanza tra l’anello e la
guida 1 è in fase con il fascio portandosi così in condizione di RISONANZA;
2. INTERFERENZA DISTRUTTIVA: essa si verifica quando il fascio viaggiante sull’anello, al
termine del giro completo su di esso, è in prossimità del punto di minima distanza tra l’anello e la
guida 1 non è in fase con il fascio e, quindi, non è presente la condizione di risonanza.
Pertanto, quando si è in condizione di risonanza si ha un aumento dell’ampiezza
in quanto il termine
tenderebbe a zero per
.
Procedendo analiticamente, per ottenere interferenza costruttiva si deve porre la condizione:
Dove è un intero.
Poiché la costante di propagazione
è pari a:
Mentre la lunghezza d’onda è data da:
Con la velocità della luce ed
Sostituendo in si ha:
la pulsazione.
Sapendo, inoltre, che:
Dove
è il raggio dell’anello mentre
rappresenta la circonferenza, si ottiene:
In conclusione, sostituendo
con
si ricava la pulsazione di risonanza:
106
E sapendo, infine, che la pulsazione di risonanza è pari a:
Esplicitiamo la frequenza di risonanza dell’anello:
Essendo intero, esso può assumere infiniti valori,
la frequenza di risonanza può assumere infiniti valori:
, allora la pulsazione di risonanza,
,e
NOTA: in fase di progetto, si ha che è un numero intero. Se si volesse, ad esempio, operare ad una
lunghezza d’onda
si procede prendendo il valore intero più vicino a , che in questo caso è 2.
III° CASO:
Supponendo che i gaps 1 e 2 abbiano uguale dimensione,
si vuole determinare il rapporto di
potenza tra il fascio laser e il fascio
e il rapporto di potenza tra e quando si è in condizione di
risonanza in maniera tale da ricavare le caratteristiche del risonatore ad anello.
Essendo i gaps uguali tra loro è possibile esplicitare la relazione che lega i fattori di accoppiamento
e
con i tempi di vita medio e :
Pertanto, nell’ipotesi in cui
sia un fascio continuo si ha che:
Ovvero, si ha la condizione di stazionarietà.
Si ricavi, ora, l’ampiezza
in condizione di stazionarietà:
Ponendo, per semplicità di calcolo:
Otteniamo:
Esplicitando
107
Normalizzando:
Diagrammando il rapporto
Si noti che quando
in funzione della pulsazione
quando si è in risonanza
si ha il picco massimo di energia nell’anello.
Si ricavi, ora, il rapporto di potenza
a partire dal
:
Che in modulo quadro diviene:
Dove esplicitando la potenza del fascio laser nell’anello diviene:
E sapendo, dai calcoli affrontati in precedenza, che:
Quindi, eguagliando le due relazioni di
otteniamo:
, si ottiene:
In conclusione, mettendo a rapporto
con
otteniamo il rapporto di potenza tra il fascio laser
uscente dal bus di uscita e il fascio laser entrante nel bus d’ingresso:
Sapendo inoltre che:
Questi due parametri uguali tra loro solo se i gaps sono anch’essi uguali, quindi:
In conclusione si ricava:
Ricaviamo, infine, il rapporto di potenza
Dove esplicitando
a partire da:
si ha:
Effettuando il modulo quadro dei termini si ricava:
E sapendo che:
Si ha:
Inoltre si è ricavato in precedenza che:
Quindi sostituendo si ricava:
108
Quindi mettendo in evidenza
e raggruppando tutti i termini in
otteniamo:
E sapendo che:
E con:
Otteniamo:
In conclusione mettendo a rapporto la potenza del fascio laser uscente dal bus d’ingresso con la potenza del
fascio laser d’ingresso entrante nel bus d’ingresso si ricava:
Pertanto, ricapitolando i rapporti di potenza sono:
Ora si considerano i rapporti di potenza ricavati in condizione di risonanza e in assenza di perdite lungo
l’anello:
109
I rapporti di potenza divengono:
Quindi, quando si è in condizione di risonanza si ottiene la massima uscita di da
mentre in condizione
di non risonanza si ha la massima uscita di da , come se l’anello non esistesse in questo caso.
In questo preciso caso i gaps devono avere un valore ben preciso, in assenza di perdite, in modo che il fascio
esca dal bus di uscita:
.
Si noti, inoltre, che
cioè il tempo di vita medio del fotone del processo associato è maggiore.
Pertanto:
Dove:
Infine sapendo che:
110
Definiamo:
111
Con:
Il tempo di round-trip è il tempo impiegato da un fascio laser ad entrare nell’anello e compiere il suo
percorso chiuso fino a concludere il giro completo.
Pertanto la relazione che lega
a
è pari a:
Dove, sostituendo
Quindi:
Con:
si ottiene:
E’ possibile realizzare demultiplexer ottici attraverso l’implementazione di più anelli risonatori posti in
cascata tra loro.
Graficamente si ottiene:
Pertanto, dimensionando opportunamente attraverso un’analisi numerica i coefficienti di accoppiamento è
possibile ottenere una risposta pari ad un filtro di
o
, del tipo:
112
113
Appunti di DISPOSITIVI ELETTRONICI PER I
SISTEMI INFORMATIVI
Per il Corso di Laurea in Ingegneria dell’Informazione
- PARTE 7 –
- STRUTTURA LASER A SEMICONDUTTORE -
-
Fisica dei LASER a semiconduttore
Il termine LA(SER) sta per Light Amplification by Stimulated Emission of Radiation’ (amplificazione di luce
mediante emissione stimolata di radiazione) da cui si evince che i Laser a semiconduttore si basano sul
fenomeno dell’emissione stimolata di fotoni, (SER) = Stimulated Emission of Radiation.
Il laser a semiconduttore, pertanto, è basato sul fenomeno della emissione stimolata, che è stata postulata da
Einstein nel 1910.
Nei laser a semiconduttore la radiazione luminosa emessa ha coerenza spaziale e temporale, altamente
monocromatica (avente larghezza di banda molto piccola) e produce fasci di luce altamente direzionali.
Tuttavia, i laser a semiconduttore presentano degli aspetti importanti:
1. Nei laser a semiconduttori le transizioni sono associate alle proprietà di banda dei materiali.
2. Un laser a semiconduttore è molto compatto nelle dimensioni, dell'ordine di
.
3. Le caratteristiche spettrali e spaziali di un laser a semiconduttore sono fortemente influenzate dalle
proprietà del mezzo di giunzione come variazioni dell'indice di rifrazione e bandgap.
I laser a semiconduttore, a causa della loro lunghezza d'onda insieme alla stretta larghezza di riga spettrale,
alta stabilità, alla bassa potenza di ingresso e alla semplicità strutturale hanno un potenziale significativo per
l'applicazione nella tecnologia e nella ricerca di base.
-
Interazioni di fotoni con atomi
Come è noto dalla teoria atomica, un atomo può emettere (creare) o assorbire un fotone subendo delle
transizioni verso il basso o verso l'alto tra i suoi livelli energetici, conservando energia. Le leggi che
governano questi processi sono:
Consideriamo i livelli di energia
e
di un atomo e si è particolarmente interessati nel trattare
l'interazione tra l'atomo ed i fotoni di una modalità di radiazione alla frequenza
, dove
poiché l’energia fotonica
corrisponde alla differenza dei livelli energetici atomici
.
Esistono tre forme di interazione possibili, le quali sono:
a) Emissione spontanea;
b) Assorbimento;
c) Emissione stimolata.
,
a. Emissione spontanea
Si suppone che l'atomo sia inizialmente a livello energetico superiore . Esso può cadere spontaneamente al
livello di energia inferiore
e rilasciare la sua energia sotto forma di un fotone, come mostrato nella figura
in basso.
L’energia del fotone
viene aggiunta all'energia del modo elettromagnetico.
Tale processo prende il nome di 'emissione spontanea' in quanto la transizione è indipendente dal numero
di fotoni che possono essere già presenti nella modalità.
114
b. Assorbimento
Se l'atomo è inizialmente nel livello di energia inferiore
e la modalità di radiazione contiene un fotone, il
fotone può essere assorbito portando così l'atomo al livello di energia superiore , come mostrato nella
figura in basso.
Il processo è chiamato 'assorbimento'.
L'assorbimento è una transizione indotta dal fotone. Essa può verificarsi solo quando la modalità contiene un
fotone.
c. Emissione stimolata
Se l'atomo è a livello energetico superiore
e la modalità contiene un fotone, l'atomo può essere stimolato
ad emettere un fotone nello stesso modo. Il processo è noto come 'emissione stimolata'. Esso è l'inverso
dell’assorbimento.
La presenza di un fotone in una modalità ove siano stati stabili la frequenza, la direzione di propagazione e la
polarizzazione stimola l'emissione di un fotone duplicato ("clone") esattamente con le stesse caratteristiche
del fotone originale, proprio come mostrato nella figura in basso.
Questo processo di ‘amplificazione’ del fotone è il fenomeno che caratterizza e sfruttano i laser a
semiconduttore.
Le tre possibili interazioni tra un atomo e una modalità di radiazione fotonica (emissione spontanea,
assorbimento e di emissione stimolata) dovrebbero essere considerate come le leggi che governano le
interazioni fotone-atomo.
-
Semiconduttori a gap diretto e indiretto
Ci sono anche altre caratteristiche per cui solo alcuni semiconduttori sono adatti per la costruzione di un laser
e questo dipende dalla struttura delle loro bande, infatti oltre alle caratteristiche generali prima definite ne
esistono altre che distinguono i semiconduttori in due categorie: quelli a gap diretto e quelli a gap indiretto, i
primi sono quelli utilizzati nella costruzione dei laser.
Consideriamo solo le transizioni radiative fra banda di valenza e di conduzione, ad ogni decadimento
corrisponde l’emissione di un fotone:
115
Fotoni ed elettroni sono caratterizzati da una certa energia e quantità di moto o vettore d’onda
modulo nel caso dei fotoni è:
, il cui
Dove che rappresenta la pulsazione angolare del fotone e la velocità della luce.
Mentre nel caso degli elettroni il vettore d’onda
varia tra 0 e (Zona di Brillouin) , dove
dalla struttura cristallina del semiconduttore (costante reticolare).
dipende
Nelle transizione fra bande deve valere la conservazione dell’energia e della quantità di moto:
Dove il vettore d’onda
rappresenta la condizione iniziale, cioè quando gli elettroni si trovano inizialmente
in banda di conduzione; mentre, allo stato finale, l’elettrone decade andando in banda di valenza con vettore
d’onda
emettendo un fotone con vettore d’onda pari a .
Difatti, volendo esprimere la conservazione della quantità di moto nel seguente modo:
Il vettore d’onda del fotone,
quindi si ha:
, può essere trascurato poiché le frequenze interessate sono nel visibile, e
Di conseguenza si ottiene:
Una transizione di questo tipo è detta transizione diretta e un semiconduttore in cui ciò avviene è detto a
gap diretto.
Pertanto quando un elettrone decade dalla banda di conduzione alla banda di valenza il suo momento non
deve subire variazione affinché ci sia l’emissione di fotoni: quindi la conservazione della quantità di moto
deve essere rispettata.
Nel caso di semiconduttori a gap indiretto la transizione avviene con l’emissione di un’altra particella : il
fonone (o modo di vibrazione del reticolo).
Tale transizione oltre ad essere meno probabile , può non essere radiativa : l’energia di gap infatti non viene
ceduta totalmente ad un fotone , che contribuisce così all’ intensità del fascio , ma viene ceduta ad altri
portatori come energia cinetica , oppure dissipata in fononi di vibrazione del reticolo, oppure assorbita da
impurità del materiale.
E’ chiaro quindi che gli unici semiconduttori interessanti per la costruzione di un laser o di un led (cioè
idonei all’emissione di fotoni) sono quelli a gap diretto , un esempio è l’ Arseniuro di Gallio ( GaAs) ,
mentre germanio e Silicio sono esempi di semiconduttori a gap indiretto.
116
117
Gap diretto
-
Gap indiretto
Inversione di popolazione
Si parla di inversione di popolazione quando in un sistema costituito da un gruppo di corpi elementari (per
esempio atomi, molecole o elettroni) ci sono più corpi in stato eccitato, ad esempio , che corpi negli stati
di minore energia, ad esempio .
In particolare, l’inversione di popolazione è riferito quando in un semiconduttore ci sia la maggiorazione di
elettroni in banda di conduzione rispetto al numero (o densità) di elettroni siti in banda di valenza.
Questa particolare condizione è la chiave per ottenere l'emissione laser.
-
Struttura Laser a semiconduttore: Cavità risonante di Fabry-Perot
La struttura del laser a semiconduttore può essere realizzata nella seguente maniera:
Una struttura di questo tipo prende il nome di Diodo pin, ove rappresenta il diodo laser per realizzare un
laser a semiconduttore.
La f.e..m. serve a polarizzare direttamente la giunzione pn, quindi a creare l’inversione di popolazione.
In particolare, il materiale di tipo p è costituito da AlGaAs (drogato affinché ci sia maggiorazione di lacune
in banda di conduzione della regione ) mentre la regione centrale (intrinseca) è costituita con materiale a
bandgap diretto quale, ad esempio, GaAs ed, infine, lo strato di materiale di tipo n è sempre costituito da
AlGaAs (drogato affinché ci sia maggiorazione di elettroni in banda di conduzione della regione ).
Per definizione la regione attiva (intrinseca) è il mezzo candidato a emettere fotoni in quanto i materiali
drogati di tipo p ed n hanno un basso indice di rifrazione rispetto alla regione attiva (cioè lo strato di GaAs).
In particolare, se il modo laser si distribuisce all’interno del diodo secondo linee concentriche di campo
elettrico la potenza viene confinata nella regione attiva anche se parte una quota parte di questa potenza si
distribuisce anche al di fuori della regione attiva stessa. In altri termini, si definisce il di confinamento
come il rapporto tra la potenza ottica confinata nella regione intrinseca e la potenza ottica totale:
cioè il fattore di confinamento tiene conto della quota parte della potenza ottica che è confinata nel mezzo
attivo.
A questo punto è opportuno ricordare che il processo fisico candidato per la realizzazione di un laser è
l’emissione stimolata, cioè un fotone che ‘stimola’ il decadimento di un elettrone per ‘emettere’ un altro
fotone coerente con quello incidente (emissione stimolata). Pertanto, affinché sia stimolato il decadimento di
un elettrone a livello energetico inferiore per emettere un fotone è necessario creare l’inversione di
popolazione. Terminato questo processo è indispensabile che ci siano dei fotoni che possano innescare
l’emissione stimolata come un ‘effetto a catena’ dove il primo fotone incidente stimola il decadimento di un
elettrone dalla banda di conduzione affinché possa emettere un fotone coerente a quello incidente; questi due
fotoni, a loro volta, possono stimolare il decadimento di altri elettroni e, quindi, emettere altri fotoni.
Per cui si ha la necessità di far rimanere i fotoni internamente al mezzo attivo in modo tale che il fotone
possa stimolare il decadimento di un elettrone per emettere un altro fotone coerente con quello incidente. A
questo punto si devono manipolare questi due fotoni (incidente e coerente) in modo da farli rimanere
confinati nella regione attiva per stimolare il decadimento di altri elettroni e, quindi, l’emissione di altri
fotoni.
Pertanto, per realizzare un laser serve un terzo elemento (oltre al mezzo attivo e alla f.e.m. per realizzare
l’inversione di popolazione) che è una Cavità Risonante, cioè dove i fotoni devono passare più volte
all’interno del mezzo attivo. In questo modo ad ogni passaggio si stimola il decadimento degli elettroni dalla
banda di conduzione alla banda di valenza emettendo fotoni coerenti con quelli già presenti nel mezzo attivo.
118
La cavità risonante che viene utilizzata in maggior modo è la Cavità di Fabry-Perot:
Supponiamo che la cavità sia lunga L e lungo z il diodo pin può essere visto come una guida d’onda. Agli
estremi della guida sono posti due specchi caratterizzati da un coefficiente di trasmissione
e da un
coefficiente di riflessione , .
Supponiamo, ora, che al primo specchio ci sia un fascio ottico di ampiezza e si vuole valutare l’ampiezza
del campo in uscita alla cavità, .
E’ noto che il campo elettrico che si propaga è in funzione di x, y, z, nella cavità, è della forma:
Dove
è la distribuzione del campo elettrico nel piano , mentre
presenza del campo elettrico nella cavità.
Si definisce la costante di propagazione all’interno della cavità come:
è una costante rappresentante la
Dove:
rappresenta la costante di propagazione ideale della cavità;
parametro intrinseco del materiale in esame;
guadagno modale.
In questa guida (Fabry-Perot) ci possono essere delle perdite di propagazione ed è proprio per questo motivo
che la costante di propagazione è complessa: .
Pertanto essendo una quantità complessa presenterà parte reale:
e parte immaginaria:
Poiché per opera della f.e.m.
vi è lo scorrere di una corrente che inietta i portatori, essi producono un
guadagno che viene tenuto conto dal guadagno modale .
Essendo il diodo pin inteso come una guida d’onda lungo e composto da materiale con perdite (nel caso
reale), il modo laser che si propaga anch’esso lungo presenterà delle perdite perdendo potenza man mano
che si propaga.
Pertanto, per la cavità di Fabry-Perot, si deve considerare un guadagno in quanto man mano che il modo
laser si propaga lungo si hanno alcuni fotoni che vengono persi (no per assorbimento) a causa delle perdite
di propagazione. Quindi si deve considerare il guadagno riferito alla regione attiva (GaAs).
119
Supponendo, ora, di trovarsi in condizione di perdita totale (
la costante di propagazione diviene:
Pertanto il campo elettrico che si propaga nel diodo diviene:
Dove
tiene conto delle perdite all’interno della cavità di Fabry-Perot.
Nei semiconduttori quando si iniettano portatori per opera della corrente generata dalla
(gli
elettroni nella banda di conduzione e lacune nella banda di valenza) essi producono una variazione
dell’indice di rifrazione del materiale proporzionale al numero di portatori iniettati. Tale effetto prende il
nome di EFFETTO PLASMA.
Pertanto, se stiamo iniettando dei portatori di conseguenza cambierà l’indice di rifrazione effettivo dei
materiali p, n e di quello intrinseco rispetto alla condizione di riposo, cioè di non iniezione, con la
conseguente variazione della costante di propagazione .
Quindi il guadagno modale non solo influenza la parte immaginaria della costante di propagazione
(perché compensa la parte di fotoni persi per perdita di propagazione – vista la differenza
) ma
produce anche una variazione dell’indice di rifrazione del materiale rispetto alla condizione di riposo, cioè in
assenza di iniezione. Questa variazione, a sua volta, produce una diminuzione della costante di propagazione
. E’ opportuno sottolineare che l’indice di rifrazione è una proprietà del materiale che spiega come esso
interagisce in presenza di un campo elettrico associato alla luce.
I° CASO: determinare il rapporto tra il campo uscente
e il campo entrante : .
NOTA: Per semplicità di calcolo, trascureremo la quantità
in quanto rimane invariata e, quindi,
durante i calcoli andrà a semplificarsi.
Quando incide sul primo specchio una quota parte viene riflessa all’esterno della cavità,
, e una quota
parte viene trasmessa al suo interno. In particolare si ha che al primo specchio la quantità trasmessa lungo la
cavità,
si propaga lungo L e arriva al secondo specchio.
Di conseguenza al secondo specchio si avrà:
Dove il fascio è caratterizzato da una costante di propagazione lungo la cavità
.
Pertanto, all’incidenza sul secondo specchio, una quota parte sarà trasmessa fuori dalla cavità e una parte
sarà riflessa al’interno della cavità sempre per opera del secondo specchio.
Pertanto al secondo specchio si ha:
Dove:
Pertanto
in totale è pari a:
E sapendo, inoltre, che:
120
Con:
121
diviene:
Quindi:
Mettendo in evidenza
Mettendo a rapporto
si ha:
e
si ricava:
II° CASO: determinare per quale valore di si ha interferenza costruttiva (risonanza) in condizione in
cui
Trascuriamo la parte immaginaria della costante di propagazione e determiniamo per quale valore di si
ha interferenza costruttiva all’uscita della cavità:
Dove è una quantità intera mentre indica la lunghezza della cavità.
Questa condizione, pertanto, ci consente di avere un
finito a fronte di un
Sapendo che:
Con:
e:
Otteniamo:
nullo.
Quindi si ricava:
Isolando
122
otteniamo:
Questa relazione permette di calcolare le frequenze di interferenza costruttiva in trasmissione, cioè in
uscita dalla cavità di Fabry-Perot.
A questo punto, facendo il modulo quadro di si ricava:
Con:
Dire che
significa dire che si deve avere una potenza di uscita
potenza di ingresso nulla
, pertanto si deve imporre che:
Quindi ha senso supporre una potenza
finita a fronte di una potenza
denominatore del rapporto a zero soltanto se a priori supponiamo che:
Con:
Dove si ricava:
Applicando il logaritmo naturale ad ambo i membri:
Pertanto isolando
otteniamo:
a fronte di una
e, quindi, porre il
Dove:
123
Si ottiene:
In conclusione le condizioni necessarie affinché si possa avere un fascio laser è che il guadagno del mezzo
attivo (regione intrinseca) sia maggiore di zero in quanto si deve creare la condizione di inversione di
popolazione. Affinché, inoltre, il diodo pin possa accendersi è necessario far uscire il fascio ottico dalla
cavità imponendo che il guadagno modale sia maggiore di
.
Quando
il laser è in condizione di soglia.
Invece si è in condizione di soglia quando:
In particolare se si pongono le riflettività degli specchi
, sostituendo in
si ha:
Ciò significa che non si hanno perdite pertanto il fascio non uscirà mai dalla cavità di Fabry-Perot.
Pertanto è indispensabile porre una riflettività pari all’unità (in particolare da dove non si vuole che il fascio
laser esca) quindi
mentre la riflettività deve essere parzialmente riflesso in modo tale che il fascio
laser possa in parte uscire dalla cavità e in parte rimanere confinato all’interno della cavità stessa.
Allora, da un punto di vista fisico, le perdite associate agli specchi significa che una volta che all’interno
della cavità si crea un minimo fascio ottico quando il fascio stesso incide il secondo specchio, essendo
parzialmente riflessivo, una parte viene riflessa e una parte trasmessa.
La parte trasmessa rappresenta i fotoni che si sono persi in quanto escono dalla cavità e, quindi, non
partecipano all’emissione stimolata.
Si è visto che il diodo pin funge da sorgente di fotoni (essendo esso un amplificatore ottico per opera della
cavità risonante) in quanto genera esso stesso un fascio ottico che rispetti il II° Principio della
Termodinamica, ovvero che non è possibile creare energia (fotoni) senza spendere lavoro.
Poniamoci, ora, nella condizione di voler eccitare l’emissione stimolata.
Affinché si possa avere emissione stimolata si deve innescare l’inversione di popolazione, cioè aumentare il
numero di elettroni siti in banda di conduzione rispetto al numero di elettroni siti in banda di valenza (in
senso assoluto vuol dire che gli elettroni passano dalla banda di valenza alla banda di conduzione –
condizione no fisica). Pertanto per realizzare l’inversione di popolazione ci si serve di una giunzione
polarizzata direttamente attraverso una
pari a
tale da iniettare gli elettroni dalla banda di
valenza alla banda di conduzione (iniezione di portatori).
Quindi polarizzando direttamente la giunzione
si è fuori dall’equazione termodinamica per cui il sistema
è definito
(cioè quando si è innescata l’inversione di popolazione – invece il sistema è
definito
quando non c’è inversione di popolazione, elettroni in
e lacune in ) ove sono
presenti i
ove sono rappresentati da
(quasi-livello di Fermi per la banda di
conduzione) e
(quasi-livello di Fermi per la banda di valenza) separati, a loro volta, di una quantità
proporzionale a .
Graficamente si mostrano il sistema all’equilibrio per
:
Condizione in cui non c’è l’inversione
di popolazione per opera di
Condizione in cui c’è l’inversione
di popolazione per opera di
Sistema fuori-equilibrio
e il sistema fuori-equilibrio per opera di
Sistema all’equilibrio
Sistema fuori-equilibrio
Nel caso in cui si è creata l’inversione di popolazione, per
, si definisce la Funzione distribuzione
Fermi-Dirac o, semplicemente, Funzione di Fermi per i quasi-livelli di Fermi:
Pertanto la Funzione di Fermi indica la probabilità di trovare un elettrone in un determinato livello
energetico (da non intendersi come una funzione densità di probabilità).
Quindi, la probabilità di trovare gli elettroni in banda di conduzione per
è maggiore rispetto alla
probabilità di trovare gli elettroni per
in banda di conduzione sempre. Analogamente, la probabilità
di trovare le lacune per
in banda di valenza è maggiore rispetto alla probabilità di trovare le lacune
in banda di valenza per
.
124
Dimostrando matematicamente, per
:
Il punto di domanda nella realizzazione del laser è: quanti elettroni si devono iniettare e qual è il valore di
tale che si possa accendere il laser?
Indichiamo con:
ove indica la densità degli elettroni in banda di conduzione e di lacune in banda di valenza; cioè rappresenta
il numero di elettroni e lacune per unità di volume espresso in
.
Si definisce:
In particolare indica il tempo di vita medio di ricombinazione elettrone-lacuna dove, mediamente, ogni
nanosecondo un elettrone cade dalla banda di conduzione alla banda di valenza per ricombinarsi con la
lacuna emettendo un fotone di energia pari a
. Quindi un fotone viene emesso ogni
.
Inoltre si indica:
Ed infine:
Pertanto si dimostra che vale la seguente uguaglianza:
Allora si ricava la densità di elettroni/lacune in funzione di un determinato livello energetico :
125
Dove:
Pertanto, all’aumentare di
(al diminuire di
(diminuisce) la densità di trovare elettroni
).
126
) fissato un valore di
(di trovare lacune
(livello energetico) aumenta
) , aumentando di conseguenza
Si definisce ora:
che rappresenta il guadagno netto di
angolare .
Inoltre:
fissato una pulsazione
Sapendo che:
è un qualsiasi livello energetico in banda di conduzione;
è un qualsiasi livello energetico in banda di valenza.
Quindi dal punto di vista fisico il guadagno netto
è proporzionale al numero di stati occupati in banda
di conduzione a energia
per il numero di stati vuoti in banda di valenza a energia
[emissione
stimolata] meno il numero di stati occupati in banda di valenza a energia
per il numero di stati vuoti in
banda di conduzione a energia
[assorbimento]:
Quindi:
Dove:
Quindi:
Ricaviamo, ora, per quale valore di
127
si ha che il guadagno sia
, esplicitando la tensione:
Quindi si ricava:
Cioè otteniamo:
Sostituendo con le funzioni:
e approssimando:
Ribaltando entrambe le espressioni:
Applicando il logaritmo naturale ad entrambi i membri otteniamo:
Dove sapendo che:
Otteniamo che:
Quindi se
si ha guadagno nullo,
, in quanto la densità degli stati
è rigorosamente
nulla e, pertanto, si è nel band gap. Cioè per
e, di conseguenza,
non si crea l’inversione
di popolazione.
Se
si è realizzata l’inversione di popolazione (gli elettroni dalla banda di valenza vanno in banda di
conduzione, lasciando così delle lacune in banda di valenza), cioè la densità di elettroni al livello energetico
superiore è maggiore della densità di elettroni al livello energetico inferiore.
Difatti si ricava:
128
Cioè otteniamo:
Sostituendo con le funzioni:
e approssimando:
Ribaltando entrambe le espressioni:
Applicando il logaritmo naturale ad entrambi i membri otteniamo:
Dove sapendo che:
Otteniamo che:
Da questa condizione scaturisce la ‘regola di progetto’ per realizzare il laser, ovvero:
Quindi il diodo e la f.e.m.
equilibrio).
Inoltre si osservi che:
servono proprio a realizzare l’inversione di popolazione (sistema fuori-
Pertanto:
si è nel bandgap in quanto la densità degli stati è nulla.
Mentre:
129
in questo caso domina l’assorbimento di fotoni in quanto l’elettrone assorbe il fotone per passare in banda di
conduzione.
Si noti che per
gli elettroni non si trovano in banda di conduzione ma in banda di valenza (sistema
all’equilibrio – assenza di inversione di popolazione).
Si dimostra che le curve di
in funzione di dove
sono del tipo:
è
à
Aumentando
significa
aumentare la f.e.m. ai capi del diodo
Si è in condizione di perdita
Non si è creata l’inversione di popolazione
La frequenza di picco, , si sposta verso destra all’aumentare di
Per concludere definiamo:
.
Con:
rappresenta un coefficiente tipico del materiale
rappresenta la densit di elettroni in condizioni di trasparenza. Anch’essa è una caratteristica del
materiale in quanto dipende dal band gap
In conclusione, l’espressione di
è di notevole importanza in fase di progetto in quanto per realizzare
(e quindi dimensionare) un laser le curve negative non hanno alcuna importanza ai fini progettuali e, quindi,
vengono considerate solo le curve che presentano dei picchi con valori di
, con
.
-
Rate Equations dei Laser
130
Indichiamo con:
Dove:
rappresenta la velocità di gruppo dei fotoni
rappresenta il fattore di confinamento
rappresenta il numero di fotoni totali nel volume modale.
Pertanto il tasso di emissione stimolata
rappresenta il numero netto di fotoni stimolati per unità di
tempo, cioè esprime quanti fotoni per unità di tempo al netto vengono stimolati.
Mentre:
Dove:
volume della regione attiva
fattore di confinamento
Quindi si ricava:
Dove:
rappresenta la densità degli stati
rappresenta la probabilità di emissione stimolata
rappresenta la probabilità di assorbimento
Quindi l’integrale di
di tale che:
è dato dalla somma continua di tutti i possibili valori di
Pertanto se è noto sperimentalmente
si può ricavare
dalla relazione:
e
in funzione
Si ricava, ora, la Rate Equation dei laser che permette di comprendere (e di simulare) il comportamento
dinamico dei laser, cioè la sua evoluzione nel tempo.
Definiamo:
il numero di fotoni presenti nel modo laser (si intende la distribuzione del campo EM associato)
la densità di portatori (elettroni iniettati in banda di conduzione e lacune in banda di valenza)
Pertanto, la derivata temporale di , , permette di comprendere come varia il numero di fotoni presenti
nel tempo a causa delle perdite di propagazione all’interno della guida e per effetto delle perdite agli specchi
a causa dell’emissione stimolata e spontanea.
Quindi, formalizzando in forma analitica otteniamo la velocità di variazione del numero di fotoni
presenti nel modo laser nel tempo per effetti di dispersione:
Dove:
rate (tasso) di emissione stimolata di fotoni
rate (tasso) di emissione spontanea di fotoni
tempo di vita medio dei fotoni all’interno della cavit Fabry-Perot. Esso è dipendente dalle perdite
di propagazione e dalle perdite agli specchi
A questo punto si esplicita il rate di emissione stimolata in funzione del guadagno, dove:
Sapendo inoltre:
è esprimibile come:
Quindi:
Invece
è esprimibile come:
Dove:
è il tempo di ricombinazione elettrone-lacuna: esso è il tempo di vita medio per cui un elettrone può
ricombinarsi con una lacuna in modo da emettere un fotone in modo spontaneo.
131
rappresenta la frazione di fotoni che vengono emessi spontaneamente e che si accoppiano nel modo
laser. Pertanto il modo laser non è altro che un fascio di luce coerente.
volume modale.
In conclusione, l’equazione
diviene:
Si definisce la densità dei fotoni come:
Sostituendo tale uguaglianza in si ottiene la variazione di densità dei fotoni nel tempo presenti nel modo
laser all’interno della regione intrinseca del diodo pin soggetta a perdite di propagazione:
La densità di fotoni varia nel tempo in quanto c’è una sottrazione tra i termini di generazione e i termini di
perdite. In particolare, i termini di generazione dipendono dalla concentrazione di elettroni in banda di
conduzione; pertanto se si dovesse verificare la condizione di trasparenza in cui
il primo termine di
sarebbe nullo:
.
Affinché si possa risolvere l’equazione si deve essere a conoscenza di , cioè la densità di elettroni e
lacune in banda di conduzione e in banda di valenza, rispettivamente. E’ opportuno esplicitare che non
può essere assunto costante in quanto la densità dei fotoni varia nel tempo e, pertanto, essendo legato ad
varierà anch’esso nel tempo in quanto nel momento in cui viene emesso un fotone viene, di conseguenza,
perso un elettrone e una lacuna che si sono ricombinati.
Pertanto, l’equazione non può essere risolta se si assume costante.
Si definisce, quindi, l’equazione di bilancio per la densità di portatori (elettroni in banda di conduzione e
lacune in banda di valenza):
Dove:
carica dell’elettrone
spessore della regione intrinseca
è un termine di generazione in quanto, a causa della f.e.m., si ha la formazione di una densità di
corrente che spinge corrente nel diodo pin, dando così l’iniezione di portatori
Si noti nell’equazione
la differenza con il termine
la quale rappresenta il contributo
di perdite in quanto nel momento in cui c’è il decadimento di un elettrone in banda di valenza ove va a
ricombinarsi con una lacuna per emettere un fotone si ha la perdita di un elettrone in banda di conduzione e
di una lacuna in banda di valenza ed, inoltre, l’emissione spontanea contribuisce alla perdita di portatori.
132
Trattando da un punto di vista fisico l’equazione
portatori, pertanto il termine
, si è detto che
è il tempo di ricombinazione dei
fornisce la velocità di ricombinazione dei portatori a fronte di una densità di
portatori pari ad .
Nell’equazione , invece, si ha il termine
che esprime la velocità con cui un elettrone si ricombina con
una lacuna per emettere un fotone. Ma il fotone emesso deve accoppiarsi al modo laser che presenta un suo
fattore di confinamento di potenza ed, inoltre, si deve comprendere quanti fotoni emessi spontaneamente
danno contributo al fascio laser (cioè si accoppiano al modo laser) e ciò viene tenuto conto dalla quantità .
Questo spiega il perché il termine è presente nell’equazione mentre è assente nell’equazione .
Ricapitolando, il termine
punta ad una variazione della densità di fotoni fatta rispetto al tempo; quindi ci
vuole un termine che tiene conto della velocità di ricombinazione dei portatori (
), ma di tutti i fotoni emessi spontaneamente si devono considerare solo quelli che influenzano il
modo laser.
Si noti, inoltre, che nell’equazione compare il termine in quanto di tutta la potenza ottica è utile solo la
potenza ottica concentrata nella regione intrinseca (attiva).
Invece, nella equazione
non compare il termine in quanto qualsiasi fotone viene creato, sia
spontaneamente che in modo stimolato, c’è una ricombinazione elettrone-lacuna da comportare una
variazione di .
In definitiva, l’equazione si focalizza su tutti quei fotoni che fanno parte del modo laser e che stanno nella
regione intrinseca (attiva) in quanto sono proprio questi fotoni che danno la generazione di ulteriori fotoni;
mentre l’equazione
si focalizza sulla variazione di portatori in banda di conduzione e in banda di valenza.
Pertanto:
Le equazioni e
spiegano, in senso analitico e fisico, la dinamica della densità dei fotoni nel modo laser
e dei portatori iniettati.
Alla base di queste due equazioni fondamentali c’è un’ipotesi: oltre alla distribuzione del modo quasi-TE o
quasi-TM ci sono anche modi longitudinali (lungo la guida).
Pertanto si deve scrivere la prima equazione, , per ogni modo longitudinale ove, in questo specifico caso, il
laser emetterà due lunghezze d’onda e, pertanto, esso risulterà ‘sporco’, cioè non monocromatico (vedi figura
che segue):
133
Esistono tipi di laser DFB (Distributed FeedBack Bragg) e laser DBR (Distributed Bragg Reflector) in cui i
riflettori sono realizzati con dei reticoli alla Bragg che permettono il passaggio del laser a certe lunghezze
d’onda mentre riflette una certa lunghezza d’onda alla pulsazione
.
Se la f.e.m. è in continua, si dice che il laser è in CW (Contigue Wave) mentre se la f.e.m. è in alternata si
parlerà di laser PW (Pulse Wave).
Si ipotizzi, ora, di lavorare con un laser CW. In condizione di stazionarietà di avrà:
Pertanto, il sistema diviene:
Risolvendo il sistema esplicitando
Diagrammando
si ottiene (e approssimando
):
in funzione di :
Oltre il
la densità di fotoni aumenta fino alla saturazione. Fissando un valore di
delle oscillazione di rilassamento:
si ha un laser con
134
Si noti che la condizioni iniziale per un laser avente
risulta essere più bassa rispetto al picco e,
pertanto, molto vicino allo zero (rosso). Invece, nel caso il laser avesse
le oscillazioni sono vicine alla
condizione iniziale (blu).
Riprendendo in considerazione la cavità di Fabry-Perot, si è detto precedentemente che:
Dove è noto che la somma
è in funzione del tempo di vita medio dei fotoni .
Si vuole, ora, disporre la cavità di Fabry-Perot in condizione in cui non ci sia guadagno, cioè in condizione di
could cavity:
Graficamente si realizza:
Si ricava che:
Pertanto la variazione di energia è pari a:
Un fotone che viene messo nella cavità risente solo delle perdite, pertanto si enuncia:
Si vuole, ora, scrivere una Rate Equation per la cavità di Fabry-Perot:
Dove risolvendo l’equazione differenziale del primo ordine otteniamo:
Pertanto esplicitiamo:
135
Dove:
136
Quindi, ritornando al rapporto
possiamo scrivere:
Pertanto:
Mentre, sapendo che:
Mettendoli in uguaglianza si ottiene:
Risolvendo l’uguaglianza in modo da esplicitare
otteniamo:
Applicando ad entrambi i lati i logaritmi naturali:
Sapendo dall’analisi matematica che il logaritmo naturale non è altro che un logaritmo in base neperiana,
allora il logaritmo naturale di un numero esponenziale è pari ad uno
quindi:
Pertanto, isolando
otteniamo:
Inoltre, dalle proprietà dei logaritmi si sa che:
,
Quindi, nel nostro caso:
137
Sapendo che:
In conclusione:
Il tempo di vita medio dei fotoni presenti nella cavità è in funzione della velocità di gruppo
delle perdite
per propagazione e agli specchi.
e della somma
138
Appunti di DISPOSITIVI ELETTRONICI PER I
SISTEMI INFORMATIVI
Per il Corso di Laurea in Ingegneria dell’Informazione
- PARTE 8 –
- MODULATORE ELETTRO-OTTICO DI MACH-ZEHNDER -
- L’interferometro di Mach-Zehnder come modulatore ottico
Uno degli interferometri più frequentemente utilizzato è il famoso tipo Mach-Zehnder.
La modulazione esterna, più complessa e costosa di quella interna, è migliore in termini di prestazioni, in
quanto limita al minimo gli effetti dovuti alla distorsione. Viene realizzata imprimendo sulla portante ottica
di un laser CW (ad onda continua) una modulazione di ampiezza, mediante un modulatore esterno.
Il modulatore di Mach-Zehnder è un modulatore di tipo elettro-ottico, ossia che sfrutta l’effetto elettro-ottico
lineare per cui le caratteristiche dielettriche, ad esempio l’indice di rifrazione, di alcuni materiali, possono
essere modificate dalla presenza di un campo elettrico.
Funzionamento: il modulatore Mach-Zehnder è costituito di un ingresso, accoppiato ad una fibra
ottica, che si “sdoppia” in due bracci a forma di Y. La potenza in ingresso viene suddivisa in due parti uguali,
una per ogni braccio; se non viene applicato nessun campo elettrico al cristallo, i due raggi che attraversano
il dispositivo sono in fase, per cui all’uscita del modulatore si ritrova la stessa ampiezza di segnale
dell’ingresso (condizione di ON). Quando, invece, viene applicata una opportuna tensione, il cristallo cambia
il suo indice di rifrazione in modo tale che il raggio che attraversa il braccio su cui è applicato il campo
risulti sfasato di ; in questo caso all’uscita del modulatore avremo potenza 0, ottenendo la condizione di
OFF.
Graficamente il modulatore Mach-Zehnder è mostrato in basso:
In sostanza, il modulatore Mach-Zehnder è un modulatore elettro-ottico che modula la portante ottica usando
come modulante un segnale elettrico.
139
Vediamo nel dettaglio il suo funzionamento:
140
Il modulatore Mach-Zehnder viene impiegato in quanto permette di trasformazione una modulazione di fase
in una modulazione di ampiezza.
Il percorso geometrico della parte inferiore è identico al percorso geometrico della parte superiore essendo
l’unione di due rami ad Y, pertanto in fase di progetto ciò che deve essere dimensionato è la lunghezza
mentre l’angolo assume valori molto piccoli.
Si definisce il percorso geometrico per il fascio inferiore e superiore come:
Quando si combinano i fasci (presentano entrambi la stessa fase) si è in condizione di interferenza costruttiva
in quanto lo sfasamento tra i fasci è nullo.
L’angolo della giunzione deve essere necessariamente molto piccolo in quanto può fungere da sorgente di
fronti d’onda in quanto la forma geometrica ad Y le permette di comportarsi come antenna e, quindi, con il
susseguirsi di perdite per radiazione. Pertanto è necessario che il cambio di direzione di propagazione
(l’angolo ) sia il meno brusco possibile in modo da poter trascurare le perdite dovute ad un fenomeno di
radiazione per emulazione d’antenna. Quindi, si deve dimensionare opportunamente affinché le code dei
modi che si propagano siano distanti evitando che si accoppino:
Supponiamo che il ramo superiore induce una variazione di indice di rifrazione
(superiore) avrà percorso geometrico pari a:
Mentre il ramo DOWN (inferiore):
Accade che il ramo UP
Pertanto lo sfasamento sarà dato da:
Quindi lo sfasamento è dato da:
Dove:
Quindi si avrà interferenza distruttiva o intermedia a seconda di
, ed è proprio per questo che il
modulatore Mach-Zehnder trasforma la modulazione di fase in modulazione di ampiezza. Pertanto, pilotando
opportunamente
con una tensione elettrica esterna si può ottenere in uscita o un valore logico alto (1)
o un valore logico basso (0).
Si suppone che i campi elettrici viaggianti, rispettivamente, sul ramo UP e sul ramo DOWN sono:
Pertanto il campo elettrico totale uscente dal modulatore è pari a:
Mentre il suo complesso coniugato è pari a:
Quindi la potenza di uscita dal modulatore è dato dal prodotto:
Sapendo, inoltre, che:
Otteniamo:
141
In conclusione, si è ricavato il rapporto di potenza tra la potenza di uscita dal modulatore e quella d’ingresso
al modulatore stesso:
Pertanto nel caso in cui
non si è prodotta la massima variazione:
, (dimensionando opportunamente
si ha:
, mentre se
, cioè
. In questo caso specifico,
,
si è realizzata la modulazione di ampiezza semplicemente effettuando una modulazione di fase pari a 180°
attraverso l’applicazione di un campo elettrico agli elettrodi, dove la tensione genera uno sfasamento nullo
mentre a tensione si ha uno sfasamento di 180°, come mostrato nel diagramma in basso:
Con che rappresenta il coefficiente elettro-ottico.
Attualmente i modulatori elettro-ottici vengono realizzato mediante l’effetto plasma.
Pertanto la variazione di indice del Si (silicio) a seguito di una concentrazione di cariche libere è data da:
Pertanto:
E’ possibile variare
cambiando (per effetto plasma) la concentrazione dei portatori di banda di
conduzione e in banda di valenza. Quindi
sarà:
142
143
Appunti di DISPOSITIVI ELETTRONICI PER I
SISTEMI INFORMATIVI
Per il Corso di Laurea in Ingegneria dell’Informazione
- PARTE 9 –
- MEMORIE IN SCALA NANOMETRICHE -
-
DRAM con materiali ad elevata permettività
La semplice cella DRAM è composta da un transistore come switch (porta di trasmissione) ed un
condensatore come elemento di carica.
La versione più ridotta di cella di memoria dinamica per DRAM è quella detta cella a un transistore che
impiega un solo MOS e una capacità per bit di memoria secondo lo schema di principio riportato in basso.
-
SCRITTURA: si carica alla Bit Line il livello logico desiderato (ad esempio il livello logico alto (1)
– ad una tensione pari a ) e la Word Line viene abilitata in maniera tale da rendere la porta di
trasmissione T aperta. Di conseguenza, essendo la porta di trasmissione T aperta funge da circuito
aperto e la tensione presente sulla Bit Line andrà a caricare la sola capacità di memoria ad una
tensione pari a . Quindi l’informazione è memorizzata in .
- LETTURA: supponendo che inizialmente nella capacità è precaricata l’informazione attraverso
l’operazione di scrittura (tensione ai capi di pari a ), è possibile leggere il dato in memoria
disabilitando la Word Line dove provvederà a chiudere la porta di trasmissione T e, quindi, avviene
il trasferimento di carica tra e . A seguito della distribuzione di carica, su entrambi le capacità
saranno presenti le tensioni .
Si noti che scalando l’intero sistema si ha che anche la tensione
sarà scalata con una conseguente
riduzione e, pertanto, anche la carica in sarà ridotta lasciando inalterate le dimensioni fisiche di .
Questo dimostra che per poter realizzare nuove generazioni di DRAM (ad elevate prestazioni) non c’è alcun
bisogno di variare la capacità di memoria .
E’ possibile esprimere la capacità del condensatore nella forma:
Dove:
l’area totale del condensatore (definito dall’area della superficie dell’elettrodo inferiore);
spessore fisico del dielettrico;
permettività dielettrica relativa del materiale utilizzato;
permettività dielettrica del vuoto.
Ricapitolando, cambiando generazione e, quindi, utilizzando un dielettrico avente minore dell’ossido di
silicio,
, allora lo spessore fisico del dielettrico
diminuisce facendo aumentare conseguentemente la
capacità di memoria ma, data la limitazione di progetto in cui deve rimanere costante, allora si ovvia a
tale limite aumentando l’area del condensatore
migliorando, così, la capacità del condensatore.
Si noti che nell’evoluzione prestazionale delle DRAM sono stati utilizzati i seguenti dielettrici:
Affinché si possano migliorare le prestazioni delle DRAM si deve operare su due aspetti:
1. Aumentare la costante di permettività del dielettrico;
2. Ridurre l’area di occupazione superficiale del chip.
La seconda opzione viene risolta riducendo l’occupazione superficiale del chip attraverso lo sviluppo del
dispositivo in verticale comportando, conseguentemente, una riduzione di area.
144
Questo si traduce in due tipi di tecnologie differenti:
DRAM A TRENCH CAPACITOR:
145
In questa struttura la superficie della capacità viene notevolmente incrementata agendo in senso verticale
alla superficie del dispositivo, e cioè scavando una trincea profonda nella quale viene depositato sia l’ossido
sottile (dielettrico), che il polisilicio che costituisce l’armatura del condensatore. Questa struttura viene
denominata ‘trench capacitor’ con riferimento alla trincea scavata nel silicio con attacco selettivo in plasma.
DRAM A STACKED CAPACITOR:
Nella tecnologia a trench capacitor si utilizza, ad esempio, un processo a
risoluzione possibile) utilizzando un dielettrico di tipo ON, con
.
Si stima che la larghezza del dispositivo sia pari a:
(che rappresenta la minima
Mentre l’area occupata superficialmente dalla è:
Ed, infine, la profondità della trincea è pari a
con una occupazione di area pari a
.
Alla termine del progetto si nota che il rapporto a
è molto basso e, pertanto, il dispositivo risulta
essere molto profondo rispetto alla larghezza dando così una condizione non ottimale.
Pertanto si ovvia a tale problema realizzando le DRAM con costanti di permettività ad elevata
permettività
in maniera tale da realizzare più facilmente i processi di trench/stacked.
Un materiale con è, ad esempio, il:
Di seguito sono elencati i requisiti più rilevanti per l’utilizzo del dielettrico con una permettività elevata da
integrare in un condensatore di una cella DRAM:
- Elevata permettività (
per garantire più semplici geometrie dell’elettrodo;
- Il materiale deve essere depositato in modo omogeneo come un film sottile con uno spessore
su aree larghe (wafer da 12”). La temperatura dovrebbe essere la più bassa possibile.
- Quando i tempi di lettura e scrittura si avvicinano a
, il comportamento dielettrico non dovrebbe
mostrare una significativa dispersione fino a frequenze di pochi GHz;
Sono desiderabili tempi di refresh dell’ordine di ;
La stabilità a lungo termine delle proprietà (almeno per 10 anni di vita) è indispensabile;
Tutti i processi per lo stesso materiale dielettrico devono essere compatibili con la tecnologia
CMOS.
I materiali ad alta permettività come il BST sono dielettrici non lineari, cioè la polarizzazione indotta ha una
dipendenza non lineare dal campo applicato:
-
Come mostrato in figura in basso:
Si noti che appena aumenta il campo
si esce dalla regione lineare.
Infine, la dipendenza della permettività dalla temperatura per un film sottile di BST è riportata in figura in
basso.
Si noti che anche
Dove
varia in funzione della temperatura secondo la Legge di Weiss:
146
-
RAM ferroelettriche (FeRAM)
Un recente tipo di dispositivo di memoria è la RAM ferroelettrica (FeRAM) che include un film
ferroelettrico come condensatore per conservare i dati. Il film ferroelettrico ha una caratteristica con isteresi
e, quindi, una polarizzazione residua che può essere annullata applicando un campo elettrico apposto.
La FeRAM utilizza la caratteristica polarizzazione-campo elettrico, P-E, con isteresi per mantenere i dati in
una configurazione non volatile e consente una riscrittura dei dati veloce e frequente.
Quindi, la FeRAM ha le caratteristiche vantaggiose sia della RAM che della ROM.
Tensioni impulsive sono usate per scrivere e leggere l’informazione digitale. Se il campo elettrico
dell’impulso applicato è nella stessa direzione della polarizzazione residua non si verifica commutazione
(vedi figura in basso).
Le dimensioni delle FeRAM entrano nell’ordine dei metri e, quindi, garantisce tensioni di funzionamento
inferiori rispetto alla tensione di alimentazione.
Le quantità
e
sono chiamati punti di polarizzazione residua.
A tensione applicata nulla si è in
. Applicando una tensione maggiore di zero si giunge al punto
subendo una variazione
portandoci, così, in condizione di no switching.
Se invece lo stato iniziale fosse stato
e si fosse partiti da
a fronte di una tensione maggiore di zero
allora si subisce una variazione
portandoci, così, in condizione di switching.
Si può definire
come variazione di carica in condizione di switching e
come variazione di carica
in condizione di no switching:
La differenza della carica
Vediamo a livello circuitale:
( è l’area del condensatore) consente di distinguere i due stati logici:
147
Dove:
148
condensatore ferroelettrico;
capacità parassita della bit line.
Scrittura “0” logico: la Drive Line è a
che è maggiore di zero mentre la Bit Line và a 0V quindi la Word
Line viene indiizzata (MOS conduttivo).
Poiché la Bit Line è posta a 0V, la
sarà presente ai capi di
sottoforma di
impulso. In conclusione lo “0” logico corrisponde ad un alto picco di tensione su
.
Scrittura “1” logico: la Bit Line và a
mentre la Word Line è abilitata e la Drive Line va a 0V.
Pertanto su
comparirà una tensione pari a
invertita rispetto a prima.
Lettura: la Bit Line viene disabilitata (floating) mentre la Drive Line và a
Sense Amplifier è pari a:
I valori di
Con:
e
sono, rispettivamente, riferiti ai valori assunti da
e la tensione che giunge al
alla lettura di “0” logico e “1” logico.
Otteniamo:
In conclusione, cambiando il valore della capacità
cambia il valore della tensione che viene letta.