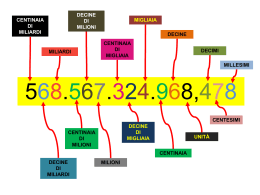
di Gemma Gallino e Stefania Serre
Per non essere intimoriti dalla matematica
è importante ricordare che la specie umana
ha impiegato secoli o addirittura millenni
per orientarsi attraverso la nebbia
delle difficoltà e dei paradossi,
che ora i nostri insegnanti
ci invitano a risolvere in pochi minuti
Un allievo perspicace
osso di lupo preistorico
La scrittura dei numeri
Sacerdoti Egizi intenti a
registrare le quantità di
grano prodotte
N° buoi: 400.000
N° capre: 1.422.000
N° prigionieri: 120.000
×2
×2
×2
1
25
2
4
50
100
8
200
×2
×2
×2
1
25
2
4
50
100
8
200
14
350
14 = 2 + 4 + 8
50 + 100 + 200 = 350
×2
×2
1
7
2
14
28
4
×2
×2
1
7
2
4
14
28
6
42
42 = 14 + 28
2+4=6
1
9
1
6
2
18
36
2
4
12
24
8
48
9
54
4
5
45
“ Un padre possedeva 11
cammelli e morendo
disponeva che così
venissero divisi: la metà di
tutti quanti al figlio
maggiore, un quarto al
secondo figlio, e un sesto
al figlio minore. Quando
morì i figli si chiesero come
fosse possibile eseguire le
disposizioni del padre dal
momento che un cammello a
metà valeva ben poco.
1 1 1
  
2 4 6
E non
12
12
63 2

12
cioè l’intera eredità
11

12
Zigurrat, cioè torri Babilonesi
utilizzate come osservatori
astronomici
sessagesimale: con base 60
posizionale: un simbolo cambia di valore
secondo la posizione
incompleto: manca un simbolo per 0
e per molte altre cifre.
12  2
22  4
32  6
42  8
5  2  ...
6  2  ...
7  2  14
8  2  ...
9  2  ...
10  2  ...
11  2  ...
12  2  ...
13  2  ...
14  2  ...
15  2  ...
16  2  ...
17  2  ...
18  2  ...
19  2  38
20  2  40
30  2  1
40  2  1;20
50  2  1;40
57  2  ?50  7   2 
 50  2   7  2 
 1;40  14  1;54
25
16
9
4
1
32 - 22 = 5
42 - 3 2 = 7
52 - 42 = 9
1 + 3 = 22
1 + 3 + 5 = 32
1 + 3 + 5 + 7 = 42
Metodo additivo
Metodo sottrattivo
Metodo moltiplicativo
106
105
104
103
Cartesio
102
Discours sur la methode
1650
10
1
Romani pueri longis rationibus assem discunt
in partis centum diducere.
” Dicat filuis Albini:
si de quicunce remota est uncia, quid superat?
poteras dixisse”
“ tiens”
“eu!! rem poteris servare, redit uncia, quid fit? “
“semis”
Orazio, Ars poetica, vv. 325-30.
Per noi è facile!
5 1
 
12 12
4 1

12 3
5 1
6 1

 
12 2
12 12
Con le dita ……
….o con l’abaco…
“Pythagorici vero, ut in omnibus rebus
erant ingeniosissimi et subtilissimi,
descripserunt sibi quandam
formulam, quam ob honorem sui
praeceptoris,
mensam Pytagoream nominabant; a
posterioribus appellatur abacus”
“ Pytagorici vero hoc opus
(abacum ) composuerunt ut ea que
magistro suo Pitagora docente
audierant, ocul subiecta retinerent
et firmius custodirent”
6
5
12
261
15
257 +174
174
257
257 +174
=431
174
257
Anno 346 Cedi, cioè 595 d. C.
4
1
?
2
3
= 2×601 + 32 = 152
= 2×602 + 0×601 + 32 = 7232
base 20
39 = 19 + 20
84 = 4×20 + 4
unità, centinaia, decine di migliaia…
decine, migliaia, centinaia di migliaia…
= 12
= 102
unità, centinaia, decine di migliaia…
decine, migliaia, centinaia di migliaia…
= 14.700
= 147
Muhammad ibn Musà
al-Khuwarizmi - 800
“ Se dopo aver sottratto non resta nulla, scrivete un
cerchietto altrimenti il posto rimane vuoto.
Il cerchietto deve occupare il posto, altrimenti vi sono
meno cifre e così, ad esempio, la seconda può essere
scambiata per la prima. »
Fibonacci
Liber Abaci – 1 202
Quot paria coniculorum in uno anno
ex uno pario germinentur?
1
2
3
4
5
6
7
8
9
10
2
4
6
8
10
12
14
16
18
20
3
6
9
12
15
18
21
24
27
30
4
8
12
16
20
24
28
32
36
40
5
10
15
20
25
30
35
40
45
50
6
12
18
24
30
36
42
48
54
60
7
14
21
28
35
42
49
56
63
70
8
16
24
32
40
48
56
64
72
80
9
18
27
36
45
54
63
72
81
90
10
20
30
40
50
60
70
80
90 100
Mensa
pitagorica
Algebristi - Algoristi
Tally utilizzato in
Inghilterra