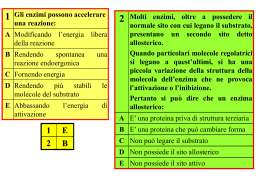
Corso di “Modellistica dei Sistemi
Biologici”
A.A. 2008/09
Cinetiche di Reazione
Docente: ing. Carlo Cosentino
Lab. di Biomeccatronica
E-mail: [email protected]
Tel: 0961-369-4051
URL: http://bioingegneria.unicz.it
http://wpage.unina.it/carcosen
Università degli Studi Magna Græcia di Catanzaro
I anno – II semestre CdL specialistica in Ingegneria Biomedica
Corso di Modellistica di Sistemi Biologici – Ing. C. Cosentino – A.A. 2008/09
1
Equilibrio e Velocità di Reazione
 L’equilibrio è legato alla variazione di energia biochimica
libera standard, ∆G’°
 La velocità della reazione, invece, è determinata dall’energia
di attivazione, ∆GS‡→ P
2
Equilibrio di Reazione
k1
S →
P
 Si consideri la semplice reazione reversibile
S ←
P
k −1
 Essa può essere descritta dal sistema di eq.
d [S ]
= − k1 [S ] + k −1 [P ]
[P] = k1
dt
′ =
K eq
d [P ]
[S ] k−1
= k1 [S ] − k −1 [P ]
dt
 Dalla termodinamica, si ha che la costante di equilibrio
′
∆G′° = − RT ln K eq
R (costante dei gas) = 8.315 J/mol·K
T (temperatura assoluta) = 298 K (25 °C)
3
Velocità di Reazione
 La velocità della reazione è determinata da
 concentrazione dei singoli reagenti
 una costante cinetica, in genere indicata con k
k
→
P la velocità di reazione è
 Ad es. la reazione S 
V = k [S ]
 Dalla teoria dello stato di transizione si ha
kT − ∆G RT
k=
e
h
dove k e h sono la costante di Boltzmann e Planck
rispettivamente
‡
4
Cinetica Enzimatica
 Gli enzimi sono una tipologia di proteine specializzate nella
catalisi delle reazioni
 I catalizzatori non reagiscono, ma favoriscono la reazione
diminuendo la soglia di energia necessaria alla formazione del
prodotto
 Nel caso degli enzimi questo
avviene tramite la formazione di un
composto enzima-substrato, da cui
poi il substrato viene trasformato
nel prodotto finale della reazione
5
Ruolo degli Enzimi
 Gli enzimi giocano un ruolo chiave in tutti i processi
biologici
 Essi hanno un ruolo importante nella regolazione delle vie
metaboliche
 Molte malattie sono causate dalla carenza o assoluta
mancanza di enzimi
 Molti farmaci agiscono interagendo con gli enzimi
6
Enzimi: Funzionamento
 Le reazioni catalizzate da enzimi
avvengono in una ansa chiamata sito
attivo in cui si formano condizioni
favorevoli alla reazione
 La molecola che si lega al sito attivo viene
chiamata substrato
 La superficie del sito attivo viene delineata
da amminoacidi i cui residui legano il
substrato e ne catalizzano la
trasformazione
7
Reazione di Michaelis-Menten
 Il modello base di reazione enzimatica è stato proposto
da Michaelis e Menten nel 1913
dove k 1, k -1, k 2 sono costanti positive associate ai tassi
di reazione
L. Michaelis (1875-1949)
 La legge di azione di massa ci dice che il tasso di
reazione è proporzionale al prodotto della
concentrazione dei reagenti
A+ B 
→ C
k
d [C ]
= k [A][B ]
dt
M. Menten (1879-1960)
8
Reazione di Michaelis-Menten
 Dalla reazione ricaviamo il seguente modello
s = −k1es + k −1c,
e = −k1es + (k −1 + k 2 )c
c = k1es − (k −1 + k 2 )c,
p = k 2 c
dove abbiamo indicato le concentrazioni delle varie specie
come s := [S ], e := [ E ], c := [ES ], p := [P ]
e le condizioni iniziali sono s(0)=s0, e(0)=e0, c(0)=0, p(0)=0
 Si noti che l’eq. di p è disaccoppiata dalle altre e fornisce
t
p(t ) = k 2 c(τ )dτ
∫
0
9
Modello Semplificato
 La quantità totale di enzima, libero più legato, rimane
invariata nel tempo, come si può vedere anche sommando la
seconda e terza eq.
e + c = 0 ⇒ e(t ) + c(t ) = e0
per cui possiamo derivare e(t) e sostituire, ottenendo il
sistema semplificato in due equazioni
s = −k1e0 s + (k1s + k −1 )c,
c = k1e0 s − (k1s + k −1 + k 2 )c,
s (0 ) = s0
c(0 ) = 0
10
Modello Semplificato
 Tipicamente la formazione iniziale del complesso ES è molto
veloce, dopodichè rimane all’equilibrio
 Ciò si traduce nell’assumere dc/dt ≈ 0, da cui
e0 s(t )
c(t ) =
s(t ) + K m
k 2 e0 s
⇒ s = −
s + Km
dove la costante positiva
k −1 + k 2
Km =
k1
è detta costante di Michaelis-Menten
11
Approssimazione di Pseudo-Regime
 La quantità di enzima si assume tipicamente piccola rispetto
a quella di substrato, per cui quest’ultima rimane pressoché
invariata durante la formazione del complesso  s(0)=s0
 Dall’eq. di s otteniamo la soluzione implicita
s(t ) + K m ln s (t ) = s0 + K m ln s0
 Si noti che l’eq. di c(t) non soddisfa la cond. iniz. c(0)=0, ma
l’approssimazione vale in molti casi
 Esistono due scale temporali, una corrispondente alla
formazione del complesso, l’altra relativa alla trasformazione
del substrato
12
Validità dell’Approssimazione
 Per stabilire il range di validità del modello approssimato
dobbiamo rispondere a diverse domande
 Quanto è veloce il transitorio iniziale?
 Per quali valori di parametri sono sufficienti le approssimazioni
di pseudo-regime?
 Cosa accade se la concentrazione di enzima non è
effettivamente piccola rispetto a quella di substrato?
13
Adimensionalizzazione
 Per rispondere alle domande precedenti dobbiamo
innanzitutto adimensionalizzare il sistema, mediante le
trasformazioni
s(t )
c(t )
, v(τ ) =
,
τ = k1e0t , u (τ ) =
s0
e0
e0
k2
k −1 + k 2 K m
, K=
, ε=
=
λ=
k1s0
k1s0
s0
s0
 Che è una scelta ragionevole se ε <<1, ossia quando l’enzima
è presente in quantità molto minore del substrato
14
Adimensionalizzazione
 Utilizzando le trasformazioni precedenti otteniamo il sistema
u = −u + (u + K − λ )v, u (0 ) = 1
ε v = u − (u + K )v,
v(0 ) = 0
si noti che K-λ>0
 Non è possibile ricavare una
soluzione analitica, ma si può
abbozzare l’andamento
studiando il segno delle derivate
al variare di u
15
Stima del Transitorio
 Sfruttando il fatto che s0 non varia apprezzabilmente durante il
transitorio iniziale si può valutare la durata di questo dall’eq. di c
c = k1e0 s0 − k1 (s0 + K m )c
 La costante di tempo associata a questo sistema del primo ordine è
1
tc =
k1 (s0 + K m )
 Una stima della durata della dinamica di s si ottiene considerando la
derivata massima
s0
s0 + K m
ts ≈
≈
ds dt max
k 2 e0
16
Stima del Transitorio
 Sulla base delle stime effettuate, la condizione che il transitorio iniziale sia
molto veloce rispetto alla dinamica della trasformazione del substrato,
ossia tc<<ts si riscrive
k 2 e0
k1 (s0 + K m )
2
<< 1
 Un’altra condizione per la validità dell’approssimazione è che la
deplezione di S durante il transitorio iniziale sia una frazione trascurabile
del totale, ossia |∆s/s0|<<1
ε=
e0
<< 1
s0 + K m
 La condizione precedente si ottiene considerando una stima per eccesso
di ds/dt, derivabile dalla eq. nel modello del 2° ordine (v. lucido 10)
∆s ≤
1
ds
tc = k1e0 s0 ⋅
dt max
k1 (s0 + K m )
17
Condizione di Pseudo-Regime
 Si noti, tuttavia, che il primo vincolo si può riscrivere come
k 2 e0
e0
1
=
⋅
<< 1
2
s0 + K m 1 + (k −1 k 2 ) + (s0 k1 k 2 )
k1 (s0 + K m )
 Il secondo vincolo risulta, pertanto, più stringente e può essere
considerato come condizione di validità dell’approssimazione di pseudoregime
 Si noti inoltre che, anche se e0/s0=O(1), l’approssimazione rimane valida
se Km è grande
18
Parametri Sperimentali
 Nella pratica sperimentale si misurano due parametri
 La costante di Michaelis-Menten
 La velocità massima di reazione Q = [R0 ]max = k 2 e0
k 2 e0 s0
Qs0
R0 =
=
s0 + K m s0 + K m
19
Substrato Suicida
 Un processo enzimatico di particolare importanza è quello
descritto dal modello di Walsh (1978)
dove E, S, P sono rispettivamente enzima, substrato e prodotto,
X, Y sono prodotti intermedi, Ei è l’enzima inattivato e le k sono
costanti positive
 Il rapporto r:=k3/k4 è chiamato coefficiente di partizione
20
Substrato Suicida
 S viene detto substrato suicida ed è capace di legarsi al sito attivo
dell’enzima come un comune substrato
 L’enzima lo converte in un inibitore che inattiva in maniera irreversibile
l’enzima stesso
 I substrati suicidi sono importanti perché forniscono un metodo per
inattivare uno specifico enzima
 L’uso principale è nella somministrazione di farmaci, perché non sono
dannosi nella forma comune e solo l’enzima specifico li può convertire
nella forma inibitoria (ad es. trattamento della depressione, epilessia,
alcuni tumori)
21
Substrato Suicida
 La cinetica dei substrati suicidi è stata studiata a fondo da Waley (1980) e
Tatsunami (1981)
 Questi studi si concentrano sul meccanismo che permette o meno al
substrato di essere interamente trasformato prima che tutto l’enzima sia
inattivato
 Waley ha concluso che questo dipende dal valore r e0 s0
 Tatsunami ha proposto come indice il valore
(1 + r ) e0
(1 + r ) e0
(1 + r ) e0
s0
s0 < 1
Tutto l’enzima è inattivato
s0 > 1
Il substrato viene trasformato interamente
22
Equazioni Cinetiche
 Applicando la legge di azione di massa
s = −k1es + k −1 x
e = −k1es + k −1 x + k 3 y
x = k1es − k −1 x − k 2 x
y = k 2 x − k 3 y − k 4 y
ei = k 4 y
p = k 3 y
e(0) = e0 , s (0) = s0 ,
x(0) = y (0) = ei (0) = p (0) = 0
23
Modello Ridotto
 Anche in questo caso si può sfruttare la conservazione della
quantità totale di enzima
e + x + y + ei = e0
e il fatto che l’eq. di p è disaccoppiata dalle altre
s = − k1 (e0 − x − y − ei )s + k −1 x
x = k1 (e0 − x − y − ei )s − (k −1 + k 2 )x
y = k 2 x − (k 3 + k 4 ) y
ei = k 4 y
 Studieremo il sistema risolvendo numericamente le eq.
24
Fenomeni Cooperativi
 Nel modello base abbiamo supposto che una molecola di
enzima si combini con una sola di substrato
 Molte proteine hanno più di un sito di legame, ad es.
l’emoglobina ha quattro siti per le molecole di ossigeno
 Una reazione tra un enzima e un substrato si dice
cooperativa se una singola molecola di enzima, dopo aver
legato una molecola di substrato ad un sito, può legarne
un’altra ad un altro sito
25
Effetto Allosterico
 Una tipologia di reazione cooperativa
molto importante si ha quando il
legame di un substrato ad un sito può
influenzare il legame di altri substrati
ad altri siti (enzima allosterico)
 Un substrato viene detto attivatore o
inibitore a seconda che aumenti o
diminuisca l’attività di legame in altri
siti
 Se la specie substrato funge anche da
modulatore l’interazione si dice
omotropica, altrimenti eterotropica
26
Esempio di Reazione Cooperativa
 Consideriamo ora un semplice esempio di reazione
cooperativa in cui un enzima ha due siti di legame
 Calcoliamo l’approssimazione a pseudo-regime e la funzione
di trasformazione del substrato
27
Equazioni Cinetiche
 Applicando la legge dell’azione di massa otteniamo
s = − k1se + (k −1 − k 3 s )c1 + k −3c2
c1 = k1se − (k −1 + k 2 + k 3 s )c1 + (k −3 + k 4 )c2
c2 = k 3 sc1 − (k −3 + k 4 )c2
e = − k1se + (k −1 + k 2 )c1
p = k 2 c1 + k 4 c2
s(0) = s0 , e(0) = e0 , c1 (0) = c2 (0) = p(0) = 0
 La conservazione dell’enzima fornisce
e + c1 + c2 = e0
28
Modello Ridotto
 Analogamente ai casi precedenti troviamo il modello ridotto
s = −k1e0 s + (k −1 + k1s − k 3 s )c1 + (k1s + k −3 )c2
c1 = k1e0 s − (k −1 + k 2 + k1s + k 3 s )c1 + (k −3 + k 4 − k1s )c2
c2 = k 3 sc1 − (k −3 + k 4 )c2
e adimensionalizziamo usando le relazioni
c1
c2
k −1
s
,
τ = k1e0t , u = , v1 = , v2 = , a1 =
k1s0
s0
e0
e0
k3
k
e
k2
k
a2 =
, a3 = , a 4 = − 3 , a5 = 4 , ε = 0
k1s0
k1
k1s0
k1s0
s0
29
Modello Adimensionale
 Sostituendo otteniamo
u = −u + (u − a3u + a1 )v1 + (a4 + u )v2
ε v1 = u − (u + a3u + a1 + a2 )v1 + (a4 + a5 − u )v2
ε v2 = a3uv1 − (a4 + a5 )v2
u (0 ) = 1, v1 (0 ) = v2 (0) = 0
 Come nei casi precedenti è possibile considerare a regime le
eq. relative a v1 e v2, ricavare queste quantità in funzione di u
e sostituire nella prima eq., ottenendo
u = −u
a 2 + a3 a5u (a 4 + a5 )−1
a1 + a 2 + u + a3u (a 4 + a5 )
2
−1
= −r (u ) < 0
30
Velocità Massima di Reazione
 Riportando in formato dimensionale troviamo la velocità di
reazione di Michaelis-Menten per e0/s0<<1
ds
R0 (s0 ) =
dt
dove
t =0
k 2 K m′ + k 4 s0
= e0 s0
K m K m′ + K m′ s0 + s02
k 4 + k −3
k −1 + k 2
Km =
, K m′ =
k1
k3
sono le costanti di Michaelis-Menten delle due reazioni
31
Curve di Hill
 La curva risultante può differire da quella di una reazione base,
come mostrato in figura
2
s
→
0
⇒
R
∝
s
 Ad es., per k2=0 si vede subito che
0
0
0
 In questo caso l’andamento viene
approssimato con una curva di
Hill
Qs0n
R0 (s0 ) = n
, n>0
n
s0 + K m
32
Curve di Hill
 Si noti che il numero n non è necessariamente intero, inoltre
si definiscono i seguenti casi
 n>1  cooperazione positiva
 n<1  cooperazione negativa
 n=1  cooperazione nulla
 Alla stessa relazione (ma con n intero) si arriva considerando
un modello di enzima che lega contemporaneamente n
molecole substrato, ossia E+nS E+nP
33
Autocatalisi
 Molti processi biologici hanno un meccanismo insito di
regolazione mediante retroazione (feedback)
 In pratica la regolazione si basa sul fatto che il prodotto di una
reazione può influenzare la storia futura del processo
 L’effetto di regolazione è generalmente nonlineare e può essere sia
di attivazione che di inibizione nei confronti della reazione
 In particolare l’autocatalisi è il processo per cui una specie viene
utilizzata nella reazione che la produce, ad es.
34
Esempi di Autocatalisi
 Se la concentrazione della specie A viene mantenuta
costantemente al livello a, possiamo scrivere
x = k1ax − k −1 x
2
⇒
k1a
x(t ) → x S =
k −1
 Il sistema ha due punti di equilibrio, x=0 instabile e x=xS
stabile
 La retroazione è fornita dal prodotto stesso, che inibisce la
formazione di ulteriore prodotto: l’intensità dell’azione
inibente cresce con il quadrato della concentrazione
 Il meccanismo è analogo a quello studiato nelle popolazioni
monospecie
35
Esempi di Autocatalisi
 Si consideri la reazione
e si supponga che a e b vengano mantenuti costanti
x = (k1a − k 2 b )x − k −1 x 2
 Il sistema ha una biforcazione quando k1a-k2b=0, infatti
 k 1a-k 2b>0  L’origine è un p. di equilibrio instabile, infatti il
tasso di produzione è maggiore di quello di trasformazione
 k 1a-k 2b<0  L’origine è un p. di equilibrio stabile , infatti il
tasso di produzione è minore di quello di trasformazione
36
Esempi di Autocatalisi
 Un ulteriore esempio di autocatalisi è il modello di oscillatore
biologico ideale proposto da Lotka
dove la concentrazione di A è mantenuta costante
 Si noti che le prime due reazioni sono autocatalitiche
 Applicando la legge dell’azione di massa riotteniamo le
equazioni di Lotka-Volterra
x = k1ax − k 2 xy
y = k 2 xy − k 3 y
37
Grafico di Lineweaver-Burke
 Il grafico di L-B, detto anche dei doppi reciproci, si ricava
invertendo ambo i membri dell’eq. della velocità di reazione
1 K m + [S ]
=
V0 Vmax [S ]
Km
1
1
=
+
V0 Vmax [S ] Vmax
38
Reazione Uni-Uni
 Reazione enzimatica unireactant-unireactant
E+S
k2
k
k
k
1→


←
ES
3→

←
k4
EP
5→

←
E+P
k6
VMr
VMf
[S ] − r [P]
f
Km
d [P ] K m
=
[S ] [P]
dt
1+ f + r
Km Km
[P]eq
K eq =
[S ]eq
VMf K Mr
= r f
VM K M
Relazione di Haldane
39
Reazione Bi-Bi
 Reazioni enzimatiche bi-substrate
Vmax
d [P ]
= S1 S 2
K s K m K mS1 K mS 2
dt
+
+
+1
[S1 ][S 2 ] [S1 ] [S 2 ]
Ordered Bi-Bi
40
Reazione Ping-Pong Bi-Bi
 In questo caso non avviene la formazione di complesso
ternario
V
d [P ]
= S1 max S 2
Km Km
dt
+
+1
[S1 ] [S 2 ]
N.B. Rispetto al caso precedente c’è
un parametro in meno
41
Bi-Bi vs Ping-Pong
 L’andamento nel tempo è simile
 La differenza si evince dal comportamento al variare della
concentrazione di S2
Bi-Bi Ordinata
Ping-Pong
42
Inibizione Enzimatica
 Inibizione Reversibile
 Competitiva
 Mista (non competitiva)
 Incompetitiva
 Inibizione Irreversibile
 e.g. substrato suicida
43
Inibizione Competitiva
 L’inibitore ed il substrato si legano allo stesso sito
Vmax [S ]
d [P ]
=
αK m + [S ]
dt
α = 1+
[I ] ,
KI
KI =
[E ][I ]
[EI ]
44
Inibizione Competitiva
45
Inibizione Incompetitiva
 Siti di legame differenti
 L’inibitore si lega solo al complesso ES
Vmax [S ]
d [P ]
=
dt
K m + α ′[S ]
α ′ = 1+
[I ] ,
K I′
K I′ =
[ES ][I ]
[ESI ]
46
Inibizione Incompetitiva
47
Competizione Mista
 Siti di legame diversi
 L’inibitore può legarsi sia a E sia a ES
Vmax [S ]
d [P ]
=
dt
αK m + α ′[S ]
α = 1+
α ′ = 1+
[I ] ,
KI
[I ] ,
K I′
[E ][I ]
[EI ]
[
ES ][I ]
′
KI =
[ESI ]
KI =
Se α= α’ l’inibizione viene detta non-competitiva
48
Competizione Mista
49
Dipendenza da altri Fattori
 Bisogna ricordare che le reazioni enzimatiche sono
fortemente dipendenti da altri fattori, e.g. pH e temperatura
50
Modelli Fenomenologici
 In molti casi reali di interesse non si conosce in maniera
dettagliata la lista di reazioni che genera un certo processo
biologico
 Più realisticamente si può ricavare sperimentalmente l’effetto
globale al variare di una specie o delle condizioni al contorno
 In questo caso non si può utilizzare l’approccio visto finora,
trasformando direttamente le reazioni in eq. differenziali
 Il modello, quindi, è costituito da opportuni termini
matematici che descrivono i vari fenomeni pur non
rappresentandone i meccanismi biochimici di base
51
Esempi di Modelli Fenomenologici
 Si consideri il seguente modello
a
− cu
b+v
v = du − ev
u =
con a, b, c, d, e costanti positive
 L’interpretazione biologica di queste eq. è che u attiva v, attraverso
un termine du , e entrambe u e v sono degradate in maniera
linearmente proporzionale alla loro concentrazione (si parla in
questo caso di cinetica del primo ordine)
 Il termine a/(b+v) porta in conto l’effetto di inibizione esercitato
da v su u, infatti il tasso di produzione di u è tanto più piccolo
quanto maggiore è la concentrazione di v
52
Esempi di Modelli Fenomenologici
 Il meccanismo di Thomas (1975) è stato sviluppato per
descrivere la reazione dei substrati ossigeno e acido urico in
presenza dell’enzima urease
u = a − u − ρR(u , v )
v = α (b − v ) − ρR(u , v )
uv
R(u , v ) =
1 + u + Ku 2
Effetto di inibizione del substrato
53
Esempi di Modelli Fenomenologici
 Un ulteriore modello di sistema attivatore (u) - inibitore (v)
u = a − bu +
(
u2
v 1 + Ku 2
)
v = u 2 − v
 L’attivatore u è un prodotto autocatalitico, come descritto
dal termine u 2/[v(1+Ku 2) ] , ma il tasso di produzione satura
al valore 1/Kv per u→∞
 L’inibitore v è attivato da u, ma ne inibisce la produzione
54