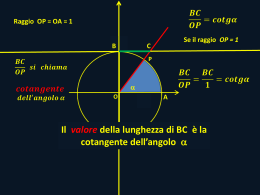
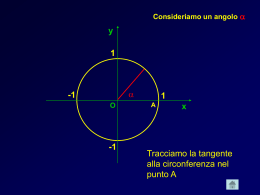
definite nella circonferenza goniometrica MAPPA Le funzioni goniometriche SENO COSENO COSECANTE SECANTE TANGENTE COTANGENTE LA FUNZIONE SENO Si dice seno di un angolo β l’ordinata del punto P associato a β nella circonferenza goniometrica. La funzione seno è limitata: può assumere valori compresi solo tra -1 e +1 periodica: si ripete sempre uguale ogni 360°; pertanto si dice che il suo periodo è di 360° o anche di 2 radianti LA FUNZIONE COSENO Si dice coseno di un angolo β l’ascissa del punto P associato a β nella circonferenza goniometrica La funzione coseno è limitata: può assumere valori compresi solo tra -1 e +1 periodica: si ripete sempre uguale ogni 360°; pertanto si dice che il suo periodo è di 360° o anche di 2 radianti LA FUNZIONE TANGENTE Si dice tangente di un angolo β l’ordinata del punto di intersezione tra il secondo lato dell’angolo, o il suo prolungamento, con la retta tangente alla circonferenza goniometrica nel punto in cui questa interseca il primo lato dell’angolo. La funzione tangente è illimitata: il suo campo di esistenza è R periodica: si ripete sempre uguale ogni 180°; pertanto si dice che il suo periodo è di 180° o anche di radianti La funzione tangente è uguale al rapporto tra le funzioni seno e coseno: tg β= sen β/cos β LA FUNZIONE COTANGENTE Si dice cotangente di un angolo β l’ascissa del punto di intersezione tra il secondo lato dell’angolo, o il suo prolungamento, con la retta tangente alla circonferenza goniometrica nel punto in cui questa interseca il semiasse delle ordinate positive. La funzione cotangente è illimitata: il suo campo di esistenza è R periodica: si ripete sempre uguale ogni 180°; pertanto si dice che il suo periodo è di 180° o anche di π radianti La funzione cotangente è uguale al rapporto tra le funzioni coseno e seno: co tg β= cosβ/sen β. Quindi la cotangente è il reciproco della tangente. LA FUNZIONE SECANTE La secante di un arco è il reciproco del suo coseno: sec = 1/cos . La funzione secante è illimitata: il suo campo di esistenza è R periodica: si ripete sempre uguale ogni 360°; pertanto si dice che il suo periodo è di 360° o anche di 2π radianti LA FUNZIONE COSECANTE La cosecante di un arco è il reciproco del suo seno: cosec = 1/sen. La funzione cosecante è illimitata: il suo campo di esistenza è R periodica: si ripete sempre uguale ogni 360°; pertanto si dice che il suo periodo è di 360° o anche di 2π radianti
Scaricare