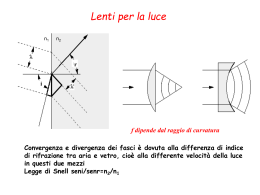
Telescopi: aberrazioni, ingrandimenti,
luminosità e risoluzione.
Paola Battaglia
Università degli Studi di Milano
Dipartimento di Fisica dello Stato Solido e Astrofisica
Telescopi
RIFRATTORE (con lenti)

RIFLETTORE (con specchi)

CATADIOTTRICO (con specchi e lenti)

1.Parametri principali:
1) il diametro D dell'ottica principale (lente o specchio), e dunque
il potere risolutivo del telescopio
1) la focale (pari alla distanza tra la lente e l'immagine se
l'oggetto si trova all'infinito)
2) la qualità dell'immagine in asse, cioè al centro del campo
visivo
3) la qualità dell'immagine fuori asse, cioè ai bordi del campo
visivo.
1/2
Telescopi
Il diametro e la focale spesso si esprimono con un rapporto
contenente al numeratore il diametro ed al denominatore la focale.
114/900, ad esempio,indica un telescopio di 114mm di diametro e
900mm di focale.
Obiettivi fotografici:
notazione leggermente
diversa. 200mm f/4 (oppure
200/4) indica un obbiettivo
da 200mm di focale, con
diametro di
200mm/4=50mm.
A volte per i telescopi si usa
una notazione identica, ma,
con significato diverso.
Infatti 200mm f/4 per un
telescopio significa 200mm
di diametro con focale
200mm*4=800mm.
2/2
Aberrazioni Ottiche
La qualità di un sistema ottico è determinato dalle aberrazioni
residue dell'immagine.

In assenza di diffrazione un sistema ottico perfetto produrrebbe
un immagine puntiforme sulla superficie focale (se la sorgente è un
punto).


Idealmente ciò avverrebbe sia sull'asse ottico che lontano da esso.
1/3
Aberrazioni Ottiche
Nella realtà, tuttavia, questo risultato
raramente viene ottenuto su tutta la
superficie focale anche quando ciò si
verifica sull'asse ottico.
Esistono diversi tipi di aberrazioni ed in
presenza di queste l'immagine di una
sorgente puntiforme diventa sfuocata e
prende il nome di figura di scattering.
La figura di scattering scaturisce da una
combinazione di aberrazioni, piuttosto che
da una sola.
E' difficile, dunque, capire da quale
aberrazione proviene una parte della figura
di scattering.
2/3
Aberrazioni Ottiche
Le aberrazioni ottiche possono essere divise in due classi principali:
MONOCROMATICHE, che si possono verificare sia in rifrattori
che riflettori e coinvolgono luce di una sola lunghezza d'onda
CROMATICHE, che si verificano quando le diverse lunghezze
d'onda si comportano in modo differente all'interno del sistema
ottico. Le aberrazioni cromatiche si presentano solo in sistemi che
contengono elementi rifrattivi (lenti).
3/3
Aberrazioni Monocromatiche
Le aberrazioni monocromatiche furono analizzate nel 1850 dal
matematico tedesco Ludwig Von Seidel e, per questo, sono anche
chiamate aberrazioni di Seidel. Von Seidel ha riconosciuto le
seguenti aberrazioni:
aberrazione sferica

coma

astigmatismo

curvatura di campo

distorsione

Delle aberrazioni di Seidel solo quella sferica è un'aberrazione
assiale (peggiora la qualità dell'immagine in asse). Tutte le altre
sono aberrazioni fuori asse ottico (sono visibili solo lontano dal
centro dell'immagine).
1/1
Aberrazione Sferica
I raggi luminosi paralleli
all'asse ottico che entrano nel
sistema a diverse altezze
vanno a fuoco in punti
differenti lungo l'asse stesso.
In una lente singola o in uno
specchio sferico i raggi più
esterni si intersecano in un
punto che è più vicino alla
lente o allo specchio rispetto
ai raggi interni. I raggi che
entrano molto vicini all'asse
ottico si intersecano nel fuoco
parassiale (F).
Ideale
Aberrazione Sferica
F
Asse Ottico
1/4
Aberrazione Sferica
L'aberrazione sferica può
essere:
1. positiva (raggi periferici molto
distorti)
1. negativa (raggi periferici poco
distorti)
A.S. ∝ D4/f3
fenomeno è accentuato nei sistemi che presentano un rapporto
focale corto!
2/4
Aberrazione Sferica
Una lente sferica ha un punto in cui non presenta aberrazione sferica
(aplanatico) situato a
Raplanatico = Rsfera/nlente
Esempio - Vetro Crown (basso
indice rifrazione, bassa
dispersione):
n = 1,5
solo il 43%
dell'area (67% del diametro) di
una lente sferica è utilizzabile.
Nei sistemi a lenti l'aberrazione sferica viene Lente Aplanatica
minimizzato usando combinazioni di lenti
concave e convesse o usando lenti asferiche (=
profili superficiali non sono porzioni di sfera o
3/4
cilindro).
Aberrazione Sferica
4/4
Coma
Fascio di luce obliquo:
l'intersezione dei raggi non
è simmetrica ma è spostata
rispetto l'asse del fascio.
I raggi luminosi fuori asse
passando attraverso la
lente vicino al bordo (raggi
marginali) intersecano la
superficie dell'immagine ad
altezze diverse rispetto a
quei raggi che passano dal
centro dell'apertura.
1/5
Coma
L'immagine risultante ha una forma simile a quella di una cometa
(un nucleo luminoso accompagnato da una coda).
Il coma è un'aberrazione piuttosto problematica: non solo
l'immagine fuori asse è poco brillante, ma risulta anche
asimmetrica.
Esempio: non è possibile misurare accuratamente la posizione
delle stelle su di una lastra fotografica ripresa con un sistema
affetto da coma.
2/5
Coma
2/5
Coma
Ernst Abbe scoprì una condizione in cui un sistema, libero anche
da aberrazione sferica, è privo anche di coma. La condizione è
nota con il nome di condizione del seno di Abbe:
“In un sistema privo di coma ogni raggio uscente proveniente da
un fascio di raggi parallelo all'asse ottico soddisfa la seguente
condizione
h/sinU' = C
dove h è l'altezza del raggio prima che entri nel sistema, U' è
l'angolo tra il raggio e l'asse ottico nel percorso verso il fuoco e
C è una costante.
4/5
Coma
Tra la pupilla d'entrata ed il piano focale esiste, dunque, una
superficie sferica immaginaria che connette i raggi entranti
paralleli ed i raggi di uscita con il suo centro in F, il fuoco.
Se questa superficie esiste ed il sistema non presenta
aberrazioni sferiche, tutte le distanze tra la superficie sferica
immaginaria ed F sono le stesse ed il sistema è perfettamente
simmetrico. La costante C è proprio il valore di questa distanza
ed un sistema che rispetta la legge del seno di Abbe si chiama
“aplanatico”.
5/5
Astigmatismo
In un sistema ottico affetto da astigmatismo i raggi luminosi che
propagano in due piani perpendicolari hanno fuochi differenti.
Se un sistema ottico affetto da astigmatismo venisse utilizzato
per formare l'immagine di una croce, le linee orizzontali e
verticali verrebbero messe a fuoco a distanze diverse e non
contemporaneamente.
1/2
Astigmatismo
Esistono due diverse forme di astigmatismo:
Il primo tipo si verifica per oggetti fuori dall'asse ottico. Può
essere presente anche quando il sistema ottico è perfettamente
simmetrico.

Il secondo tipo si verifica quando il sistema non è simmetrico
rispetto all'asse ottico. Può essere provocato da errori nella
lavorazione delle superfici o da un disallineamento delle
componenti. L'astigmatismo, in questo caso, può essere osservato
anche in raggi provenienti da oggetti in asse.

L'occhio umano spesso presenta questo secondo tipo di
aberrazione a causa di imperfezioni nella forma della cornea.
2/2
Curvatura di campo
L'immagine più brillante si forma su di un piano focale curvo
invece che su di un piano focale piano.
Se utilizzo una lastra
fotografica (che è piana)
l'immagine che ottengo è
sfuocata ai bordi. La maggior
parte delle lenti fotografiche
sono progettate per
minimizzare la curvatura di
campo e, dunque, hanno una
lunghezza focale che aumenta
con l'angolo del raggio.
1/1
Curvatura di campo
1/1
Distorsione
La distorsione non è propriamente un'aberrazione in quanto non
influenza la luminosità dell'immagine quanto piuttosto la sua
scala.
Distorsione “positiva”
= la scala dell'immagine
aumenta con la
distanza dall'asse
ottico. Le linee che non
passano per il centro
sono piegate
all'interno.
Spesso i binocoli presentano questo tipo di distorsione
1/3
Distorsione
Distorsione “negativa” = la scala dell'immagine diminuisce con la
distanza dall'asse ottico. L'effetto è quello di un'immagine che è
stata mappata su di una sfera.
2/3
Distorsione
“Distorsione complessa” = miscuglio di quella positiva e quella
negativa.
E' meno comune, ma non così rara. E' una distorsione negativa
vicino al centro dell'immagine e, gradualmente, si trasforma in
una distorsione positiva ai bordi.
3/3
Aberrazioni Cromatiche
Si verificano perché l'indice di rifrazione del vetro è diverso alle
diverse lunghezze d'onda.
Dato che la lunghezza d'onda determina il colore visto
dall'occhio, questo tipo di aberrazione rende l'immagine della
stella un punto sfuocato colorato.
Esempio:la luce bianca viene
dispersa in un prisma a causa
dei diversi indici di
rifrazione dei vari colori.
1/5
Aberrazioni Cromatiche
In generale l'indice di rifrazione è una funzione della frequenza
f della luce, quindi n = n(f) o, alternativamente, rispetto alla
lunghezza d'onda n = n(λ).
La dipendenza dalla lunghezza d'onda dell'indice di rifrazione di
un materiale è solitamente quantificato mediante formule
empiriche, quale l'equazione di Cauchy.
n è l'indice di rifrazione

lambda è la lunghezza d'onda

A,B e C = coefficienti legati al tipo di materiale utilizzato.

2/5
Aberrazioni Cromatiche
Di solito è sufficiente utilizzare l'eq. di Cauchy semplificata:
dove i coefficienti A e B sono calcolati appositamente per questa
espressione.
Materiale
A
B (μm2)
Vetro di quarzo
1.4580
0.00354
Vetro borosilicato BK7
1.5046
0.00420
Vetro crown duro K5
1.5220
0.00459
Vetro crown con Bario BaK4
1.5690
0.00531
Vetro flint con Bario BaF10
1.6700
0.00743
Vetro flint denso SF10
1.7280
0.01342
3/5
Aberrazioni Cromatiche
Gli indici di rifrazione, dunque, aumentano al diminuire della
lunghezza d'onda.

I diversi tipi di vetro vengono forniti con i valori di indice di
rifrazione a determinate lunghezze d'onda.

Alcune di queste lunghezze d'onda sono esplicitate insieme
all'elemento chimico che le produce.

4/5
Aberrazioni Cromatiche
Esistono due tipi di aberrazioni cromatiche.
aberrazione cromatica longitudinale: chiamata anche
aberrazione cromatica assiale. Abbiamo visto che il fuoco di una
lente nei diversi colori è diverso a causa della rifrazione. La luce
blu, ad esempio, viene rifratta più intensamente rispetto a quella
rossa. Questa aberrazione può essere corretta utilizzando un
obiettivo rifrattivo.

aberrazione cromatica laterale: il fuoco dei diversi colori,
fuori dall'asse ottico, non coincide.

5/5
Aberrazioni Cromatiche
5/5
Aberrazioni Cromatiche
Esistono due tipi di aberrazioni cromatiche.
aberrazione cromatica longitudinale: chiamata anche
aberrazione cromatica assiale. Abbiamo visto che il fuoco di una
lente nei diversi colori è diverso a causa della rifrazione. La luce
blu, ad esempio, viene rifratta più intensamente rispetto a quella
rossa. Questa aberrazione può essere corretta utilizzando un
obiettivo rifrattivo.

aberrazione cromatica laterale: il fuoco dei diversi colori,
fuori dall'asse ottico, non coincide.

5/5
Aberrazioni Cromatiche
5/5
Ingrandimento e Luminosità
Dimensione dell'immagine formata nel piano focale del telescopio:
lunghezza focale (f)

dimensione dell'oggetto che si osserva.

Se d = angolo sotteso dall'oggetto
allora la dimensione sul piano focale è
l = f • tan d
Per piccoli angoli la tangente si può approssimare con il valore
dell'angolo in radianti. Valgono le seguenti relazioni:
1 rad = 57,3° = 3438'= 206265 arcsec
1/3
Ingrandimento e Luminosità
Se d”= diametro dell'oggetto in secondi, una buona
approssimazione per le dimensioni sul piano focale è data da
l = f •d”/206265.
La quantità di luce raccolta da un obbiettivo, invece, dipende
dalla sua area, cioè da
¼ • π •D2
dove D è il diametro dell'obbiettivo.
Attenzione: l'ingrandimento farà sì che la luce raccolta venga
sparsa su un'area proporzionale al quadrato della lunghezza
focale (f2).
2/3
Ingrandimento e Luminosità
Quando osserviamo al telescopio, a causa del nostro occhio,
abbiamo bisogno di un oculare (immagine virtuale del piano focale
posta all'infinito).
Anche per l'oculare vale la relazione l = f •d”/206265, che
possiamo riscrivere fo • do”/206265 (fo = focale oculare).
Dunque f •d” = fo • do”; da cui f/fo = do”/d.
do”/d = rapporto tra le dimensioni angolari dell'immagine
virtuale osservata attraverso l'oculare e le dimensioni angolari
dell'oggetto, cioè è l'ingrandimento I = (anche) f/fo.
Usando un ingrandimento più alto, l'immagine apparirà più scura,
perchè la luce verrà sparsa su un angolo maggiore. La scelta
dell'ingrandimento è quindi un compromesso che deve tenere
conto di vari fattori, non ultimo dei quali la risoluzione.
3/3
Risoluzione
Esiste un limite fisico a quanto può essere definita l'immagine.
Il limite dipende dalla natura ondulatoria della luce (propagazione
non in linea retta come nell'approssimazione dell'ottica
geometrica).
Diffrazione = quando incontra un ostacolola luce cambia in parte
direzione.
Tanto più piccolo è
l'obbiettivo, tanto più
importante diventa questo
fenomeno.
L'immagine è una figura di
diffrazione, chiamata disco di
Airy.
1/2
Risoluzione
Dimensione angolare (in arcsec) disco di Airy = 135/D
(D = diametro del telescopio, mm)
Stelle di uguale luminosità: risolte fino a che la loro distanza
rimane maggiore del potere risolutivo del telescopio (= limite di
Dawes, 120/D)
Stelle di diversa luminosità: diventa via via più difficile
separarle, perchè la luce della più debole diventa indistinguibile.
Nel caso di sistemi ad alta luminosità (obbiettivi fotografici) o di
telescopi di grandi dimensioni, il fattore che limita il potere
risolutivo non è la natura ondulatoria della luce, ma la presenza di
aberrazioni ottiche.
2/2
Lavorazione di uno specchio parabolico
A partire da un disco di vetro del diametro desiderato (che
corrisponderà al diametro del telescopio) è possibile realizzare
uno specchio parabolico.
Posizionandosi su di un banco di lavoro circolare ed utilizzando un
utensile (un disco di vetro di diametro uguale a quello che si
intende lavorare) si procede alle varie fasi della lavorazione
(sbozzatura, controllo, lucidatura).
Durante la sbozzatura viene data la giusta concavità allo
specchio (legata alla focale desiderata) sfregando lo specchio
stesso con l'utensile ed interponendo tra i due degli abrasivi di
grana via via più sottile.
Raggiunta la forma corretta, si procede alla lucidatura tramite
polvere di ossido di cerio.
Il controllo degli errori di forma dello specchio viene effettuato
1/2
tramite il test di Ronchi.
Lavorazione di uno specchio parabolico
Filmato
2/2