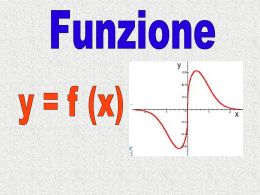
Figure sul reticolo
cartesiano
L'aggettivo cartesiano è riferito al matematico e filosofo
francese René Descartes (1596 – 1650), italianizzato
in Renato Cartesio, latinizzato in Renatus Cartesius .
L'idea di questo sistema di riferimento fu sviluppato nel
1637 in due scritti da Cartesio.
Nella seconda parte del suo Discorso sul metodo, Cartesio
introdusse la nuova idea di specificare la posizione di
un punto o di un oggetto su una superficie usando due
rette che si intersecano in un punto come strumenti di
misura.
Ogni punto del piano era collegato ad una coppia
ordinata di valori numerici: le famose coordinate, che
oggi si chiamano cartesiane. Tuttavia, poiché non
riconosceva alcun ruolo ai numeri negativi, si limitò ad
operare solo nel primo quadrante positivo.
Realizzazione a cura del Prof. Francesco Porfido
PIANO CARTESIANO
•
•
•
Per disegnare il piano
cartesiano è sufficiente
disegnare
due
rette
orientate perpendicolari fra
di loro
Di solito si disegnano le
due rette in modo che una
sia orizzontale e l’altra
verticale e il punto
d’intersezione è chiamato
origine degli assi, mentre le
due rette , assi cartesiani
La retta orizzontale è detta
asse delle ascisse o asse
delle x, la retta verticale è
detta asse delle ordinate o
asse delle y
y
0
x
PIANO CARTESIANO
•
•
•
Abbiamo così due assi
orientati (cioè con un verso
individuato da una freccia):
l'asse delle x e l'asse delle
y. Essi sono orientati da
sinistra a destra (ascisse) e
dal basso verso l'alto
(ordinate).
Scegliamo
un'unità
di
misura |-| che corrisponde
ad un'unità intera, cioè ad
1. Se usi i fogli a quadretti,
ad esempio, ti basterà
prendere come unità di
riferimento un quadretto.
Riportiamo tale unità sui
due assi
Unità di misura
Asse delle ordinate
1
y
0
x
Asse delle ascisse
PIANO CARTESIANO
•
•
•
Assegniamo
all’origine
degli assi il valore x = 0 per
l’asse delle ascisse e y = 0
per l’asse delle ordinate
Nel caso dell'asse delle x a
sinistra dello zero avremo i
numeri negativi, e a destra
i numeri positivi. Andando
da sinistra verso destra i
numeri aumentano di
valore.
Per l'asse delle y avremo i
numeri negativi al di sotto
dell'origine e al di sopra
dell'origine quelli positivi, e
muovendoci dal basso
verso l'alto i numeri
aumentano di valore.
1
y
8
7
6
5
4
3
2
1
-3 -2 -1 0
-1
-2
-3
1
2
3
4
5
6
7
8
x
PIANO CARTESIANO
• Ora possiamo rappresentare
un qualsiasi punto P del piano
cartesiano
mediante
una
coppia ordinata di numeri reali
• Si proietta perpendicolarmente
il punto sull’asse delle x
• Il valore 5 individuato sull’asse
delle x si chiamerà ascissa del
punto P
• Si proietta lo stesso punto
sull’asse delle y
• Il valore 6 individuato sull’asse
y si chiamerà ordinata del
punto P
• Il punto P sarà rappresentato
da una coppia di numeri
P (5,6)
Si legge: punto P di coordinate
cinque e sei
1
y
8
Ordinata di P 7
P
6
5
4
3
2
1
-3 -2 -1 0
-1
-2
-3
1
2
3
4
5
6
Ascissa di P
7
8
x
PIANO CARTESIANO
• In questo modo abbiamo un
vero e proprio sistema di
coordinate
che
da
una
parte associa ad ogni punto del
piano cartesiano una e una sola
coppia di numeri
P → (xp , xp )
• Dall'altra sappiamo che ad una
qualsiasi coppia di numeri reali
corrisponderà uno ed un solo
punto del piano
(x , y) → punto
Abbiamo realizzato così un tipo di
corrispondenza coppie-punti che
in Matematica si dice biunivoca.
I numeri della coppia che
individua il corrispondente punto
nel piano cartesiano prendono il
nome di coordinate del punto.
1
y
Ordinata di P
8
7
P (5 , 6)
6
5
Ascissa di P
4
3
2
1
-3 -2 -1 0
-1
-2
-3
1
2
3
4
5
6
7
8
x
ESEMPIO DI
RAPPRESENTAZIONE
• Dobbiamo rappresentare
seguenti punti:
A (-3 , 3 )
B (5, 6 )
C (3 , -2)
i
1
y
8
7
B (5 , 6)
6
5
• Svolgimento: ci basta disegnare
gli
assi
del
piano
cartesiano come abbiamo fatto
in
precedenza,
fissando
un'unità di misura e graduando
gli assi. Fatto ciò dobbiamo solo
segnare i punti.
• Unendo i punti otteniamo un
triangolo.
A (-3 ,3)
4
3
2
1
-3 -2 -1 0
-1
1
2
3
4
-2
-3
C (3 , -2)
5
6
7
8
x