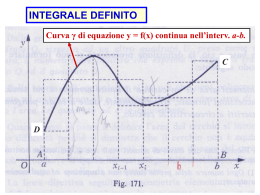
L’integrale definito di una funzione
 Il trapezoide
I plurirettangoli
 L’integrale definito di una funzione
f x   0
 L’integrale definito
 Il teorema fondamentale del calcolo integrale
 Il calcolo delle aree
Il trapezoide
Data una funzione f (x) continua
e positiva (o nulla) nell’intervallo
[a; b], si chiama trapezoide
la figura piana delimitata
dall’asse x, dalle rette y = a , y = b
e dal grafico della funzione f
nell’intervallo.
Indichiamo con S l’area del
trapezoide.
I plurirettangoli
 Dividiamo l’intervallo [a; b] in n
parti uguali (per es. n = 3).
 Per ogni intervallo consideriamo il
minimo e il massimo della funzione e
costruiamo il rettangolo corrispondente.
Si ottengono due plurirettangoli di aree
sn e S n con: sn  S  Sn .
 Le superfici sn e S n costituiscono
una approssimazione per difetto e
per eccesso dell’area S del trapezoide.
 Se aumentiamo il numero di suddivisioni n, le aree
approssimano sempre meglio l’area S del trapezoide.
Plurirettangolo con n = 6
sn e S n
Plurirettangolo con n = 12
L’integrale definito
 f  x   0
Data una funzione f (x) continua
e positiva (o nulla) nell’intervallo
[a; b] , si chiama integrale definito,
e si indica con
 f x  dx :
b
a
 f xdx  lim s
b
a
n 
n
 lim S n  S .
n 
L’integrale definito di una funzione
 Data una funzione f (x) continua
nell’intervallo [a; b],
dividiamo l’intervallo in n parti
mediante i punti x0 , x1 , ..., xn .
 Per ogni sottointervallo [ xi 1 ; xi]
scegliamo un generico punto ci :
c1 , c2 , ..., cn .
 Per ciascun intervallo [ xi 1 ; xi]
costruiamo il rettangolo di altezza
f ci  e cosideriamo la seguente
somma di aree dei rettangoli:
S  f c1   x1  ...  f xn   xn .
 Indichiamo con xmax la massima
ampiezza dei sottointervalli.
Si definisce integrale definito esteso
all’intervallo [a; b]:
 f x  dx 
b
a
lim S
xmax 0
Il teorema fondamentale
del calcolo integrale
Se una funzione f x  è continua
in [a; b], allora esiste la derivata
della funzione integrale:
F x    f t  dt
x
e vale:
a
F ' x   f x .
In particolare:
 f t  dt  F b  F a.
b
a
Il calcolo delle aree
 La funzione è positiva o al più nulla
S   f x  dx
b
a
 La funzione è almeno in parte negativa
S   f x  dx   f x  dx
b
c
a
b
 Due funzioni delimitano una superficie chiusa
(f(x)  g(x))
S    f x   g x  dx
b
a