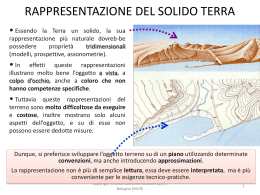
Iniziamo con la rappresentazione
dell’architettura…
Z
X
Y
… e se l’edifico è complesso?
Abbiamo quindi 2 problemi:
• la scelta della superficie di riferimento
GEODESIA
vediamo qual è la miglior superficie per
rappresentare la terra
• lo sviluppo sul piano di tale superficie
CARTOGRAFIA
sviluppiamo sul piano questa superficie
La rappresentazione è in prima approssimazione una
proiezione ortogonale
• in quale sistema di riferimento?
• c’è un sistema nazionale/internazionale unico?
Forma della terra
La terra è tonda e liscia come una palla da
biliardo (irregolarità dell’ordine di 1/1000)
GEOIDE
Il Geoide è quella superficie che è sempre perpendicolare alle
linee di forza del campo gravitazionale.
P
mare
verticale
q
P’
Geoide
Assumiamo il Geoide come riferimento delle quote
Quota di P è la distanza di P dal Geoide, considerata sulla vertic
v
Un po’ di storia…………..

A
R
S
Eratostene 220 a.c.
ipotesi: Terra sferica non animata da
moti
 verticale diretta nel centro
Come determinarne il RAGGIO?
•I raggi del Sole si considerano paralleli in quanto provenienti ~
dall’
•A Siene (S), nel giorno del Solstizio d’estate, il Sole illumina il
fondo dei
pozzi: è allo Zenit
AS=R*
•E’ possibile misurare  ad Alessandria (A)
•AS è misurato (a passi di cammello!)
Errore dell’ordine del 10% !!!
AS=R*
Copernico, Galileo, Keplero,…
Scoprirono i moti terrestri:la Terra
non è una sfera : è schiacciata
Mac Laurin (1700): ELLISSOIDE DI ROTAZIONE
c
a
  1/300
Sorse il problema di come
determinare valori per a e c, ovvero
=(a-c)/a
Campagne per la misura del grado
a diverse latitudini:
CASSINI – meridiano di Francia
PERU’ - LAPPONIA (1737-1743)
Bessel
1841
6 377 397
1/299.2
Clarke
1880
6 378 243
1/293.5
Hermert
1906
6 378 243
1/298.3
Hayford
1909
6 378 388
1/297.0
Krassowsky
1942
6 378 245
1/298.3
WGS84
(GRS80)
1988
6 378 137
1/298.257
Ellissoide
Geoide
prime
rappresentazioni
cartografiche
italiane
adottato come
ellissoide
internazionale
GPS
CONSIDERAZIONI SUL GEOIDE
z
Ogni particella della
Terra è animata nel
cosmo da un movimento
che deve essere
considerato risultante di
moti elementari.
nord
r
P
Q
y
x
sud
FORZE AGENTI SULL’ELEMENTO P
Ai fine del calcolo
della gravità è
sufficiente, per i nostri
scopi considerare il
moto di rotazione
(precessione,
nutazione, .. sono
La
velocità angolare di
ininfluenti)
rotazione  è costante e
vale  = 2p/86164 rad/sec
z nord
Attrazione newtoniana: sul
punto P, dove è concentrata la
massa m, la massa M,
concentrata 
in Q esercita
m  M la
F = G 2
forza
l
Accelerazione centrifuga:
sul punto P, dove è
concentrata la massa m, il
moto rotatorio della Terra
intorno all’asse polare
causa un’accelerazione
a = ² r, dove:
•r è la distanza del generico
punto P dall’asse di rotazione
• è la velocità angolare del
moto di rotazione (2p/giorno
siderale)
L’accelerazione determina
una forza
 centrifuga pari a:
dove:
•l è la distanza tra P e Q
•G costante newtoniana 6.67 10-11
m3kg-1s-2
massima all’equatore, nulla ai
poli
rP
P f
r
Q
y
F
g
x
su
d
f = ma = m 2 r
Non possiamo calcolare con la formula F=(G M m’)/l² l’attrazione che
TUTTA LA TERRA esercita su P
Decomponiamo la massa in elementi infinitesimi dM
Ciascun elemento infinitesimo esercita sul punto P
dF = G dM
l2
La risultante F di tutte le forze
elementari è l’attrazione newtoniana esercitata da tutta la Terra su P
Pf
d
F
g
Su P agiscono in prima
approssimazione f, dovuta al moto
rotatorio, dF, dovuta all’attrazione
newtoniana. Cioè
g= dF +f La forza di gravità g è
di
g è la forzalaqueste
dicomposizione
gravità
due forze
Ogni punto della Terra è soggetto alla forza di gravità ed ha
un suo valore di g
La gravità costituisce un campo di forze: IL CAMPO
GRAVITAZIONALE
POSSIAMO CONSIDEARE LE LINEE DI FORZA DEL CAMPO
GRAVITAZIONALE
e cioè
LINEE CHE HANNO IN OGNI LORO PUNTO PER TANGENTE LA
DIREZIONE DELLA FORZA
Le linee di forza del campo gravitazionale sono curve gobbe e
si chiamano verticali
La tangente alla loro direzione in un
punto è fornita dal filo a piombo: è
facilmente individuabile
geoide
Siamo arrivati a dire che:
•esiste un campo di forze, il campo gravitazionale
•le linee di forza del campo gravitazionale sono inviluppate
dalle verticali
dm in P sia unitaria,
dm=1
z nord
P
Q
c
b
x
y
dM
a
g = dF + f
P f
r
F
z
x
g
y
dM
dF = - G (x-a)² + (y-b)² + (z-c)²
sud
f = ² r = ² (x² + y²)½
Quando si dice che una funzione v =v(x,y,z) ammette un
potenziale (x,y,z) ?
Quando
 = vx
x
 = vy  = vz
y
z
Le due funzioni dF e f ammettono come potenziali dV e v
dm
dV = G [(x-a)² + (y-b)² + (z-c)² ] ½
=G
dm
l
v = 1² (x² + y²) = 1 ² r²
2
2
Per i potenziali vale la proprietà additiva
 da db dc
V = G 
½
[(x-a)²
+
(y-b)²
+
(z-c)²
]

dm volume elementar
 densità
a b c variabili di
integrazione
IL POTENZIALE DELLA GRAVITÀ
W(x, y, z) = V (x, y, z) + v (x, y)
Ponendo
W(x, y, z) = cost
Troviamo l’equazione
di una superficie il cui potenziale ha valore costante,
cioè
Linee di forza
UNA SUPERFICIE EQUIPOTENZIALE
Facendo variare la costante
in W= ci
si ottiene UNA FAMIGLIA DI SUPERFICI,
superfici di livello,
che in ogni loro punto sono normali W=
alla direzione della
gravità
ci
Quella particolare superficie
di livello che passa per un
punto stabilito, e che
definisce il livello medio del
mare, è il GEOIDE
P
mare
GEOIDE
P’
Linee di forza
W=
ci
verticale
W=c0
W(x, y, z) = V (x, y, z) + v (x, y) = C
linea di forza
la verticale
le è tangente
g
g è la forza di gravità
W(x, y, z) = G   da db dc
½
 [(x-a)² + (y-b)² + (z-c)² ]
+ 1 ² r²
2
IL GEOIDE È L’ESPRESSIONE MATEMATICA DELLA TERRA
W(x, y, z) = G   da db dc
½
[(x-a)²
+
(y-b)²
+
(z-c)²
]

+ 1 ² r²
2
IL GEOIDE È L’ESPRESSIONE MATEMATICA DELLA TERRA
PERCHE’ NON UTILIZZIAMO L’ESPRESSIONE DEL
GEOIDE NEL PASSAGGIO
superficie fisica della Te
GEOIDE
PROIEZIONE SUL PIANO
W(x, y, z) = G   da db dc
½
 [(x-a)² + (y-b)² + (z-c)² ]
+ 1 ² r²
2
QUESTA FORMULA NON E’ OPERATIVA PERCHE’
NON CONOSCIAMO IL VALORE DI

superficie fisica della Terr
GEOID
E
ELLISSOIDE
PROIEZIONE SUL PIANO
A Torino differenza di ca. 50 m
A Torino scostamento di circa 50m
SISTEMI ASSOLUTI E RELATIVI
Coordinate geografiche (dipendono dal datum)
Latitudine ()
 Paralleli
Longitudine ()
 Meridiani
Z
Meridiano
Parallelo
Normale
P

Y

X
Geodetica: curva gobba di minima
lunghezza che unisce due punti
sull'ellissoide ( distanza)
Q
y

x
P
s
O
Coordinate geodetiche polari e rettangolari
sfera osculatrice
Z
Normale
R= N
P
Y
Raggi principali di curvatura , N
X
Teoremi della geodesia operativa
Formule di Puiseaux-Weingarten
Q
Fino a lunghezze di archi di geodetica
dell'ordine del centinaio di
chilometri:
A
sez. normale
•

P
geodetica
O
•
gli angoli misurati fra sezioni
normali (A) differiscono da quelli
delle corrispondenti geodetiche ()
di quantità sicuramente inferiori
alla massima precisione possibile
nelle misure angolari
la differenza di lunghezza fra un
arco misurato di sezione normale
ed il corrispondente arco di
geodetica è sempre trascurabile
per qualsiasi valore della
lunghezza dell'arco medesimo
Semplificazioni della superficie di
riferimento
Z
X
A

tang alla geodetica
O
P2
sfera locale
ellissoide
Y
P1
Scostamenti ellissoide-sfera - PLANIMETRIA
s (km)
50
100
150
200
x (mm)
3.47
27.74
93.62
226.35
0.07 10-6
0.28 10-6
0.62 10-6
1.13 10-6
x/s
Campo geodetico (di Weingarten)
Precisione 10-6
Scostamenti ellissoide-sfera - ALTIMETRIA
1
10
20
50
100
0.03
2.66
10.63
66.43
265.72
S (km)
z (cm)
Livellazione trigonom.
Scostamenti ellissoide-piano - PLANIMETRIA
s (km)
1
10
15
30
50
x (mm)
0.004
4
14
112
519
0.004 10-6
0.4 10-6
0.9 10-6
3.7 10-6
10.4 106
x/s
Precisione 10-6
Campo topografico
Scostamenti ellissoide-piano - ALTIMETRIA
s (km)
0.1
0.5
1
10
15
z (cm)
0.08
2.0
7.9
789
1775
Livellazione geom.