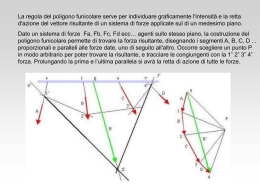
ANGOLI
ORIENTATI
DEFINIZIONE CLASSICA DI ANGOLO
L’angolo è la porzione di piano contenuta tra due semirette
con la stessa origine.
A
- L’origine comune O è detta vertice.
- Le due semirette OA = a e OB = b
sono dette lati.
a

O
b
?
- L’angolo viene indicato con la
notazione AOB, oppure con una
lettera minuscola dell’alfabeto greco,
per es. , , .
B
AOB
Questa semplice definizione, tuttavia, contiene un’ambiguità. Essa non
definisce quale delle due porzioni di piano è l’angolo a cui ci si riferisce.
Per eliminare questa ambiguità, occorre introdurre il concetto di:
angolo orientato
Copyright © 2009 Zanichelli editore S.p.A., Bologna [6629]
2
ANGOLO ORIENTATO
Immaginando di far ruotare attorno al vertice O la semiretta a, partendo dalla
posizione iniziale OA assunta come origine, fino a fermarla nella posizione finale OB,
essa descrive una porzione di piano costituente l’angolo AOB.
La semiretta a può ruotare intorno a O in due sensi opposti per andare a
sovrapporsi a quella b: in senso orario, oppure in senso antiorario. Si conviene di
considerare positivo il senso orario, negativo quello antiorario.
A
- OA = a è detto lato origine.
- OB = b è detto lato estremo.
a
O
- La rotazione oraria definisce
l’angolo positivo AOB = .

+
-
b
B
- Nella notazione AOB, AO
rappresenta il lato origine, OB
quello estremo.
Se la semiretta origine a ruota intorno a O in senso antiorario, essa
descrive una diversa porzione di piano che costituisce l’angolo  negativo.
Copyright © 2009 Zanichelli editore S.p.A., Bologna [6629]
3
ANGOLO ORIENTATO
In questo modo viene eliminata l’ambiguità implicita nella definizione di angolo
L’angolo AOB =  è la parte di piano individuata dalla rotazione positiva di AO per
sovrapporsi su OB.
L’angolo BOA =  è la parte di piano individuata dalla rotazione positiva di BO per
sovrapporsi su OA.
A
a

O

b
B
Se il lato origine OA dell’angolo AOB va a sovrapporsi al lato estremo OB dopo
aver decritto uno o più angoli giri completi, si ottiene un angolo con ampiezza
maggiore dell’angolo giro.
Copyright © 2009 Zanichelli editore S.p.A., Bologna [6629]
4
IL RADIANTE
Gli angoli sono grandezze misurabili. Per misurare un angolo occorre in primo
luogo fissarne l’unità di misura.
In matematica, l’unità di misura è il radiante. Esso è definito come l’angolo al
centro di una circonferenza che sottende un arco di lunghezza uguale al suo raggio.
A

rad
R

O
R
Per l = R si ha:
l
B
R
 1rad
R
R
ANGOLO GIRO
ANGOLO PIATTO
l

R
ANGOLO RETTO
2R
R
R

rad
rad
----- = 2 = 6 ,28318… ----- =  = 3 ,14159… ----- = ------ = 1rad,57079…
R
R
2R
2
l
 rad
l  R   rad
Copyright © 2009 Zanichelli editore S.p.A., Bologna [6629]
5
UNITÀ DI MISURA DEGLI ANGOLI
Il radiante è congeniale a considerazioni di carattere teorico, mentre in ambito
pratico-applicativo si preferisce definire altre unità di misura degli angoli.
 Sistema sessagesimale: l’unità è il grado sessagesimale, indicato con (°) e pari a 1/90
dell'angolo retto; i suoi sottomultipli sono:
– il primo sessagesimale, (‘), 1/60 del grado,
– il secondo sessagesimale, (“), 1/60 del primo (1/3600 di grado).
Un angolo viene, quindi, indicato:  = 25° 37’ 29”.
 Sistema decimale: l’unità di misura è la stessa del precedente sistema (gradi
sessagesimali), mentre i sottomultipli sono decimi, centesimi, millesimi, ecc. di grado.
Un angolo viene quindi indicato:  = 218°,3456.
Il sistema sessagesimale viene usato per facilitare i calcoli, in quanto le operazioni aritmetiche
vengono eseguite con le familiari regole della numerazione decimale.
 Sistema centesimale: l’unità di misura [grado centesimale indicato con (c), (g) o (gon)],
vale 1/100 dell’angolo retto. I sottomultipli sono:
– il primo centesimale, (), pari a 1/100 di grado;
– il secondo centesimale, (=), pari a 1/100 di primo (1/10.000 di grado).
Un angolo viene scritto nel modo seguente:  = 78C 39 87=.
Notiamo, però, che 87= sono 87/100 di primo, quindi, 87/10000 di grado; in
conseguenza di ciò, l’angolo centesimale viene di norma scritto nel modo
seguente: 78C,3987 (dunque il sistema centesimale si presenta in forma decimale).
Copyright © 2009 Zanichelli editore S.p.A., Bologna [6629]
6
TRASFORMAZIONE
SESSAGESIMALIDECIMALI
Conversione dal sistema sessagesimale al sessadecimale
Bisogna dividere i primi per 60 e i secondi per 3600, quindi si sommano le parti
decimali ottenute al valore intero dei gradi. Consideriamo l’angolo di 48° 17’ 26”:
17’
26”
48° 17’ 26”= 48° + ---- + -------- = 48°,2905
60’
3600”
Conversione dal sistema sessadecimale al sessagesimale
Per eseguire questa conversione bisognerà moltiplicare per 60 la frazione di grado e la
frazione di primi. Consideriamo l’angolo 48°,2905.
0°,2905  60 = 17’,43
0’,43  60 = 26”
per cui sarà 48° 17’ 26”.
Copyright © 2009 Zanichelli editore S.p.A., Bologna [6629]
7
TRASFORMAZIONE SESSAG.RADIANTI
L’ampiezza degli angoli rimane invariata, qualunque unità di misura si utilizzi; dunque
l’angolo piatto espresso in radianti è equivalente all’angolo piatto espresso in gradi sess.
 rad



180
Conversione dal sistema sessagesimale a radiometrico
 rad   
Esempio: ° = 142° 15’ 38” = 142°,2605 →

180
 rad  142,2605

180
 2rad ,4829
Conversione dal sistema radiometrico a sessagesimale
  
Esempio: rad = 1rad,0000
→
rad
180

 o  1rad ,0000
180

 57,2958  5717'44",8
Copyright © 2009 Zanichelli editore S.p.A., Bologna [6629]
8
TRASFORMAZIONE
CENTESIMALERADIANTI
 rad
c


200c
Conversione dal sistema centesimale a radiometrico
 rad 
Esempio:
c =
275c,7615
→
c
200
c


rad
275c ,7615

  4rad ,3316
200
Conversione dal sistema radiometrico a centesimale
rad

c 
200c

Esempio:
rad =
3rad,7720
→
 
c
3rad ,7720

200  240c ,1330
Copyright © 2009 Zanichelli editore S.p.A., Bologna [6629]
9
TRASFORMAZIONE
CENTESIMALESESSAGESIMALE

180

c
200c
Conversione dal sistema centesimale a sessagesimale
   c
Esempio:
c =
78c,8412
180
9
c
200
10
78c ,8412
 
180  70,9571  7057'25",5
200
→
Conversione dal sistema sessagesimale a centesimale
200
10
  
 
180
9
c
Esempio: ° = 68° 21’ 00” = 68°,3500
→
 c  68,3500
10
 75c ,9444
9
Copyright © 2009 Zanichelli editore S.p.A., Bologna [6629]
10
TRASFORMAZIONE ANGOLI PICCOLI
Talvolta è necessario convertire in radianti un angolo in forma sessagesimale
espresso in secondi (perché molto piccolo); in questo caso può risultare comodo
esprimere in secondi anche l’angolo piatto:
 "   rad

rad
180  3600

 "
  rad  206265

180  3600

"
206265
Per convertire in radianti un piccolo angolo espresso in secondi centesimali
(poco usato per la praticità dei gradi centesimali)
 

rad
200 10000
 rad   

  rad  636620

200 10000


636620
Copyright © 2009 Zanichelli editore S.p.A., Bologna [6629]
11